КРАТКИЙ ТЕОРЕТИЧЕСКИЙ СПРАВОЧНИК.
Треугольники.
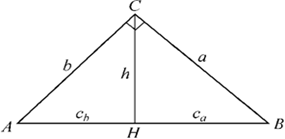
Прямоугольный треугольник.
Метрические соотношения.
;
;
; 
;
,
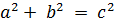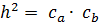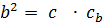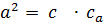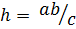где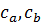 
- проекции катетов 
, 
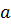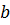на гипотенузу 
; 
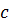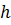-высота.
Соотношения между сторонами и углами.
sin A = 
; tg A = 
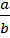; cos A = 
; ctg A = 
;
Формулы для вычисления радиусов вписанной ( r ) и описанной ( R ) окружностей.
R =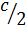 
= m; r = 
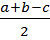, m –медиана, проведённая из вершины прямого угла .
Формула площади. S =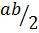 
.
Произвольный треугольник.
Определение вида треугольника по его сторонам:
- если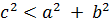 
, то треугольник остроугольный;
- если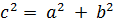 
, то треугольник прямоугольный;
- если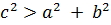 
, то треугольник тупоугольный; где c –наибольшая сторона
Соотношения между сторонами и углами.
1. Сумма внутренних углов треугольника равна 180 
.
2. Сумма двух сторон треугольника больше его третьей стороны (неравенство треугольника).
3. Против большей стороны треугольника лежит больший угол и,наоборот, против большего угла лежит большая сторона.
4. a 2 = b 2 + c 2 – 2 bc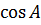 
(теорема косинусов).
5. 
= 
= 
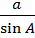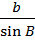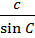= 2 R (теорема синусов).
Свойства медиан.
1. Медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
2. Медиана треугольника делит его на два равновеликих треугольника
3. Три медианы треугольника делят его на шесть равновеликих треугольников.
4. m =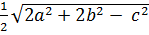 
, где m – медиана, проведённая к стороне с.
Свойства биссектрис.
1. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности вписанной в треугольник.
2. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Свойство высот.
Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Свойство серединных перпендикуляров.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
Свойства средней линии треугольника.
1. Средняя линия треугольника параллельна стороне треугольника и равна её половине.
2. Средняя линия треугольника делит пополам любой отрезок, соединяющий вершину треугольника с какой-либо точкой основания.
Формулы для вычисления площади.
1. S =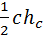 
;
2. S =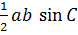 
;
3. S =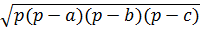 
где p - полупериметр(формула Герона);
4. S =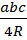 
, где R – радиус описанной окружности;
5. S = pr , где r – радиус вписанной окружности.
Формулы для вычисления радиусов вписанной ( r ) и описанной ( R ) окружностей.
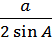R =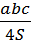 
, R = 
, r = 
.
Четырёхугольники.
Произвольный выпуклый четырёхугольник.
Вписанная окружность.
В четырёхугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны. Центром вписанной окружности является точка пересечения биссектрис.
Описанная окружность.
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180 . Центром описанной окружности является точкапересечения серединных перпендикуляров к сторонам четырёхугольника.
Параллелограмм.
Трапеция.
Правильные многоугольники.
an = 2Rn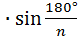 
; an = 2rn 
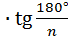; rn = Rn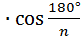 
где an – сторона правильного n -угольника, а rn и Rn – радиусы вписанной и описанной окружностей.
Окружность и круг.
Свойства хорд окружности.
Произведения длин отрезков хорд АВ и С D окружности, пересекающихся в точке Е, равны, то есть АЕ 
ЕВ = СЕ Е D .
КРАТКИЙ ТЕОРЕТИЧЕСКИЙ СПРАВОЧНИК.
Треугольники.
Прямоугольный треугольник.
Метрические соотношения.
;
;
; ;
,
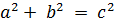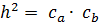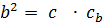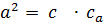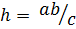где 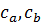- проекции катетов 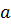, 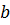на гипотенузу 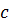; 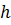-высота.
Дата: 2019-07-24, просмотров: 266.
