Алгоритм построения матриц отношений сходства и включения. Этот алгоритм отличается для указанных двух мер лишь методом расчета значений матриц сходства и включения.
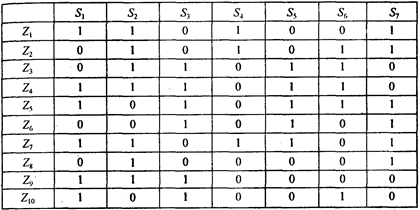
Шаг 1. Формируются два множества: множество исследуемых объектов J = { S 1, S 2,..., Sq } и множество признаков Z = { Z 1, Z 2 ,..., Zp}. Каждый объект Si описывается подмножеством признаков {Z i } Î Z, являющимся качественным признаковым образом. Все образы объектов систематизируются в матрицу образов, где представляются индексированными множествами (табл. 5.5).
Шаг 2. Генерируются все парные сочетания объектов, и для каждой пары описаний объектов Si и S j строится индексная матрица В = ║ xij ║; i = 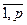 ; j =
; j = 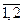 ; где р — число строк матрицы образов, соответствующее числу рассматриваемых признаков m ( Z ). На основе индексной матрицы рассчитываются меры сходства C ( Si , Sj ) или включения W ( Si, Sj). Для определения меры сходства может быть использована одна из формул, приведенных в табл. 5.4. Расчет мер включения осуществляется по формулам (5.5).
; где р — число строк матрицы образов, соответствующее числу рассматриваемых признаков m ( Z ). На основе индексной матрицы рассчитываются меры сходства C ( Si , Sj ) или включения W ( Si, Sj). Для определения меры сходства может быть использована одна из формул, приведенных в табл. 5.4. Расчет мер включения осуществляется по формулам (5.5).
Таблица 5.5
Пример матрицы образов
Например, для пары объектов S 1 и S 2 (см. табл. 5.5) меры сходства и включения имеют следующие значения:
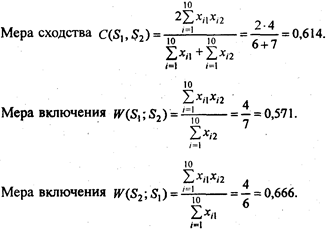
Шаг 3. На основе рассчитанных на шаге 2 значений мер сходства и включения (см. табл. 5.5) строятся соответствующие матрицы размерностью q x q (табл. 5.6, 5.7).
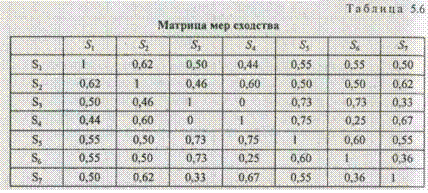
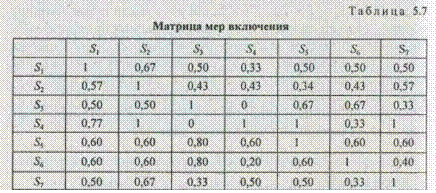
Матрица мер сходства симметрична относительно главной диагонали, а матрица мер включения таким свойством в общем случае не обладает. В приведенной матрице включения число 0,57 (первый столбец и вторая строка) соответствует W ( S 1 ; S 2 ), а число 0,67 (второй столбец и первая строка) соответствует W ( S 2 , S 1 ). Таким образом, индекс при названии первого множества в скобках указывает номер столбца, а второго — номер строки матрицы включения. При построении матрицы сходства индекс при первом множестве в мере сходства указывает номер строки матрицы, а при втором — номер столбца.
Шаг 4. Задается отношение сходства или включения в следующем виде:
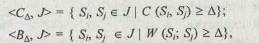
где Δ — произвольное число (0 £ Δ £ 1,0); i , j Î J .
Для заданного значения Δ строится матрица сходства [СΔ] или включения [B Δ], в которой все значения, большие или равные Δ, заменяются единицами, а оставшиеся — нулями.
Примеры матриц [С0,60] и [B 0,67] Для значений Δ ³ 0,60 и Δ ³ 0,67 приведены в табл. 5.8, 5.9.
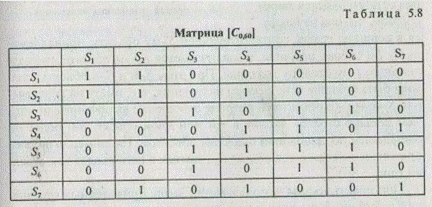
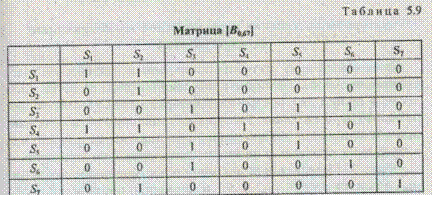
Матрицы [С0,60] и [B 0,67] отображены соответственно графами и орграфами отношений сходства и включений (рис 5.3). Дуги и стрелки соединяют те объекты, которые имеют единицу на пересечении соответствующих строк и столбцов матриц.
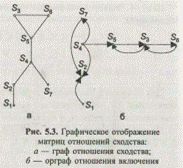
Направление стрелки в графе отношений включения устанавливается таким образом, что она начинается в вершине графа, соответствующей Si-му объекту, принадлежащему i-й строке матрицы, и заканчивается в Sj -м объекте, принадлежащем j-му столбцу матрицы. При этом Si-й и Sj-й объекты должны быть связаны отношением включения, т. е. иметь на пересечении Si-го и Sj-го объектов в матрице отношений включения единицу. Чем больше стрелок входит в тот или иной объект, тем более он оригинален по сравнению с другим объектом. Например, наиболее оригинальным является объект S 2, так как в него входят три стрелки (рис. 5.3б).
При практическом использовании выше приведенных отношений величину Δ находят путем перебора серии значений, добиваясь при этом установления всех существенных связей.
Дата: 2019-04-23, просмотров: 369.