| S1 | S2 | S3 | … | Sq | |
| Z1 | 0 | 1 | 0 | … | 1 |
| Z2 | 1 | 1 | 0 | … | 1 |
| Z 3 | 1 | 1 | 1 | … | 0 |
| … | … | ... | ... | … | … |
| Zp | 0 | 0 | 0 | 0 | 0 |
Семейство множеств S или Z с заданными на них отношениями можно рассматривать как системы, в которых связи между элементами образуют определенную структуру. Следовательно, содержание задач по обработке матриц образов систем включает подбор типов отношений и анализ структуры порождаемых ими систем.
Рассмотрим основные меры, порождающие отношения на множестве исследуемых систем.
Меры сходства и различия. Мерой сходства (близости) обычно называется величина С ( S j , S k), имеющая предел и возрастающая с возрастанием близости объектов. Под мерой сходства будем понимать неотрицательную вещественную функцию С (Sj, Sk), обладающую следующими свойствами:
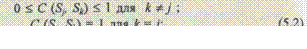
Здесь Sj , Sk — множества значений признаков, описывающие сравниваемые объекты. Мера, коэквивалентная мере сходства, называется мерой различия D ( Sj , Sk ) и обладает свойствами метрики, если:

Свойствами (5.2) обладает, в частности, континуум эквивалентных мер, представляемых формулой
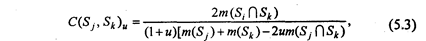
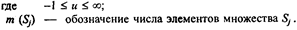
Меры сходства и различия "изобретаются" по специальным правилам [4], а выбор конкретных мер зависит, в первую очередь, от суперзадачи — цели конкретного исследования, а также от шкалы измерений. В табл. 5.4 приведены наиболее распространенные меры сходства и различия для различных значений коэффициента и (5.3), предназначенные для обработки качественных и количественных признаков.

Вычисление значений меры сходства двух сравниваемых объектов по качественным признакам удобно производить на основе бинарной матрицы, которая в терминах теории множеств задается следующим образом:

Здесь S — индексированное множество с элементами Sj (алфавит описаний), Sj — j - e описание объекта; Z — индексированное множество с элементами Z i (алфавит признаков или значений признаков); Z i — i-й признак (значение признака); xiy — одно из двух значений {0, 1} i-гo признака y j-го объекта ( xij = 1, если i-й признак есть у j-го объекта, в противном случае xij = 0); J и I— индексные множества.
Бинарная матрица для вычисления меры сходства между двумя объектами имеет следующий вид:

Вычисление меры сходства, например, по формуле Чекановского — Серенсена (см. табл. 5.4) с учетом бинарной матрицы (5.4) осуществляется по следующему выражению:
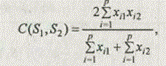
где xi 1 , xi 2 — одно из двух значений {0, 1).
Рассмотрим правила вычисления количества элементов некоторых множеств, получаемых в результате операций над ними. Количество элементов множества S равно
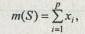
где р — общее число элементов множества S;
xi — значение i-ro элемента множества S, при этом 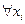 Î S ® xi = 1.
Î S ® xi = 1.
Количество элементов пересечения двух множеств S 1 Ç S 2 равно
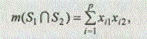
где xi 1 , xi 2 — соответственно значения i-го элемента для множеств S1 и S 2 .
Количество элементов объединения двух множеств S 1 È S 2 равно
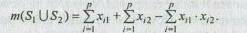
Мера включения. Она отражает различную степень включения одного объекта в другой и позволяет выявить, какой из двух сравниваемых объектов содержит больше специфических признаков, т. е. определить, какой объект более оригинален, а какой — более типичен среди множества анализируемых объектов.
Меры включения множества S 2 в множество S 1 и S 1 в S 2 определяются следующим образом:
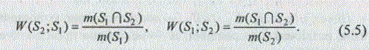
Меры включения несимметричны, а включение j-го описания в самом себе стопроцентно, так как
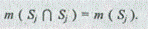
Для более полного анализа множеств исследуемых объектов рассчитываются меры сходства, различия и включения для всех пар объектов. Полученные после вычислений значения соответствующих мер сводятся в квадратные матрицы порядка q x g, номерами строк и столбцов которых являются номера изучаемых объектов.
Дата: 2019-04-23, просмотров: 348.