При определении желаемых сценариев для ситуаций, в которых процесс планирования осуществляется одним актором, следует придерживаться следующих стратегий.
В соответствии с первой стратегией проводится построение новой иерархической системы, отличающейся полностью или частично от иерархии предыдущего прямого процесса. Альтернативы в новой иерархии остаются прежними, т. е. они не изменяются по сравнению с предыдущей итерацией процесса. Во вновь формируемую иерархию включают элементы, характеризующие желаемые цели, критерии, политики, и устанавливают их относительную степень предпочтения. Изменению подвергаются также матрицы попарных сравнений альтернатив, при заполнении которых эксперту следует ответить на вопросы: Какая альтернатива из двух сравниваемых более желательна по рассматриваемому критерию? Насколько одна из альтернатив предпочтительнее другой по девятибалльной шкале (см. табл. 2.1)? Результатом реализации первой стратегии является нормализованный вектор приоритетов желаемых сценариев, рассчитанный относительно фокуса иерархии.
Вторая стратегия предполагает определение желаемых сценариев по результатам оценки выгод и издержек, которые ожидаются от реализации каждого сценария (исхода). Для решения этой задачи строятся две иерархии, по которым оцениваются относительные выгоды и издержки сценариев. В иерархиях используются все альтернативы-сценарии из предыдущей итерации прямого процесса планирования. При построении и заполнении матриц попарных сравнений альтернатив следует дать ответы на следующие вопросы: Какая из двух сравниваемых альтернатив предпочтительнее и насколько предпочтительнее относительно получения от ее реализации функциональных, экономических, социальных и других выгод (для первой иерархии) и издержек (для второй иерархии)? Результатом проведения второй стратегии первоначально является ненормированный вектор приоритетов альтернатив, рассчитанный по критерию, характеризующему отношение значений ненормированных векторов приоритетов, отражающих выгоды и издержки. Затем ненормированный вектор приводится к нормированному (табл. 3.3) и далее используется в очередном процессе планирования.
Таблица 3.3
Нормирование вектора приоритетов
| Альтернатива-исход (А,) | A1 | А 2 | A3 |
| Вектор приоритетов выгод | 0,5 | 0,3 | 0,2 |
| Вектор приоритетов издержек | 0,2 | 0,3 | 0,5 |
| Ненормированный вектор приоритетов отношений выгод и издержек | 2,5 | 1,0 | 0,4 |
| Нормированный вектор приоритетов отношений выгод и издержек | 0,64 | 0,25 | 0,11 |
Третья стратегия предполагает использование иерархии предыдущего прямого процесса и относящихся к этой иерархии матриц попарных сравнений альтернатив-сценариев со значениями экспертных оценок. Изменению в данном случае подлежат весовые коэффициенты элементов иерархических уровней, кроме уровня альтернатив. При этом весовые коэффициенты будут отражать не наиболее или наименее вероятную их значимость в будущем, как в прямом процессе, а наиболее или наименее желаемую значимость. Уровень акторов из иерархии исключается. Результатом реализации третьей стратегии является нормированный вектор приоритетов альтернатив-исходов относительно фокуса видоизмененной иерархии.
Четвертая стратегия основана на определении приоритета желаемых сценариев по результатам оценки предполагаемых последствий от реализации каждого рассматриваемого сценария. Оценка последствий осуществляется на матрице специального вида. Наименованиями строк матрицы являются критерии (Ki), характеризующие будущие важные характеристики исследуемой системы, а наименованиями столбцов — сценарии (А i ), взятые из предыдущего прямого процесса. На пересечении строк и столбцов экспертом в матрице зафиксированы оценки (aij), значения которых определены шкалой разностей (см. табл. 3.2). Для каждого сценария по матрице рассчитывается интегральная оценка ОА j
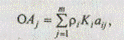
где р, — весовой коэффициент критерия К, ( i = \,т).
На основании полученной информации об интегральных оценках ОА j по каждому сценарию эксперт определяет степень важности желаемых сценариев методом попарных сравнений. При заполнении матриц попарных сравнений предпочтение отдается тем альтернативам, которые имеют большее абсолютное значение интегральной оценки OAj . Пример перехода от интегральных оценок сценариев к их вектору приоритетов приведен ниже (табл. 3.4).
Таблица 3.4
Анализ сценариев
| Альтернатива-сценарий (А j ) | А 1 | A2 | A3 | A 4 | A 5 |
| Интегральная оценка альтернативы OAj | -0,2 | 0 | -2,1 | +0,5 | +5,0 |
| Вектор приоритета альтернативы WAj | 0,03 | 0,10 | 0,02 | 0,25 | 0,6 |
Дата: 2019-04-23, просмотров: 333.