Во второй модификации рассматривается метод сравнения объектов относительно стандартов. Метод попарного сравнения альтернатив не всегда может быть эффективно применен в некоторых практических ситуациях:

• эксперту может быть предложено для анализа более девяти альтернатив. В этом случае построение однородных матриц попарных сравнений становится затруднительным. Это связано с физическими ограничениями интеллекта человека;

• при добавлении новых альтернатив изменяется порядок ранее прошедших сравнение альтернатив относительно критериев качества. Нарушение порядка альтернатив нежелательно при решении ряда прикладных задач, связанных со значительными финансовыми, материальными и социальными затратами на корректировку последствий принимаемых решений или возможностью возникновения конфликтной ситуации между экспертами, готовящими и обосновывающими решения, и лицами, принимающими решения, несущими ответственность за принятые решения и их последствия;

• альтернативы могут поступать эксперту для сравнения не одновременно, а через определенные промежутки времени. Поэтому в данной ситуации не представляется возможным попарно сравнить объекты.

Для решения проблемы сравнения и оценки альтернатив в указанных ситуациях наиболее целесообразен метод сравнения альтернатив относительно стандартов. Стандарт устанавливает уровень качества объекта относительно критерия качества. Например, критерию "надежность" для объекта "автомобиль" может быть назначено три стандарта, характеризующих соответственно высокий (H — high), средний (М — medium), низкий (L — little) уровень надежности. Каждый стандарт отождествляется, как правило, с некоторым существующим на практике эталоном качества. В качестве таких эталонов принимаются объекты, аналогичные сравниваемым альтернативам. Например, для видов обеспечения банковских кредитов высокий, средний и низкий стандарты по критерию "ликвидность" могут быть отождествлены соответственно с драгоценными металлами, ценными бумагами и недвижимостью.

В иерархической структуре стандарты присваиваются элементам, имеющим непосредственную связь с альтернативами. При этом число стандартов по каждому такому элементу (критерию качества) может быть различно и определяется экспертом с учетом конкретной ситуации. По каждому стандарту экспертом устанавливается относительная степень предпочтения, которая указывает значимость стандарта для эксперта. Численное значение каждого стандарта определяется их попарным сравнением по девятибалльной шкале (см. табл. 2.1) путем обработки матрицы

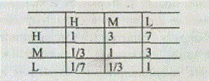
Вектор приоритетов стандартов будет иметь следующий вид:

{Н= 0,625 М= 0,257 L= 0,091}^T

Из вышеприведенной матрицы следует, что эксперт отдал слабое предпочтение высокому стандарту (Н) перед средним (М), а также среднему перед низким стандартом (L). В то же время предпочтение высокого стандарта (Н) перед низким (L) определено как очень сильное (оценка 7 в матрице).

Рассмотрим правила построения иерархии (рис. 2.6), учитывающей стандарты и алгоритм вычисления векторов приоритетов альтернатив.

Введем следующие обозначения:

С = {С₀, C_g} — множество стандартов, включающее два подмножества, устанавливающие соответственно основную { С₀ } и дополнительную { С_g } шкалы. Основная шкала включает градации С₀ ⁼ {Н, М, L}, где Н, М, L — соответственно высокий, средний и низкий уровень стандартов по определенному критерию. Дополнительная шкала может включать градации C _g = {НН, НМ, ML, LL}, где НН, НМ, ML, LL — соответственно очень высокое; промежуточное между высоким и средним; промежуточное между средним и низким; очень низкое значение стандартов.

Для конкретного элемента E^s_j , включенного в иерархию из множества С, определяется подмножество стандартов С_j, такое, что С_j Ì С, С_j Î E^s_j . Например, для элементов иерархии (см. рис. 2.6)

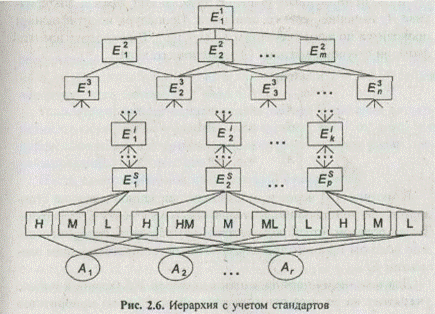
E₁^s и E^s_p  определены стандарты Н, М, L, а для элемента Е₂^s — стандарты Н, НМ, М, ML, L. Следует отметить, что экспертом могут быть назначены различные значения для одних и тех же по наименованию стандартов, относящихся соответственно к элементам E₁^s и E^s_p .

Вычисление векторов приоритетов альтернатив относительно элементов иерархии,, учитывающей стандарты, осуществляется следующим образом.

Для каждого элемента E^s_j иерархии, непосредственно связанного со стандартами, устанавливается подмножество С _j Ì С. Стандарты, входящие в подмножества С _j, сформированные относительно E^s_j , попарно сравниваются по девятибалльной шкале предпочтений. Относительные предпочтения стандартов фиксируются в матрицах, обработка которых по итерационному алгоритму, выполняемому в соответствии с соотношениями (2.2) и (2.3), позволяет определить для них правые собственные векторы W^s_j Î E^s_j . В собственном векторе верхний индекс указывает на принадлежность вектора уровню стандартов в иерархии.

Лицо, принимающее решение, присваивает каждой альтернативе А _i значение одного стандарта. Процедура идентификации проводится по всем элементам E^s_j (j = 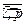). В результате идентификации строится матрица [А] следующего вида:

В матрице [А] через w_ij обозначено численное значение стандартов, соответствующее альтернативе А _i и элементу E^s_j иерархии. Таким образом, столбцы в матрице [А] образуют ненормированные векторы приоритетов альтернатив по соответствующим элементам E^s_j .

Для получения нормированных векторов W^A_j (верхний индекс указывает на то, что ранжируются альтернативы) приоритетов альтернатив матрица [А] умножается на диагональную матрицу [S] вида:

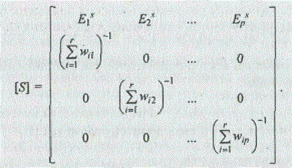
Множество нормированных векторов приоритетов альтернатив относительно всех элементов самого нижнего уровня иерархии определяется перемножением матриц

[ W^A ]=[ A ] ´ [ S ].

В полученной матрице [ W^A ] столбцами являются нормированные векторы приоритетов альтернатив W^A_j для каждого элемента E^s_j иерархии.

Дальнейшее определение векторов приоритетов альтернатив относительно элементов Eⁱ_j иерархии, расположенных выше уровня S , осуществляется в соответствии с шагами 2 и 3 алгоритма иерархического синтеза (см. разд. 2.3).

Рассмотрим пример использования метода сравнения альтернатив относительно стандартов, подтверждающий тот факт, что добавление новой альтернативы не нарушает порядок ранее проранжированных альтернатив.

Пусть имеется матрица предпочтений стандартов:

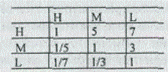
Вектор приоритетов стандартов имеет следующий вид:

Н = 0,696 М = 0,225 L = 0,079.

Рассмотрим четыре альтернативы А₁,..., А₄ которым поставлены в соответствие следующие значения вектора приоритетов стандартов:

А₁ = 0,225 (М), А₂ = 0,079 (L), А₃ = 0,225 (М), А₄ =0,079 (L),

Нормированный вектор приоритетов рассматриваемых альтернатив следующий:

А₁ А₂ А₃ А₄

W₄ = { 0,370 0,130 0,370 0,130 }^Т.

где Т — знак транспонирования;

(4) — нижний индекс, указывающий число ранжируемых альтернатив.

В соответствии с приведенным вектором альтернативы ранжируются в порядке убывания приоритета: А₁, А₃, А₂, А₄.

Добавим к рассматриваемому множеству альтернатив новую — А₅ и присвоим ей значение, соответствующее высокому стандарту — Н. Нормированный вектор приоритетов для пяти альтернатив имеет следующий вид:

А₁ А₂   А₃ А₄  A₅

W₅= {0,137 0,061 0,173 0,061 0,534}^T.

В соответствии с этим вектором альтернативы ранжируются в порядке убывания приоритета следующим образом: А₅, А₁, А₃, А₂, A₄. Анализ приведенной последовательности показывает, что добавление новой альтернативы А₅, не привело к нарушению порядка у ранее проанализированных альтернатив А₁, ..., А₄.