ВАРИАНТ 2
ЧАСТЬ 1
1. Решите уравнение 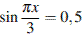 . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.
2. Материальная точка движется прямолинейно по закону 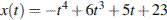 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени 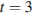 с.
с.
3. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

4. На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
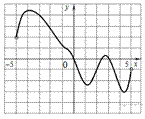
5. В прямоугольном параллелепипеде 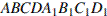 известно, что
известно, что 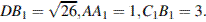 Найдите длину ребра
Найдите длину ребра 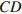 .
.
6. 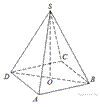 В правильной четырехугольной пирамиде
В правильной четырехугольной пирамиде 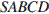 точка
точка 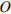 – центр основания,
– центр основания, 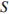 – вершина,
– вершина, 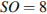 ,
, 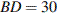 . Найдите боковое ребро
. Найдите боковое ребро 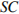 .
.
7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
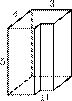
8. Найдите 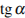 , если
, если 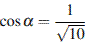 и
и 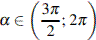 .
.
9. Найдите значение выражения 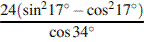
10. Небольшой мячик бросают под острым углом 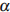 к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой
к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой 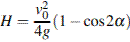 , где
, где 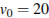 м/с – начальная скорость мячика, а
м/с – начальная скорость мячика, а 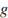 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте 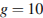 м/с
м/с 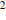 ). При каком наименьшем значении угла
). При каком наименьшем значении угла 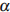 (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
(в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
11. Найдите наименьшее значение функции 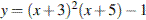 на отрезке
на отрезке 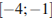
12. Найдите точку максимума функции 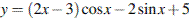 , принадлежащую промежутку
, принадлежащую промежутку 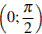
ЧАСТЬ 2
С1 а) Решите уравнение 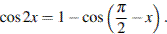
б) Найдите все корни этого уравнения, принадлежащие промежутку 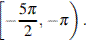
С2 Сторона основания правильной треугольной призмы 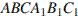 равна
равна 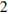 , а диагональ боковой грани равна
, а диагональ боковой грани равна 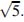 Найдите угол между плоскостью
Найдите угол между плоскостью 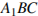 и плоскостью основания призмы.
и плоскостью основания призмы.
Решение.
Задача сводится к решению неравенства 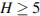 на интервале
на интервале 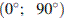 при заданных значениях начальной скорости
при заданных значениях начальной скорости 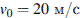 и ускорения свободного падения
и ускорения свободного падения 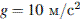 :
:
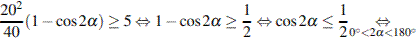
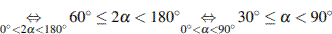 .
.
Ответ: 30.
Ответ: 30
Решение.
в правильной пирамиде вершина проецируется в центр основания, следовательно 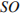 является высотой пирамиды. тогда по теореме Пифагора
является высотой пирамиды. тогда по теореме Пифагора
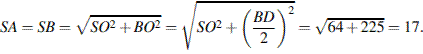
Ответ: 17.
Ответ: 17
ПЕРЕВОДНОЙ ЭКЗАМЕН ПО МАТЕМАТИКЕ 10 класс
ВАРИАНТ 3
ЧАСТЬ 1
1. Решите уравнение 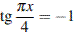 . В ответе напишите наибольший отрицательный корень.
. В ответе напишите наибольший отрицательный корень.
2. Материальная точка движется прямолинейно по закону 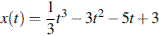 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
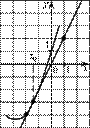
3. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
 Решение.
Решение.
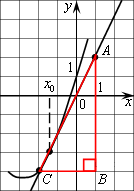 Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен углу ACB:
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен углу ACB:
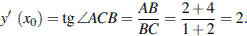
Ответ: 2.
Ответ: 2
4. На рисунке изображен график производной функции  . Найдите абсциссу точки, в которой касательная к графику
. Найдите абсциссу точки, в которой касательная к графику 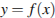 параллельна оси абсцисс или совпадает с ней.
параллельна оси абсцисс или совпадает с ней. 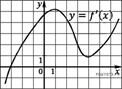
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, она имеет вид 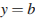 , и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка
, и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка 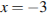 .
.
Ответ: -3.
Ответ: -3
5. В прямоугольном параллелепипеде 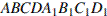 известно, что
известно, что 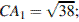
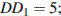
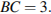 Найдите длину ребра
Найдите длину ребра 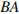 .
.
6. 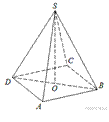 В правильной четырехугольной пирамиде
В правильной четырехугольной пирамиде 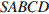 точка
точка 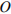 — центр основания,
— центр основания, 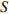 — вершина,
— вершина, 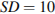 ,
, 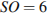 . Найдите длину отрезка
. Найдите длину отрезка 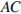 .
.
Решение.
В правильной пирамиде вершина проецируется в центр основания, следовательно, SO является высотой пирамиды. Тогда по теореме Пифагора
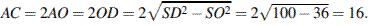
Ответ: 16.
Ответ: 16
7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

8. Найдите 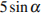 , если
, если 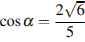 и
и 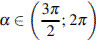 .
.
9. Найдите значение выражения 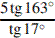 .
.
10. Небольшой мячик бросают под острым углом 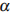 к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле
к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле 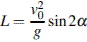 (м), где
(м), где 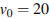 м/с – начальная скорость мячика, а
м/с – начальная скорость мячика, а 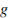 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте 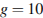 м/с
м/с 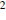 ). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?
). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?
11. Найдите наименьшее значение функции 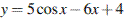 на отрезке
на отрезке 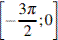 .
.
12. Найдите точку максимума функции 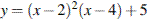
ЧАСТЬ 2
С1 а) Решите уравнение 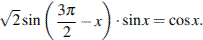
б) Найдите все корни этого уравнения, принадлежащие промежутку 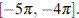
С2 В прямоугольном параллелепипеде 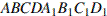 известны ребра:
известны ребра: 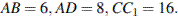 Найдите угол между плоскостями
Найдите угол между плоскостями 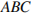 и
и 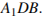
Дата: 2019-05-29, просмотров: 408.