Графические методы расчета позволяют проводить анализ нелинейных цепей переменного тока для частных значений параметров с использованием характеристик нелинейных элементов для мгновенных значений, по первым гармоникам и действующим значениям (см. табл. 1).

Графический метод с использованием характеристик для мгновенных значений

В общем случае методика анализа нелинейной цепи данным методом включает в себя следующие этапы:

-исходя из физических соображений находят (если он не задан) закон изменения одной из величин, определяющих характеристику 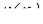нелинейного элемента;

-по нелинейной характеристике 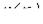для известного закона изменения переменной 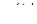путем графических построений определяют кривую 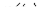(или наоборот);

-с использованием полученной зависимости 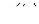проводят анализ остальной (линейной) части цепи.

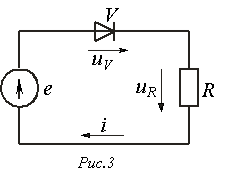
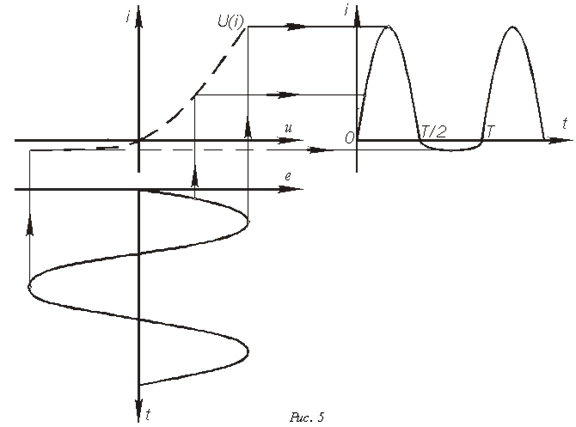
В качестве примера построим при синусоидальной ЭДС 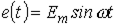кривую тока в цепи на рис. 3, ВАХ диода в которой представлена на рис. 4.

	Рис.4

Решение

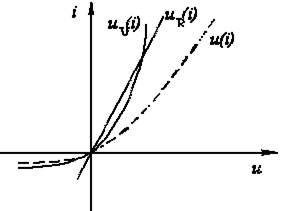
1. Строим результирующую ВАХ 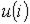цепи (см. рис. 4) согласно соотношению

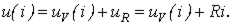
2. Находя для различных значений с использованием полученной кривой соответствующие им значения тока, строим по точкам (см. рис. 5) кривую искомой зависимости .

К полученному результату необходимо сделать следующий комментарий. Использование при анализе подобных цепей ВАХ идеального вентиля (обратный ток отсутствует, в проводящем направлении падение напряжения на диоде равно нулю) корректно при достаточно больших значениях амплитуд приложенного к диоду напряжения, определяющих значительное превышение током, протекающим через вентиль в прямом направлении, его обратного тока, вследствие чего последним можно пренебречь. При снижении величин напряжения, когда эти токи становятся сопоставимыми по величине, следует использовать ВАХ реального диода,представленную на рис. 4 и учитывающую наличие обратного тока.

Важнейшим элементом в цепях переменного тока является катушка с ферромагнитным сердечником. В общем случае кривая зависимости имеет вид гистерезисной петли, но, поскольку в устройствах, работающих при переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную (или начальную) кривую намагничивания.

Условное изображение нелинейной катушки индуктивности приведено на рис. 6. Здесь 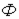– основной поток, замыкающийся по сердечнику, - поток рассеяния, которому в первом приближении можно поставить в соответствие потокосцепление рассеяния , где индуктивность рассеяния в силу прохождения потоком части пути по воздуху.

Для схемы на рис. 6 справедливо уравнение

,

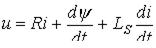(1)

где .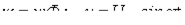

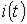В общем случае в силу нелинейности зависимости определить на основании (1) несинусоидальные зависимости и 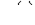достаточно непросто. Вместе с тем для реальных катушек индуктивности падением напряжения 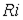и ЭДС, обусловленной потоками рассеивания, вследствие их малости, часто можно пренебречь. При этом из (1) получаем 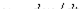, откуда

,

где постоянная интегрирования.

Так как характеристика катушки (см. рис. 7) симметрична относительно начала координат, а напряжение 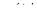симметрично относительно оси абсцисс (оси времени), то кривая 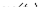также должна быть симметричной относительно последней, откуда следует, что .

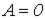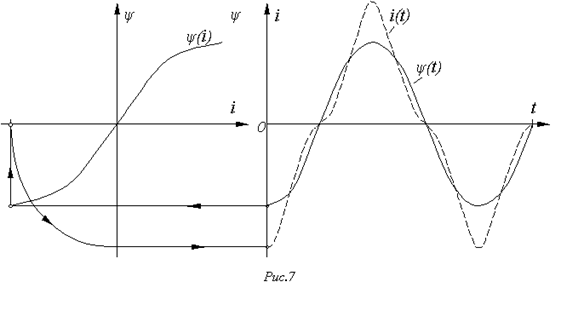
Находя для различных значений 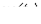с использованием кривой 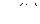соответствующие им значения тока, строим по точкам (см. рис. 7) кривую зависимости .

Анализ полученного результата позволяет сделать важный вывод: при синусоидальной форме потока напряжение 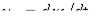на катушке синусоидально, а протекающий через нее ток имеет явно выраженную несинусоидальную форму. Аналогично можно показать, что при синусоидальном токе поток, сцепленный с катушкой, и напряжение на ней несинусоидальны.

Для среднего значения напряжения, наведенного потоком, можно записать

.

(2)

Умножив (2) на коэффициент формы, получим выражение для действующего значения напряжения

.

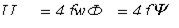
В частности, если напряжение и поток синусоидальны, то

.

Соотношение (2) является весьма важным: измеряя среднее значение напряжения, наведенного потоком, по (2) можно определить амплитуды потока 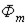и индукции 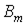при любой форме нелинейности катушки.

Аналогично проводится построение кривой при синусоидальном потоке и задании зависимости в виде петли гистерезиса. При этом следует помнить, что перемещение рабочей точки по петле осуществляется против часовой стрелки (см. рис. 8).

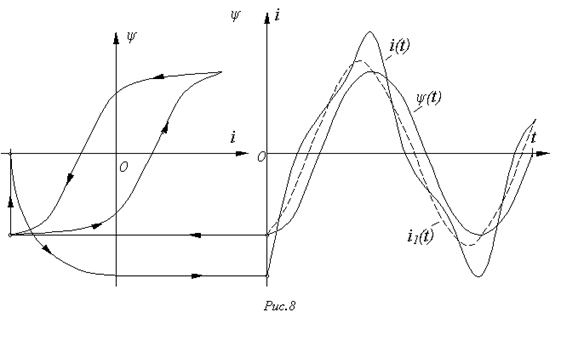К полученному результату следует сделать следующий важный комментарий. Разложение построенной кривой в ряд Фурье показывает, что первая гармоника тока (см. кривую на рис. 8) опережает по фазе потокосцепление и, следовательно, отстает по фазе от синусоидального напряжения на катушке на угол, меньший 90°. Это указывает ( ) на потребление катушкой активной мощности, затрачиваемой на перемагничивание сердечника и определяемой площадью петли гистерезиса.