Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Реализовать симметричный криптоалгоритм на основе простого гамиирования и с использованием сети Фейстеля. Для реализации последнего применить программу diskreet.

Провести статистический анализ открытых текстов и шифртекстов.

Пакет Norton Utilities содержит программу DISKREET, которая позволяет обеспечить защиту и шифровку файлов и создания виртуальных зашифрованных дисков. Для шифровки и защиты программы (файла) от несанкционированного доступа необходимо запустить программу DISKREET, указать в меню пункт Файл, указать путь шифруемого программного файла (с расширением com или exe), задать новое имя шифруемого файла, несколько отличающееся от старого, ввести пароль (не менее 6 символов), подтвердить его и запустить программу DISKREET, которая зашифрует файл и даст ему новое имя. Старый незашифрованный файл надо удалить. Для запуска зашифрованной программы надо расшифровать полученный новый файл при помощи программы DISKREET, запустив ее и введя пароль. С помощью программы DISKREET можно также зашифровать и текстовый файл (*. txt), который без расшифровки программой DISKREET нельзя будет прочитать при нажатии на клавишу F3. Зашифрованный текстовый файл должен иметь имя, отличающееся от исходного.

РАБОТА 3. АЛГОРИТМ AES

 

ПОСТАНОВКА ЗАДАЧИ

 

Разработать программное обеспечение, реализующее симметричный блочный алгоритм шифрования с переменной длинной блока и ключа Rijndael - улучшенный стандарт шифрования AES.

Использовать среду разработки Visual C++.

Составить описание алгоритма и описание особенностей непосредственной реализации алгоритма.

ОПИСАНИЕ АЛГОРИТМА

 

Rijndael - это симметричный блочный алгоритм шифрования с переменной длиной блока и ключа. Длины блока и ключа могут принимать значения 128, 192 и 256, причем в любой комбинации, варьируемое значение длины ключа составляет одно из достоинств стандарта AES, а вот "официальная" длина блока - только 128 бит.

Каждый блок открытого текста зашифровывается несколько раз в так называемых раундах (round) с помощью повторяющейся последовательности различных функций. Число раундов зависит от длины блока и ключа (см. таблицу 1).

 

Таблица 1 Число раундов в алгоритме Rijndael как функция от длины блока и ключа

Длина ключа в битах	Длина блока (в битах)
	128	192	256
128	10	12	14
192	12	12	14
256	14	14	14

 

Rijndael не относится к алгоритмам на сетях Фейстеля, которые характеризуются тем, что блок текста разбивается на левую и правую половины, затем преобразование раунда применяется к одной половине, результат складывается по модулю 2 с другой половиной, после чего эти половины меняются местами. Самым известным блочным алгоритмом из этой серии является DES. Rijndael, напротив, состоит из отдельных уровней, каждый из которых по-своему воздействует на блок в целом. Для зашифрования блока последовательно выполняются следующие преобразования:

Первый раундовый ключ складывается с блоком по модулю 2 (XOR).

Выполняются L_r - 1 обычных раундов.

 

Подстановка (S-блок)
ShiftRow
MixColumn
Сложение с раундовым ключом

Рис.1. Уровни преобразования внутри одного раунда алгоритма Rijndael

 

Выполняется завершающий раунд, в котором, в отличие от обычного, отсутствует преобразование MixColumn.

Каждый обычный раунд на этапе 2 состоит из четырех отдельных шагов.

Подстановка. Каждый байт блока заменяется значением, которое определяется S-блоком.

Перестановка. Байты в блоке переставляются с помощью преобразования ShiftRow.

Перемешивание. Выполняется преобразование MixColumn.

Сложение с раундовым ключом. Текущий раундовый ключ складывается с блоком по модулю 2.

Каждый уровень оказывает на каждый из блоков открытого текста определенное воздействие.

1. Влияние ключа

Сложение текста с ключом до первого раунда и на последнем шаге внутри каждого раунда влияет на каждый бит результата раунда. В процессе зашифрования результат каждого шага в каждом бите зависит от ключа.

2. Нелинейный уровень

Операция подстановки в S-блоке является нелинейной. Строение S-блоков обеспечивает почти идеальную защиту от дифференциального и линейного криптоанализа.

3. Линейный уровень

Преобразования ShiftRow и MixColumn обеспечивают максимальное перемешивание битов в блоке.

Далее в описании внутренних функций алгоритма Rijndael, через L_b будем обозначать длину блока в четырехбайтовых словах, через L_k - длину ключа пользователя в четырехбайтовых словах (то есть L_b, L_k Î {4, 6, 8}) и через L_r - число раундов (см. таблицу 1).

Открытый и зашифрованный тексты представлены в виде полей байтов и являются соответственно входом и выходом алгоритма.

Блок открытого текста, обрабатываемый как поле m₀,..., m_4Lb-1, представлен в виде двумерной структуры B (см. таблицу 2). в которой байты открытого текста отсортированы в следующем порядке:

 

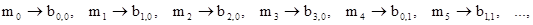
т.е. 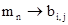, где i = n mod 4 и; j = ën/4û.

 

Таблица 2

b0,0	b0,1	b0,2	b0,3	b0,4	…	b0,Lb-1
b1,0	b1,1	b1,2	b1,3	b1,4	…	b1,Lb-1
b2,0	b2,1	b2,2	b2,3	b2,4	…	b2,Lb-1
b3,0	b3,1	b3,2	b3,3	b3,4	…	b3,Lb-1

 

Доступ к структуре B в функциях алгоритма Rijndael осуществляется по-разному, в зависимости от операции. S-блок оперирует с битами, ShiftRow - со строками (b_i,0, b_i,1, b_i,2, …, b_i,Lb-1) структуры B, а функции AddRoundKey и MixColumn - с четырехбайтовыми словами, обращаясь к столбцам .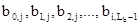

 

ВЫЧИСЛЕНИЕ КЛЮЧА РАУНДА

 

И для зашифрования, и для расшифрования требуется сгенерировать L_r раундовых ключей, совокупность которых называется разверткой ключа (key schedule). Развертка строится путем присоединения к секретному ключу пользователя, рекурсивно получаемых: четырехбайтовых слов

 

.

 

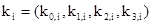Первые L_k слов  развертки ключа - это сам секретный ключ пользователя. Для L_k Î {4, 6} очередное четырехбайтовое слово k_i определяется как сумма по модулю 2 предыдущего слова k_i-1 со словом k_i-Lk. При i º 0 mod L_k перед операцией XOR нужно применить функцию F_Lk (k, i), которая включает в себя циклический сдвиг k байтов влево (операция r (k)), подстановку S (r (k)) с использованием S-блока алгоритма Rijndael (к этой операции мы еще вернемся) и сложение по модулю 2 с константой c (ëi/L_kû). Итоговое уравнение функции F таково:

 

F_Lk (k, i) = S (r (k)) Å c (ëi/L_kû).

 

Константы c (j) задаются равенством c (j) = (rc (j), 0, 0, 0), где значения rc (j) определяются рекурсивно как элементы поля F₂8:

 

rc (1) = 1, rc (j) = rc (j-1) х = х^j-1.

 

Или в виде численных значений:

 

rc (1) = '01’, rc (j) = rc (j-1) •'02'.

 

Программно значение rc (j) реализуется (j - 1) - кратным рекурсивным вызовом функции xtime, с начальным значением аргумента, равным 1 или более быстро - с использованием таблицы предвычислений (см. таблицу 3).

 

Таблица 3. Константы rc (j) (в шестнадцатеричном виде)

'01’	'02'	'04'	'08'	'10'	'20'	'40'	'80'	'1B'	'36'
'6C	'D8'	'AB'	'4D'	'9A'	'2F'	'5E'	'ВС	'63'	'C6'
'97'	'35'	'6A'	'D4'	'B3'	7O'	'FA'	'EF'	'C5	'91'

 

Для ключей длины 256 бит (то есть при L_k = 8) введена дополнительная операция подстановки: при i º 4 mod L_k перед операцией XOR значение k_i-1 заменяется на s (k_i-1).

Таким образом, развертка ключей состоит из L_b (L_r + 1) четырехбайтовых слов, включая и секретный ключ пользователя. На каждом раунде i = 0,..., L_r - 1 очередные L_b, четырехбайтовых слова с k_Lbi по k_{Lb (I+1)} выбираются из развертки и используются в качестве ключа раунда. Раундовые ключи рассматриваются, по аналогии с блоками открытого текста, как двумерная структура (см. таблицу 4).

 

Таблица 4. Представление раундовых ключей

k0,0	k 0,1	k 0,2	k 0,3	k 0,4	…	k 0,Lb-1
k 1,0	k 1,1	k 1,2	k 1,3	k 1,4	…	k 1,Lb-1
k 2,0	k 2,1	k 2,2	k 2,3	k 2,4	…	k 2,Lb-1
k 3,0	k 3,1	k 3,2	k 3,3	k 3,4	…	k 3,Lb-1

 

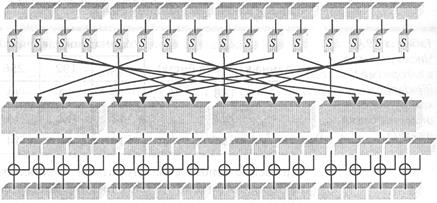
Для ключей длины 128 бит процесс генерации ключа изображен на рис.2.

 

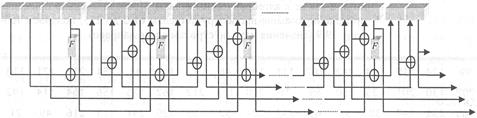
Рис.2. Диаграмма раундовых ключей для L_k = 4

 

Пока не известны слабые ключи, использование которых неблагоприятно сказалось бы на стойкости алгоритма Rijndael

S-БЛОК

 

Блок подстановки, или S-блок алгоритма Rijndael показывает, каким значением следует заменять каждый байт блока текста на каждом раунде. S-блок представляет собой список из 256 байтов. Сначала каждый ненулевой байт рассматривается как элемент поля F₂8 и заменяется мультипликативно обратным (нулевые байты остаются неизменными). Затем выполняется следующее аффинное преобразование над полем F₂ путем умножения на матрицу и сложения с вектором (11000110):

 

 

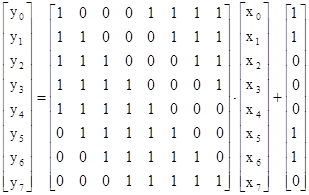
Здесь через х₀ и у₀ обозначены младшие, а через х₇ и у₇ - старшие биты в байте; вектор (11000110) длины 8 соответствует шестнадцатеричному числу '63'.

S-блок построен так, чтобы свести к минимуму чувствительность алгоритма к дифференциальному и линейному методам криптоанализа, а также к алгебраическим атакам. Последовательно применяя приведенную выше процедуру к числам от 0 до 255, получаем таблицу 5 (значения идут по строкам слева направо).

 

Таблица 5. Значения S-блока

99	124	119	123	242	107	111	197	48	1	103	43	254	215	171	118
202	130	201	125	250	89	71	240	173	212	162	175	156	164	114	192
183	253	147	38	54	63	247	204	52	165	229	241	113	216	49	21
4	199	35	195	24	150	5	154	7	18	128	226	235	39	178	117
9	131	44	26	27	110	90	160	82	59	214	179	41	227	47	132
83	209	0	237	32	252	177	91	106	203	190	57	74	76	88	207
208	239	170	251	67	77	51	133	69	249	2	127	80	60	159	168
81	163	64	143	146	157	56	245	188	182	218	33	16	255	243	210
205	12	19	236	95	151	68	23	196	167	126	61	100	93	25	115
96	129	79	220	34	42	144	136	70	238	184	20	222	94	11	219
224	50	58	10	73	6	36	92	194	211	172	98	145	149	228	121
231	200	55	109	141	213	78	169	108	86	244	234	101	122	174	8
186	120	37	46	28	166	180	198	232	221	116	31	75	189	139	138
112	62	181	102	72	3	246	14	97	53	87	185	134	193	29	158
225	248	152	17	105	217	142	148	155	30	135	233	206	85	40	223
140	161	137	13	191	230	66	104	65	153	45	15	176	84	187	22

 

При расшифровании порядок действий меняется на противоположный. Сначала выполняется обратное аффинное преобразование, затем мультипликативное обращение в поле F₂8. Обратный S-блок приведен в таблице 6.

 

Таблица 6. Значения обратного S-блока

82	9	106	213	48	54	165	56	191	64	163	158	129	243	215	251
124	227	57	130	155	47	255	135	52	142	67	68	196	222	233	203
84	123	148	50	166	194	35	61	238	76	149	11	66	250	195	78
8	46	161	102	40	217	36	178	118	91	162	73	109	139	209	37
114	248	246	100	134	104	152	22	212	164	92	204	93	101	182	146
108	112	72	80	253	237	185	218	94	21	70	87	167	141	157	132
144	216	171	0	140	188	211	10	247	228	88	5	184	179	69	6
208	44	30	143	202	63	15	2	193	175	189	3	1	19	138	107
58	145	17	65	79	103	220	234	151	242	207	206	240	180	230	115
150	172	116	34	231	173	53	133	226	249	55	232	28	117	223	110
71	241	26	113	29	41	197	137	111	183	98	14	170	24	190	27
252	86	62	75	198	210	121	32	154	219	192	254	120	205	90	244
31	221	168	51	136	7	199	49	177	18	16	89	39	128	236	95
96	81	127	169	25	181	74	13	45	229	122	159	147	201	156	239
160	224	59	77	174	42	245	176	200	235	187	60	131	83	153	97
23	43	4	126	186	119	214	38	225	105	20	99	85	33	12	125

ПРЕОБРАЗОВАНИЕ ShiftRow

 

Следующий шаг раунда - перестановка байтов в блоке. Порядок байтов меняется в строке (b_i,0, b_i,1, b_i,2,..., b_i,Lb-1) структуры В в соответствии с таблицами 7-9.

Операция ShiftRow для блоков длины 128 бит (L_b = 4)

 

До операции ShiftRow 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15

После операции ShiftRow 0 4 8 12 5 9 13 1 10 14 2 6 15 3 7 11

 

Операция ShiftRow для блоков длины 192 бит (L_b = 6)

 

До операции ShiftRow 0 4 8 12 16 20 1 5 9 13 17 21 2 6 10 14 18 22 3 7 11 15 19 23

После операции ShiftRow 0 4 8 12 16 20 5 9 13 17 21 1 10 14 18 22 2 6 15 19 23 3 7 11

 

Операция ShiftRow для блоков длины 256 бит (L_b = 8)

 

До операции ShiftRow 0 4 8 12 16 20 24 28 1 5 9 13 17 21 25 29 2 6 10 14 18 22 26 30 3 7 11 15 19 23 27 31

После операции ShiftRow 0 4 8 12 16 20 24 28 5 9 13 17 21 25 29 1 14 18 22 26 30 2 6 10 19 23 27 31 3 7 11 15

 

Все нулевые строки остаются без изменений. В строках i = 1,2,3 байты циклически сдвигаются влево на c_{Lb, i} позиций: с позиции с номером j на позицию с номером j - c_{Lb, i} mod L_b, где значение c_{Lb, i} определяется по таблице 10.

Таблица 10. Размер сдвига строк в операции ShiftRow

Lb	cLb,1	cLb,2	cLb,3
4	1	2	3
6	1	2	3
8	1	3	4

 

При обратном преобразовании позиция с номером j в строках i = 1,2,3 сдвигается на позицию с номером j + c_{Lb, i} mod L_b.

 

ПРЕОБРАЗОВАНИЕ MixColumn

 

После того как выполнена последняя построчная перестановка, на следующем шаге каждый столбец (b_i,j) блока текста, где i = 0,...,3, j = 0,...,L_b, представляется в виде полинома над полем F₂8 и умножается на фиксированный полином a (x) = а₃x³ + а₂x² + а₁x + a₀ с коэффициентами a₀ (x) =x, a₁ (x) = 1, a₂ (x) = 1, a₃ (x) = х + 1. Затем вычисляется остаток от деления полученного произведения на модуль М (х) = х⁴ + 1. Таким образом, каждый байт столбца взаимодействует со всеми остальными байтами столбца. При построковом преобразовании ShiftRow на каждом раунде байты взаимодействуют друг с другом в других комбинациях. То есть эти две операции дают сильное перемешивание.

Этот шаг можно свести к умножению на матрицу:

 

 

Умножение на '02' (соответственно на х) мы уже реализовали в виде функции xtime (см. таблицу 3). Умножение на '03' (соответственно на х + 1) тоже сделано по аналогии.

Для обращения преобразования MixColumn умножаем каждый столбец (b_i,j) блока текста на полином г (х) = r₃х³ + r₂х² + r₁х + r₀ с коэффициентами r₀ (х) =х³ + х² + х, r₁ (х) = х³ + 1, r₂ (х) = х³ + х² + 1, r₃ (х) = х³ + х + 1 и приводим результат по модулю М (х) = х⁴ + 1. Соответствующая матрица имеет вид:

 

 

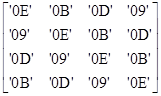
СЛОЖЕНИЕ С КЛЮЧОМ РАУНДА

 

На последнем шаге цикла раундовый ключ складывается по модулю 2 с блоком текста: