Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

МЕТОДЫ И СРЕДСТВА ЗАЩИТЫ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ

 

 

Екатеринбург 2005

Содержание

 

РАБОТА 1. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ТЕКСТОВ

РАБОТА 2. РЕАЛИЗАЦИЯ СИММЕТРИЧНОГО КРИПТОАЛГОРИТМА

РАБОТА 3. АЛГОРИТМ AES

1. ПОСТАНОВКА ЗАДАЧИ

2. ОПИСАНИЕ АЛГОРИТМА

2.1 ВЫЧИСЛЕНИЕ КЛЮЧА РАУНДА

2.2 S-БЛОК

2.3 ПРЕОБРАЗОВАНИЕ ShiftRow

2.4 ПРЕОБРАЗОВАНИЕ MixColumn

2.5 СЛОЖЕНИЕ С КЛЮЧОМ РАУНДА

2.6 ПОЛНАЯ ПРОЦЕДУРА ЗАШИФРОВАНИЯ БЛОКА

2.7 РАСШИФРОВАНИЕ

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

РАБОТА 4. КРИПТОСИСТЕМА PGP

1. ХАРАКТЕРИСТИКА PGP

2. КАК PGP РАБОТАЕТ

3. ОСНОВНЫЕ ШАГИ В ИСПОЛЬЗОВАНИИ PGP

4. ИНСТАЛЛЯЦИЯ PGP

5. ГЕНЕРАЦИЯ КЛЮЧЕЙ

6. КАК ПОСЛАТЬ ЗАШИФРОВАННОЕ СООБЩЕНИЕ

7. РАСШИФРОВКА СООБЩЕНИЙ

РАБОТА 5. ВИРУСЫ И АНТИВИРУСНЫЕ ПРОГРАММЫ

РАБОТА 6. ИССЛЕДОВАНИЕ СИСТЕМЫ БЕЗОПАСНОСТИ ОС

РАБОТА 7. ЗАЩИТА ОТ СЕТЕВЫХ АТАК

 

РАБОТА 2. РЕАЛИЗАЦИЯ СИММЕТРИЧНОГО КРИПТОАЛГОРИТМА

 

Реализовать симметричный криптоалгоритм на основе простого гамиирования и с использованием сети Фейстеля. Для реализации последнего применить программу diskreet.

Провести статистический анализ открытых текстов и шифртекстов.

Пакет Norton Utilities содержит программу DISKREET, которая позволяет обеспечить защиту и шифровку файлов и создания виртуальных зашифрованных дисков. Для шифровки и защиты программы (файла) от несанкционированного доступа необходимо запустить программу DISKREET, указать в меню пункт Файл, указать путь шифруемого программного файла (с расширением com или exe), задать новое имя шифруемого файла, несколько отличающееся от старого, ввести пароль (не менее 6 символов), подтвердить его и запустить программу DISKREET, которая зашифрует файл и даст ему новое имя. Старый незашифрованный файл надо удалить. Для запуска зашифрованной программы надо расшифровать полученный новый файл при помощи программы DISKREET, запустив ее и введя пароль. С помощью программы DISKREET можно также зашифровать и текстовый файл (*. txt), который без расшифровки программой DISKREET нельзя будет прочитать при нажатии на клавишу F3. Зашифрованный текстовый файл должен иметь имя, отличающееся от исходного.

РАБОТА 3. АЛГОРИТМ AES

 

ПОСТАНОВКА ЗАДАЧИ

 

Разработать программное обеспечение, реализующее симметричный блочный алгоритм шифрования с переменной длинной блока и ключа Rijndael - улучшенный стандарт шифрования AES.

Использовать среду разработки Visual C++.

Составить описание алгоритма и описание особенностей непосредственной реализации алгоритма.

ОПИСАНИЕ АЛГОРИТМА

 

Rijndael - это симметричный блочный алгоритм шифрования с переменной длиной блока и ключа. Длины блока и ключа могут принимать значения 128, 192 и 256, причем в любой комбинации, варьируемое значение длины ключа составляет одно из достоинств стандарта AES, а вот "официальная" длина блока - только 128 бит.

Каждый блок открытого текста зашифровывается несколько раз в так называемых раундах (round) с помощью повторяющейся последовательности различных функций. Число раундов зависит от длины блока и ключа (см. таблицу 1).

 

Таблица 1 Число раундов в алгоритме Rijndael как функция от длины блока и ключа

Длина ключа в битах	Длина блока (в битах)
	128	192	256
128	10	12	14
192	12	12	14
256	14	14	14

 

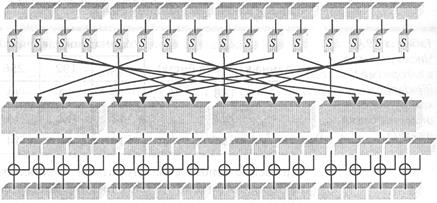
Rijndael не относится к алгоритмам на сетях Фейстеля, которые характеризуются тем, что блок текста разбивается на левую и правую половины, затем преобразование раунда применяется к одной половине, результат складывается по модулю 2 с другой половиной, после чего эти половины меняются местами. Самым известным блочным алгоритмом из этой серии является DES. Rijndael, напротив, состоит из отдельных уровней, каждый из которых по-своему воздействует на блок в целом. Для зашифрования блока последовательно выполняются следующие преобразования:

Первый раундовый ключ складывается с блоком по модулю 2 (XOR).

Выполняются L_r - 1 обычных раундов.

 

Подстановка (S-блок)
ShiftRow
MixColumn
Сложение с раундовым ключом

Рис.1. Уровни преобразования внутри одного раунда алгоритма Rijndael

 

Выполняется завершающий раунд, в котором, в отличие от обычного, отсутствует преобразование MixColumn.

Каждый обычный раунд на этапе 2 состоит из четырех отдельных шагов.

Подстановка. Каждый байт блока заменяется значением, которое определяется S-блоком.

Перестановка. Байты в блоке переставляются с помощью преобразования ShiftRow.

Перемешивание. Выполняется преобразование MixColumn.

Сложение с раундовым ключом. Текущий раундовый ключ складывается с блоком по модулю 2.

Каждый уровень оказывает на каждый из блоков открытого текста определенное воздействие.

1. Влияние ключа

Сложение текста с ключом до первого раунда и на последнем шаге внутри каждого раунда влияет на каждый бит результата раунда. В процессе зашифрования результат каждого шага в каждом бите зависит от ключа.

2. Нелинейный уровень

Операция подстановки в S-блоке является нелинейной. Строение S-блоков обеспечивает почти идеальную защиту от дифференциального и линейного криптоанализа.

3. Линейный уровень

Преобразования ShiftRow и MixColumn обеспечивают максимальное перемешивание битов в блоке.

Далее в описании внутренних функций алгоритма Rijndael, через L_b будем обозначать длину блока в четырехбайтовых словах, через L_k - длину ключа пользователя в четырехбайтовых словах (то есть L_b, L_k Î {4, 6, 8}) и через L_r - число раундов (см. таблицу 1).

Открытый и зашифрованный тексты представлены в виде полей байтов и являются соответственно входом и выходом алгоритма.

Блок открытого текста, обрабатываемый как поле m₀,..., m_4Lb-1, представлен в виде двумерной структуры B (см. таблицу 2). в которой байты открытого текста отсортированы в следующем порядке:

 

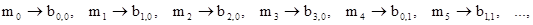
т.е. 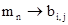, где i = n mod 4 и; j = ën/4û.

 

Таблица 2

b0,0	b0,1	b0,2	b0,3	b0,4	…	b0,Lb-1
b1,0	b1,1	b1,2	b1,3	b1,4	…	b1,Lb-1
b2,0	b2,1	b2,2	b2,3	b2,4	…	b2,Lb-1
b3,0	b3,1	b3,2	b3,3	b3,4	…	b3,Lb-1

 

Доступ к структуре B в функциях алгоритма Rijndael осуществляется по-разному, в зависимости от операции. S-блок оперирует с битами, ShiftRow - со строками (b_i,0, b_i,1, b_i,2, …, b_i,Lb-1) структуры B, а функции AddRoundKey и MixColumn - с четырехбайтовыми словами, обращаясь к столбцам .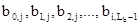

 

ВЫЧИСЛЕНИЕ КЛЮЧА РАУНДА

 

И для зашифрования, и для расшифрования требуется сгенерировать L_r раундовых ключей, совокупность которых называется разверткой ключа (key schedule). Развертка строится путем присоединения к секретному ключу пользователя, рекурсивно получаемых: четырехбайтовых слов

 

.

 

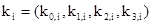Первые L_k слов  развертки ключа - это сам секретный ключ пользователя. Для L_k Î {4, 6} очередное четырехбайтовое слово k_i определяется как сумма по модулю 2 предыдущего слова k_i-1 со словом k_i-Lk. При i º 0 mod L_k перед операцией XOR нужно применить функцию F_Lk (k, i), которая включает в себя циклический сдвиг k байтов влево (операция r (k)), подстановку S (r (k)) с использованием S-блока алгоритма Rijndael (к этой операции мы еще вернемся) и сложение по модулю 2 с константой c (ëi/L_kû). Итоговое уравнение функции F таково:

 

F_Lk (k, i) = S (r (k)) Å c (ëi/L_kû).

 

Константы c (j) задаются равенством c (j) = (rc (j), 0, 0, 0), где значения rc (j) определяются рекурсивно как элементы поля F₂8:

 

rc (1) = 1, rc (j) = rc (j-1) х = х^j-1.

 

Или в виде численных значений:

 

rc (1) = '01’, rc (j) = rc (j-1) •'02'.

 

Программно значение rc (j) реализуется (j - 1) - кратным рекурсивным вызовом функции xtime, с начальным значением аргумента, равным 1 или более быстро - с использованием таблицы предвычислений (см. таблицу 3).

 

Таблица 3. Константы rc (j) (в шестнадцатеричном виде)

'01’	'02'	'04'	'08'	'10'	'20'	'40'	'80'	'1B'	'36'
'6C	'D8'	'AB'	'4D'	'9A'	'2F'	'5E'	'ВС	'63'	'C6'
'97'	'35'	'6A'	'D4'	'B3'	7O'	'FA'	'EF'	'C5	'91'

 

Для ключей длины 256 бит (то есть при L_k = 8) введена дополнительная операция подстановки: при i º 4 mod L_k перед операцией XOR значение k_i-1 заменяется на s (k_i-1).

Таким образом, развертка ключей состоит из L_b (L_r + 1) четырехбайтовых слов, включая и секретный ключ пользователя. На каждом раунде i = 0,..., L_r - 1 очередные L_b, четырехбайтовых слова с k_Lbi по k_{Lb (I+1)} выбираются из развертки и используются в качестве ключа раунда. Раундовые ключи рассматриваются, по аналогии с блоками открытого текста, как двумерная структура (см. таблицу 4).

 

Таблица 4. Представление раундовых ключей

k0,0	k 0,1	k 0,2	k 0,3	k 0,4	…	k 0,Lb-1
k 1,0	k 1,1	k 1,2	k 1,3	k 1,4	…	k 1,Lb-1
k 2,0	k 2,1	k 2,2	k 2,3	k 2,4	…	k 2,Lb-1
k 3,0	k 3,1	k 3,2	k 3,3	k 3,4	…	k 3,Lb-1

 

Для ключей длины 128 бит процесс генерации ключа изображен на рис.2.

 

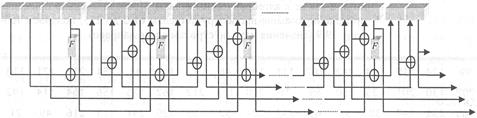
Рис.2. Диаграмма раундовых ключей для L_k = 4

 

Пока не известны слабые ключи, использование которых неблагоприятно сказалось бы на стойкости алгоритма Rijndael

S-БЛОК

 

Блок подстановки, или S-блок алгоритма Rijndael показывает, каким значением следует заменять каждый байт блока текста на каждом раунде. S-блок представляет собой список из 256 байтов. Сначала каждый ненулевой байт рассматривается как элемент поля F₂8 и заменяется мультипликативно обратным (нулевые байты остаются неизменными). Затем выполняется следующее аффинное преобразование над полем F₂ путем умножения на матрицу и сложения с вектором (11000110):

 

 

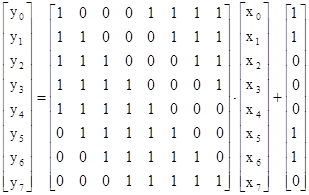
Здесь через х₀ и у₀ обозначены младшие, а через х₇ и у₇ - старшие биты в байте; вектор (11000110) длины 8 соответствует шестнадцатеричному числу '63'.

S-блок построен так, чтобы свести к минимуму чувствительность алгоритма к дифференциальному и линейному методам криптоанализа, а также к алгебраическим атакам. Последовательно применяя приведенную выше процедуру к числам от 0 до 255, получаем таблицу 5 (значения идут по строкам слева направо).

 

Таблица 5. Значения S-блока

99	124	119	123	242	107	111	197	48	1	103	43	254	215	171	118
202	130	201	125	250	89	71	240	173	212	162	175	156	164	114	192
183	253	147	38	54	63	247	204	52	165	229	241	113	216	49	21
4	199	35	195	24	150	5	154	7	18	128	226	235	39	178	117
9	131	44	26	27	110	90	160	82	59	214	179	41	227	47	132
83	209	0	237	32	252	177	91	106	203	190	57	74	76	88	207
208	239	170	251	67	77	51	133	69	249	2	127	80	60	159	168
81	163	64	143	146	157	56	245	188	182	218	33	16	255	243	210
205	12	19	236	95	151	68	23	196	167	126	61	100	93	25	115
96	129	79	220	34	42	144	136	70	238	184	20	222	94	11	219
224	50	58	10	73	6	36	92	194	211	172	98	145	149	228	121
231	200	55	109	141	213	78	169	108	86	244	234	101	122	174	8
186	120	37	46	28	166	180	198	232	221	116	31	75	189	139	138
112	62	181	102	72	3	246	14	97	53	87	185	134	193	29	158
225	248	152	17	105	217	142	148	155	30	135	233	206	85	40	223
140	161	137	13	191	230	66	104	65	153	45	15	176	84	187	22

 

При расшифровании порядок действий меняется на противоположный. Сначала выполняется обратное аффинное преобразование, затем мультипликативное обращение в поле F₂8. Обратный S-блок приведен в таблице 6.

 

Таблица 6. Значения обратного S-блока

82	9	106	213	48	54	165	56	191	64	163	158	129	243	215	251
124	227	57	130	155	47	255	135	52	142	67	68	196	222	233	203
84	123	148	50	166	194	35	61	238	76	149	11	66	250	195	78
8	46	161	102	40	217	36	178	118	91	162	73	109	139	209	37
114	248	246	100	134	104	152	22	212	164	92	204	93	101	182	146
108	112	72	80	253	237	185	218	94	21	70	87	167	141	157	132
144	216	171	0	140	188	211	10	247	228	88	5	184	179	69	6
208	44	30	143	202	63	15	2	193	175	189	3	1	19	138	107
58	145	17	65	79	103	220	234	151	242	207	206	240	180	230	115
150	172	116	34	231	173	53	133	226	249	55	232	28	117	223	110
71	241	26	113	29	41	197	137	111	183	98	14	170	24	190	27
252	86	62	75	198	210	121	32	154	219	192	254	120	205	90	244
31	221	168	51	136	7	199	49	177	18	16	89	39	128	236	95
96	81	127	169	25	181	74	13	45	229	122	159	147	201	156	239
160	224	59	77	174	42	245	176	200	235	187	60	131	83	153	97
23	43	4	126	186	119	214	38	225	105	20	99	85	33	12	125

ПРЕОБРАЗОВАНИЕ ShiftRow

 

Следующий шаг раунда - перестановка байтов в блоке. Порядок байтов меняется в строке (b_i,0, b_i,1, b_i,2,..., b_i,Lb-1) структуры В в соответствии с таблицами 7-9.

Операция ShiftRow для блоков длины 128 бит (L_b = 4)

 

До операции ShiftRow 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15

После операции ShiftRow 0 4 8 12 5 9 13 1 10 14 2 6 15 3 7 11

 

Операция ShiftRow для блоков длины 192 бит (L_b = 6)

 

До операции ShiftRow 0 4 8 12 16 20 1 5 9 13 17 21 2 6 10 14 18 22 3 7 11 15 19 23

После операции ShiftRow 0 4 8 12 16 20 5 9 13 17 21 1 10 14 18 22 2 6 15 19 23 3 7 11

 

Операция ShiftRow для блоков длины 256 бит (L_b = 8)

 

До операции ShiftRow 0 4 8 12 16 20 24 28 1 5 9 13 17 21 25 29 2 6 10 14 18 22 26 30 3 7 11 15 19 23 27 31

После операции ShiftRow 0 4 8 12 16 20 24 28 5 9 13 17 21 25 29 1 14 18 22 26 30 2 6 10 19 23 27 31 3 7 11 15

 

Все нулевые строки остаются без изменений. В строках i = 1,2,3 байты циклически сдвигаются влево на c_{Lb, i} позиций: с позиции с номером j на позицию с номером j - c_{Lb, i} mod L_b, где значение c_{Lb, i} определяется по таблице 10.

Таблица 10. Размер сдвига строк в операции ShiftRow

Lb	cLb,1	cLb,2	cLb,3
4	1	2	3
6	1	2	3
8	1	3	4

 

При обратном преобразовании позиция с номером j в строках i = 1,2,3 сдвигается на позицию с номером j + c_{Lb, i} mod L_b.

 

ПРЕОБРАЗОВАНИЕ MixColumn

 

После того как выполнена последняя построчная перестановка, на следующем шаге каждый столбец (b_i,j) блока текста, где i = 0,...,3, j = 0,...,L_b, представляется в виде полинома над полем F₂8 и умножается на фиксированный полином a (x) = а₃x³ + а₂x² + а₁x + a₀ с коэффициентами a₀ (x) =x, a₁ (x) = 1, a₂ (x) = 1, a₃ (x) = х + 1. Затем вычисляется остаток от деления полученного произведения на модуль М (х) = х⁴ + 1. Таким образом, каждый байт столбца взаимодействует со всеми остальными байтами столбца. При построковом преобразовании ShiftRow на каждом раунде байты взаимодействуют друг с другом в других комбинациях. То есть эти две операции дают сильное перемешивание.

Этот шаг можно свести к умножению на матрицу:

 

 

Умножение на '02' (соответственно на х) мы уже реализовали в виде функции xtime (см. таблицу 3). Умножение на '03' (соответственно на х + 1) тоже сделано по аналогии.

Для обращения преобразования MixColumn умножаем каждый столбец (b_i,j) блока текста на полином г (х) = r₃х³ + r₂х² + r₁х + r₀ с коэффициентами r₀ (х) =х³ + х² + х, r₁ (х) = х³ + 1, r₂ (х) = х³ + х² + 1, r₃ (х) = х³ + х + 1 и приводим результат по модулю М (х) = х⁴ + 1. Соответствующая матрица имеет вид:

 

 

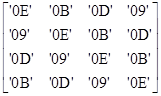
СЛОЖЕНИЕ С КЛЮЧОМ РАУНДА

 

На последнем шаге цикла раундовый ключ складывается по модулю 2 с блоком текста:

 

 

РАСШИФРОВАНИЕ

 

При расшифровании алгоритмом Rijndael процесс зашифрования выполняется в обратном порядке с обратными преобразованиями. Вот эти обратные функции:

InvFinalRound (word State, word RoundKey)

{

AddRoundKey (State, RoundKey);

InvShiftRow (State);

InvByteSub (State);

}

InvRound (word State, word RoundKey)

{

AddRoundKey (State, RoundKey);

InvMixColumn (State);

InvShiftRow (State);

InvByteSub (State);

}

Полная процедура расшифрования выглядит следующим образом:

InvRijndael (byte State, byte CipherKey)

{

KeyExpansion (CipherKey, ExpandedKey);

InvFinalRound (State, ExpandedKey + Nb*Nr);

for (i = Nr - 1; i > 0; i--)

InvRound (State, ExpandedKey + Nb*i);

AddRoundKey (State, ExpandedKey);

}

Алгебраическая структура алгоритма Rijndael позволяет упорядочить преобразования зашифрования так, что и для них можно будет использовать таблицы. Заметим, что подстановка S и преобразование ShiftRow коммутируют, поэтому внутри одного раунда их можно поменять местами. Благодаря свойству гомоморфизма 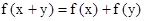 линейных преобразований, операции InvMixColumn и сложение с раундовым ключом можно тоже поменять местами. В пределах одного раунда это выглядит так:

InvFinalRound (word State, word RoundKey)

{

AddRoundKey (State, RoundKey);

InvByteSub (State);

InvShiftRow (State);

}

InvRound (word State, word RoundKey)

{

InvMixColumn (State);

AddRoundKey (State, InvMixColumn (RoundKey));

InvByteSub (State);

InvShiftRow (State);

}

Если порядок функций не менять, то их можно переопределить:

AddRoundKey (State, RoundKey);

InvRound (word State, word RoundKey)

{

InvByteSub (State);

InvShiftRow (State);

InvMixColumn (State);

AddRoundKey (State, InvMixColumn (RoundKey));

}

InvFinalRound (word State, word RoundKey)

{

InvByteSub (State);

InvShiftRow (State);

AddRoundKey (State, RoundKey);

}

Отсюда получаем структуру, аналогичную зашифрованию. Из соображений эффективности в процедуре lnvRound () отложим применение функции InvMixColumn к раундовому ключу до вычисления развертки, в которой первый и последний раундовые ключи из InvMixColumn оставим без изменений. "Обратные" раундовые ключи генерируются процедурой

InvKeyExpansion (byte CipherKey, word InvEpandedKey)

{

KeyExpansion (CipherKey, InvExpandedKey);

for (i = 1; i < Nr; i++)

InvMixColumn (InvExpandedKey + Nb*i);

}

Теперь полная процедура расшифрования выглядит так:

InvRijndael (byte State, byte CipherKey)

{

InvKeyExpansion (CipherKey, InvExpandedKey);

AddRoundKey (State, InvExpandedKey + Nb*Nr);

for (i = Nr-1; i>0; i--)

InvRound (State, InvExpandedKey + Nb*i);

InvFinalRound (State, InvExpandedKey);

}

По аналогии с зашифрованием можно и для расшифрования составить таблицы предвычислений. С помощью следующих преобразований:

 

 

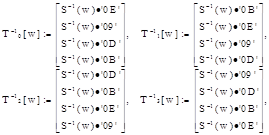
(где w = 0,...,255; S^-1 (w) - обратный S-блок подстановки) получаем результат обратного раундового преобразования блока 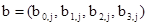 j = 0,..., L_b - 1:

 

,

 

где 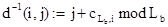 и 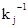 - j-й столбец "обратного" раундового ключа.

Здесь на последнем раунде тоже не выполняется преобразование MixColumn, и результатом последнего раунда будет

 

,

 

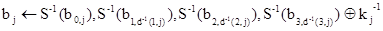где j = 0,…,L_b -1.

Для экономии памяти для расшифрования также можно составить таблицу всего из 256 четырехбайтовых слов, в которой

 

,

 

где r (а,b,c,d) = (d,a,b, с) - циклический сдвиг вправо на один байт.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. М. Вельшенбах. Криптография на Си и С++ в действии. М.: ТРИУМФ, 2004.

2. М. Яхтсмен. Теория и практика информационной безопасности. Под редакцией Зегжды П.Д. 1996.

3. Методы и средства защиты компьютерной информации. Методические указания к лабораторным работам для студентов специальности 220100 - Вычислительные машины, комплексы, системы и сети и направления 552800 - Информатика и вычислительная техника Сост.С. С. Соколов.

4. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005.33 с.

РАБОТА 4. КРИПТОСИСТЕМА PGP

 

Задание: провести шифрование и расшифрование текстов с помощью криптосистемы PGP.

ХАРАКТЕРИСТИКА PGP

 

PGP (Pretty Good Privacy) - это криптографическая (шифровальная) программа с высокой степенью надежности, которая позволяет пользователям обмениваться информацией в электронном виде в режиме полной конфиденциальности.

Главное преимущество этой программы состоит в том, что для обмена зашифрованными сообщениями пользователям нет необходимости передавать друг другу тайные ключи, т.к эта программа построена на новом принципе работы - публичной криптографии или обмене открытыми (публичными) ключами, где пользователи могут открыто посылать друг другу свои публичные ключи с помощью сети "Интернет" и при этом не беспокоиться о возможности несанкционированного доступа каких-либо третьих лиц к их конфиденциальным сообщениям.

В PGP применяется принцип использования двух взаимосвязанных ключей: открытого и закрытого. К закрытому ключу имеете доступ только вы, а свой открытый ключ вы распространяете среди своих корреспондентов.

Еще одно преимущество этой программы состоит также в том, что она бесплатная и любой пользователь, имеющий доступ к Интернету, может ее закачать на свой компьютер в течение получаса. PGP шифрует сообщение таким образом, что никто кроме получателя сообщения, не может ее расшифровать. Создатель PGP Филипп Циммерман открыто опубликовал код программы, который неоднократно был исследован специалистами крипто-аналитиками высочайшего класса и ни один из них не нашел в программе каких-либо слабых мест.

Филипп Циммерман следующим образом объясняет причину создания программы: "Людям необходима конфиденциальность. PGP распространяется как огонь в прериях, раздуваемый людьми, которые беспокоятся о своей конфиденциальности в этот информационный век. Сегодня организации по охране прав человека используют программу PGP для защиты своих людей за рубежом. Организация Amnesty International также использует ее". Пользователям сети Интернет рекомендуется использовать эту программу именно по той же причине, почему люди предпочитают посылать друг другу письма в конвертах, а не на открытках, которые могут быть легко прочитаны почтовыми служащими. Дело в том, что электронные сообщения, в том виде и формате, который существует на сегодняшний день, легко могут быть прочитаны и архивированы любым человеком, имеющим доступ к серверу Интернет провайдера (поставщика услуг сети Интернет). В настоящий момент спецслужбам проще и дешевле подключиться к электронным адресам большого количества лиц, нежели к телефонным разговорам. Здесь вообще ничего делать не надо. Все сделает компьютер. Агенту спецслужбы или другому заинтересованному человеку остается только сесть за компьютер и просмотреть все ваши сообщения. Научно-технический прогресс облегчил задачу таким людям, однако, этот же самый прогресс предоставил возможность пользователям сети Интернет скрыть свои сообщения от третьих лиц таким образом, что даже суперкомпьютер стоимостью несколько десятков миллионов долларов не способен их расшифровать.

 

КАК PGP РАБОТАЕТ

 

Когда пользователь шифрует сообщение с помощью PGP, то программа сначала сжимает текст, что сокращает время на отправку сообщения через модем и увеличивает надежность шифрования. Большинство приемов криптоанализа (взлома зашифрованных сообщений) основаны на исследовании рисунков, присущих текстовым файлам, что помогает взломать ключ. Сжатие ликвидирует эти рисунки и таким образом повышает надежность зашифрованного сообщения. Затем PGP генерирует сессионный ключ, который представляет собой случайное число, созданное за счет движений вашей мышки и нажатий на клавиши клавиатуры.

Как только данные будут зашифрованы, сессионный ключ зашифровывается с помощью публичного ключа получателя сообщения, который отправляется к получателю вместе с зашифрованным текстом.

Расшифровка происходит в обратной последовательности. Программа PGP получателя сообщения использует закрытый ключ получателя для извлечения временного сессионного ключа, с помощью которого программа затем дешифрует зашифрованный текст.

Ключи.

В то время как открытый и закрытый ключи взаимосвязаны, чрезвычайно сложно получить закрытый ключ исходя из наличия только открытого ключа, однако это возможно при наличии большой компьютерной мощности. Поэтому крайне важно выбирать ключи подходящего размера: достаточно большого для обеспечения безопасности и достаточно малого для обеспечения быстрого режима работы. Кроме этого, необходимо учитывать личность того, кто намеревается прочитать ваши зашифрованные сообщения, насколько он заинтересован в их расшифровке, каким временем он обладает, и какие у него имеются ресурсы.

Более большие ключи будут более надежными в течение более длительного срока времени. Поэтому если вам необходимо зашифровать информацию с тем, чтобы она хранилась в течение нескольких лет, то необходимо использовать более крупный ключ.

Ключи хранятся на жестком диске вашего компьютера в зашифрованном состоянии в виде двух файлов: одного для открытых ключей, а другого - для закрытых. Эти файлы называются "кольцами" (keyrings). В течение работы с программой PGP вы, как правило, будете вносить открытые ключи ваших корреспондентов в открытые "кольца". Ваши закрытые ключи хранятся в вашем закрытом "кольце". При потере вашего закрытого "кольца" вы не сможете расшифровать любую информацию, зашифрованную с помощью ключей, находящихся в этом "кольце".

Цифровая подпись.

Огромным преимуществом публичной криптографии также является возможность использования цифровой подписи, которая позволяют получателю сообщения удостовериться в личности отправителя сообщения, а также в целостности (верности) полученного сообщения. Цифровая подпись исполняет ту же самую функцию, что и ручная подпись. Однако ручную подпись легко подделать. Цифровую же подпись почти невозможно подделать.

Хэш-функция.

Еще одно важное преимущество использования PGP состоит в том, что PGP применяет так называемую "хэш-функцию", которая действует таким образом, что в том случае какого-либо изменения информации, пусть даже на один бит, результат "хэш-функции" будет совершенно иным. С помощью "хэш-функции" и закрытого ключа создается "подпись", передаваемая программой вместе с текстом. При получении сообщения получатель использует PGP для восстановления исходных данных и проверки подписи.

При условии использования надежной формулы "хэш-функции" невозможно вытащить подпись из одного документа и вложить в другой, либо каким-то образом изменить содержание сообщения. Любое изменение подписанного документа сразу же будет обнаружено при проверке подлинности подписи.

Парольная фраза.

Большинство людей, как правило, знакомы с парольной системой защиты компьютерных систем от третьих лиц. Парольная фраза - это сочетание нескольких слов, которое теоретически более надежно, чем парольное слово. В виду того, что парольная фраза состоит из нескольких слов, она практически неуязвима против так называемых "словарных атак", где атакующий пытается разгадать ваш пароль с помощью компьютерной программы, подключенной к словарю. Самые надежные парольные фразы должны быть достаточно длинными и сложными и должны содержать комбинацию букв из верхних и нижних регистров, цифровые обозначения и знаки пунктуации.

Парольная фраза должна быть такой, чтобы ее потом не забыть и чтобы третьи лица не могли ее разгадать. Если вы забудете свою парольную фразу, то уже никогда не сможете восстановить свою зашифрованную информацию. Ваш закрытый ключ абсолютно бесполезен без знания парольной фразы и с этим ничего не поделаешь.

 

ИНСТАЛЛЯЦИЯ PGP

 

Ниже приводятся заголовки сообщений, появляющиеся при инсталляции программы и команды, которые необходимо исполнять при инсталляции:

PGP Installation program:

Нажмите Next

Software License agreement:

Согласны ли вы с лицензионным соглашением? Если согласны, то тогда нажмите Yes

User information:

Информация о пользователе. Заполните необходимые поля и нажмите Next

Setup: choose installation directory:

Выберите каталог, куда будет проинсталлирована PGP. Если никаких особых пожеланий по этому поводу нет, то нажмите Next

Select components:

Программа инсталляции предлагает выбрать компоненты, которые будут установлены. Обязательны для инсталляции Program Files. Далее вы можете отметить птичкой плагин для той почтовой программы, которой вы пользуетесь. Если ее в списке нет, то ничего помечать не нужно. Можете также пометить файлы документации (User's manual) и программу PGP Disk for Windows (рекомендуется).

Нажмите Next.

Check setup information Пронрамма инсталляции что-то там проверит... Смело жмите Next и начнется копирование файлов на жесткий диск.

Для того чтобы программа автоматически запустила операцию создания ключей после перезагрузки компьютера нажать на кнопку "Yes I want to run PGP keys"

Нажмите Finish и на предложение программы инсталляции о перезапуске компьютеры ответьте положительно.

Компьютер перезапустится и на этом программа установки завершится.

Теперь необходимо сгенерировать два ключа:

public key - открытый ключ private key - закрытый ключ

ГЕНЕРАЦИЯ КЛЮЧЕЙ

 

После перезагрузки компьютера в правом нижнем углу панели задач (возле часов) появится значок PGP. Кликните по нему и выберите Launch PGP Keys

В меню Keys выберите пункт New Key. Нажмите Next и заполните необходимые формы (имя и E-Mail). Нажмите Next

Выберите размер ключа (2048 рекомендуется) и нажмите Next. Поставьте птичку напротив фразы "Key pair never expires" и нажмите Next.

Два раза введите парольную фразу и нажмите Next.

В процессе генерации ключей двигайте случайным образом мышью, можете нажать несколько клавиш на клавиатуре. Это необходимо программе для генерации ключей.

Когда программа выдаст сообщение о том, что процесс генерации закончен, нажмите Next и затем "Done".

На этом процесс создания пары ключей закончился и можно начинать пользоваться программой.

Теперь, после установки программы, необходимо обменяться со своими корреспондентами открытыми ключами. Для этого снова запустите PGP Keys, правой кнопкой мыши кликните файл со своим ключом и выберите пункт Export. Программа предложит вам выбрать путь и имя файла. Этот файл вы должны послать своему корреспонденту, в обмен на его открытый ключ. Когда вы получите необходимый ключт от своего корреспондента, двойным кликом мыши по нему начните процесс импорта (Import). Теперь можно пересылать друг другу зашифрованные сообщения, которые шифруются открытым ключом получателя сообщения.

 

РАСШИФРОВКА СООБЩЕНИЙ

Расшифровка вложений.

Сохраните вложение где-нибудь на жестком диске. Кликните по этому файлу правой кнопкой мыши и выберите пункт "PGP-Decrypt". Программа предложит ввести вашу парольную фразу и, если она была введена корректно, файл будет дешифрован.

 

МЕТОДЫ И СРЕДСТВА ЗАЩИТЫ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ

 

 

Екатеринбург 2005

Содержание

 

РАБОТА 1. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ТЕКСТОВ

РАБОТА 2. РЕАЛИЗАЦИЯ СИММЕТРИЧНОГО КРИПТОАЛГОРИТМА

РАБОТА 3. АЛГОРИТМ AES

1. ПОСТАНОВКА ЗАДАЧИ

2. ОПИСАНИЕ АЛГОРИТМА

2.1 ВЫЧИСЛЕНИЕ КЛЮЧА РАУНДА

2.2 S-БЛОК

2.3 ПРЕОБРАЗОВАНИЕ ShiftRow

2.4 ПРЕОБРАЗОВАНИЕ MixColumn

2.5 СЛОЖЕНИЕ С КЛЮЧОМ РАУНДА

2.6 ПОЛНАЯ ПРОЦЕДУРА ЗАШИФРОВАНИЯ БЛОКА

2.7 РАСШИФРОВАНИЕ

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

РАБОТА 4. КРИПТОСИСТЕМА PGP

1. ХАРАКТЕРИСТИКА PGP

2. КАК PGP РАБОТАЕТ

3. ОСНОВНЫЕ ШАГИ В ИСПОЛЬЗОВАНИИ PGP

4. ИНСТАЛЛЯЦИЯ PGP

5. ГЕНЕРАЦИЯ КЛЮЧЕЙ

6. КАК ПОСЛАТЬ ЗАШИФРОВАННОЕ СООБЩЕНИЕ

7. РАСШИФРОВКА СООБЩЕНИЙ

РАБОТА 5. ВИРУСЫ И АНТИВИРУСНЫЕ ПРОГРАММЫ

РАБОТА 6. ИССЛЕДОВАНИЕ СИСТЕМЫ БЕЗОПАСНОСТИ ОС

РАБОТА 7. ЗАЩИТА ОТ СЕТЕВЫХ АТАК