Модель процесу досягнення рівноваги, може бути використана для опису ситуації активних виробників, готових відразу ж відгукнутися на виникаючий попит. Подібний процес задається за допомогою наступної системи співвідношень: у торговий день t задана пропозиція  і воно визначає ціну
і воно визначає ціну 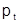 як вирішення рівняння
як вирішення рівняння
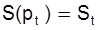 . (2.4)
. (2.4)
Ця ціна характеризує об'єм попиту
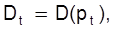 (2.5)
(2.5)
а пропозиція на наступний торговий день прямо орієнтується на попит попереднього дня
 (2.6)
(2.6)
Описаний процес також може бути представлений за допомогою павутиноподібної моделі, причому достатня умова збіжності має вигляд:
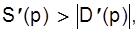 (2.7)
(2.7)
що відповідає сильнішій реакції виробників в порівнянні із споживачами. Проілюструємо обговорюваний процес досягнення рівноваги на приклад:
нехай функція пропозиції
S(p)= 4p - 3 (2.8)
а функція попиту
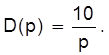 (2.9)
(2.9)
Основне співвідношення має вигляд
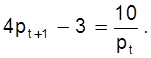 (2.10)
(2.10)
Звідси ціна в кожен наступний ринковий день визначається через ціну в попередній день по формулі:
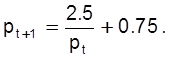 (2.11)
(2.11)
Припустимо, що початкова ціна  і зведемо результати розрахунку в таблицю 1.
і зведемо результати розрахунку в таблицю 1.
Таблиця 1. Збіжність ціни до рівноважної в часі
| P | D | S | E=D-S |
| 1,5 | 6,67 | 3 | 3,67 |
| 2,42 | 4,14 | 6,67 | -2,53 |
| 1,78 | 5,61 | 4,14 | 1,47 |
| 2,15 | 4,65 | 5,61 | -0,96 |
| 1,91 | 5,23 | 4,65 | 0,58 |
| 2,06 | 4,85 | 5,23 | -0,38 |
| 1,96 | 5,10 | 4,85 | 0,25 |
| 2,02 | 4,95 | 5,10 | -0,15 |
| 1,99 | 5,02 | 4,95 | 0,07 |
| 2,01 | 4,98 | 5,02 | -0,04 |
| 2,00 | 5 | 4,98 | 0,02 |
Таким чином, ми бачимо, що після 11 “ринкових” днів процес встановлення ціни сходиться до стану рівноваги, причому виходить вже відоме нам значення рівноважної ціни 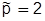 . Відмітимо, що проміжні значення ціни поперемінно стають то більше, то менше рівноважної величини. Це означає, що процес має коливальний характер з амплітудою, що зменшується (мал. 2.1) .[23, ст. 104].
. Відмітимо, що проміжні значення ціни поперемінно стають то більше, то менше рівноважної величини. Це означає, що процес має коливальний характер з амплітудою, що зменшується (мал. 2.1) .[23, ст. 104].
Строго монотонний характер має процес досягнення, відомий під назвою “нащупування”, в якому важливу роль грає зовнішнє (централізоване) регулювання. Ми розглянемо тут одну з моделей такого процесу, яка носить ім'я П.Самуельсона. У цій моделі зміна ціни прямо ставиться в залежність від величини надмірного попиту в торговий день t:
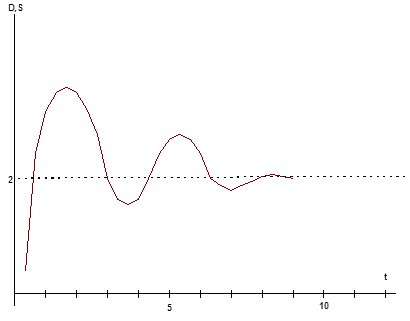
Мал. 2.3. Процес збіжності ціни до рівноважної
 (2.12)
(2.12)
При 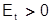 (попит більше пропозиції) ціна підвищується, інакше знижується. Цей процес сходиться при будь-якому співвідношенні між
(попит більше пропозиції) ціна підвищується, інакше знижується. Цей процес сходиться при будь-якому співвідношенні між  . Його найбільш поширена інтерпретація полягає в тому, що на ринку є арбітр (аукционер), який оцінює величину залишкового попиту і на підставі цієї оцінки оголошує ціну (
. Його найбільш поширена інтерпретація полягає в тому, що на ринку є арбітр (аукционер), який оцінює величину залишкового попиту і на підставі цієї оцінки оголошує ціну ( 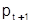 ) наступного дня, а всі учасники процесу неухильно слідують його вказівкам. Споживачі утворюють свій попит відповідно до функції попиту D(p), а виробники забезпечують випуск згідно функції пропозиції S(p). Величина а, яка називається параметром настройки, грає в цій схемі велику роль, оскільки при дуже малих його значеннях процес сходитися дуже поволі, а при дуже великих може і не сходиться до рівноваги.
) наступного дня, а всі учасники процесу неухильно слідують його вказівкам. Споживачі утворюють свій попит відповідно до функції попиту D(p), а виробники забезпечують випуск згідно функції пропозиції S(p). Величина а, яка називається параметром настройки, грає в цій схемі велику роль, оскільки при дуже малих його значеннях процес сходитися дуже поволі, а при дуже великих може і не сходиться до рівноваги.
Продемонструємо хід цього процесу на приведеному вище прикладі, причому покладемо значення параметра а = 0,1.
Основне співвідношення має вигляд
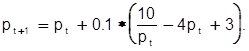 (2.13)
(2.13)
Результати розрахунків з 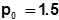 наведені в таблиці 2.
наведені в таблиці 2.
Таблиця 2. «Нащупування» рівноважної ціни по моделі П.Самуельсона
| p | D | S | E=D-S |
| 1,5 | 6,67 | 3 | 3,67 |
| 1,87 | 5,35 | 4,48 | 0,87 |
| 1,96 | 5,11 | 4,83 | 0,28 |
| 1,99 | 5,03 | 4,96 | 0,07 |
| 2 | 5 | 5 | 0 |
Дата: 2019-05-29, просмотров: 279.