Обезжиривание мелких деталей
Лужение
Растворение кислот, щелочей, солей:
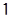
Кадмирование цианистое или серебрение
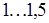
Свинцование
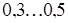
Травление
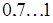
Хромирование
Цинкование цианистое
Пайка свинцом или третником
Лабораторные работы
При наличие в шкафу теплового источника (печи, горелки), объем удаляемого воздуха,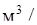 
ч, определяется по формуле:
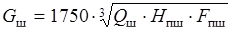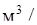, ч, (3.25)
где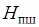 
- высота рабочих проемов шкафа, 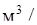ч; 
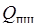- количество тепла, выделяемое внутри шкафа, Вт.
3.2.5.4 Отсасывающие панели
Отсасывающие панели применяются для удаления вредных выделений, увлекаемых конвективными потоками, в том числе, когда зона вредных выделений относительно велика и более полное укрытие организовать трудно. Отсасывающие панели следует применять при сварке, пайке, выдувке стекла, при удалении нагретых газов и пыли.
Расход воздуха через панель,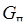 
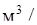, ч, вычисляется по формуле:
,, 
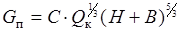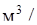ч, (3.26)
где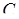 
- коэффициент, зависящий от конструкции панели и ее расположения относительно источников тепла; 
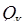– конвективная составляющая источника тепла, Вт.; 
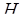- расстояние от верха плоскости до центра всасывающих отверстий панели, м.; 
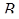- ширина источника тепла, м.
Коэффициент 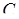принимается равным для панелей:
тип 1 (односторонняя панель)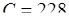 
тип 2 (панель с экраном)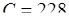
3.2.5.5. Бортовые отсосы
Бортовой отсос является основным местным отсосом от ванн в гальванических и травильных цехах и участках. В настоящее время распространение получили бортовые отсосы обычные и опрокинутые, каждый из которых может быть активирован поддувом воздуха (отсос с передувкой). Бортовые отсосы располагают с одной стороны ванны (однобортные отсосы) или с двух ее сторон (двубортные отсосы).
3.2.6. Разработка программной документации
На АРС “Охрана труда: компьютерное моделирование местной вентиляции” должен быть разработан документ “Руководства оператора” (Р. МИРЭА.00003-01 34 01).
Документ оформляется в соответствии с ГОСТ 19.505-79 и должен содержать следующие разделы:
назначение программы;
условия выполнения программы;
выполнение программы;
сообщения оператору.
Руководство должно содержать сведения, необходимые для обеспечения процесса интерактивного взаимодействия пользователя с АРС, и позволять облегчение процесса освоения разработанной АРС.
3.2.7. Результаты опытной эксплуатации системы и технические предложения по её развитию
В ходе опытной эксплуатации по методике представленной в Приложении 5 был сделан вывод, что система удовлетворяет требованиям заказчика.
В целом разработанная система вполне может быть использована как кафедрой “Охрана труда” в качестве дополнительного обучающего средства при выполнении студентами лабораторных работ, так и сотрудниками отделов ОТ на предприятиях.
АРС “Охрана труда” на следующих этапах разработки может быть расширена за счет дополнительных расчетных и информационных модулей, охватывающих другие направления ОТ производства, или за счет предоставления возможности выбора методик для существующих расчетов. Кроме того, АРС может быть дополнена развернутой диагностикой ошибок пользователя при вводе данных, а также модулем пояснения пользователю того, как был получен каждый конкретный результат, при желании с выдачей промежуточных результатов.
3.3. Автоматизированная обучающая система по курсу экономики
3.3.1. Постановка задачи и ее спецификация
Разрабатываемый модуль должен обеспечивать расчет одной из следующих неизвестных величин:
1) Приведенная стоимость;
2) Наращенная стоимость;
3) Длина интервала наращения;
4) Эффективная годовая ставка;
5) Интенсивность роста;
6) Коэффициента дисконтирования;
7) Коэффициента наращения.
Необходимо обеспечить удобство работы с программой пользователю, не являющемуся программистом. Модуль также должен удовлетворять требованиям, предъявленным при интегрировании его в состав целостного продукта.
Обучение пользователя желательно проводить на рабочих местах, что позволяет снизить затраты и повысить эффективность обучения и контроля. Наиболее удобным в этом случае является использование ПЭВМ, установленных на рабочих местах обучаемых. В настоящее время ПЭВМ все шире используется в самых различных областях человеческой деятельности. Это привело к тому, что большинство государственных предприятий и частных фирм имеют в своем распоряжении рабочие места с установленными на них ПЭВМ. За использование ПЭВМ также говорит и то, что малые ЭВМ серии СМ, которые также можно рассматривать в качестве технического средства для реализации, не удовлетворяют пользователя по скорости работы и отсутствию удобства в интерфейсе. С другой стороны, использование больших супер-ЭВМ, обладающих высокой скоростью обработки данных, также является нецелесообразным из-за дефицита машинного времени и вычислительных ресурсов, разделяемых между задачами большой важности и срочности.
Кроме того, следует принять во внимание психологический аспект использования персональных ЭВМ, находящихся в подразделениях, особенно человеком, по роду профессиональных занятий не связанному с вычислительной техникой, гораздо проще, чем посещение занятий на специализированном стенде, где техника отделена от пользователя и общение с ней происходит через операторов и системных программистов.
По мнению разработчиков, сказанное выше является достаточным основанием для выбора профессиональной ПЭВМ в качества аппаратных средств. Это позволяет реализовать диалоговый режим реального времени, работу с цветными панелями и меню, использование звуковых эффектов и тому подобное.
Также в соответствии с требованиями к системе, изложенными выше, были выбраны и программные средства для разработки системы. Было решено проводить разработку в системе MSM Workstation 2.0 Пользовательский диалог в стиле Windows знаком многим пользователям ПЭВМ, удобен в работе , требует распространенной среды MS Windows, не требует для своей работы мощных аппаратных средств.
Более подробно требования к аппаратным средствам сформулированы ниже:
- персональная ЭВМ, совместимая с IBM PC AT с тактовой частотой процессора не ниже 40 МГц;
- наличие цветного графического адаптера VGA;
- оперативная память не менее 16 МБайт;
- наличие операционной системы MS Windows 95 и выше.
- наличие жесткого диска и дисководов для 3.5” флоппи-дисков.
3.3.2. Обоснование проектных решений
3.3.2.1. Анализ при постоянной интенсивности наращения
Модель непрерывного начисления процентов
В банковской практике — особенно при электронных методах производства и регистрации финансовых операций - проценты могут начисляться за 1 сутки или даже за несколько часов. Например, коммерческий банк, находящийся в Москве, может одолжить определенную сумму денег банку, находящемуся во Владивостоке, на 12 часов — с 20 часов сегодняшнего дня до 8 часов следующего дня по московскому времени. За счет разницы во времени Владивостокский банк может добавить эти деньги к своему фонду краткосрочных ссуд, а затем вернуть долг с определенным процентом (или долями процента) к началу работы московского банка. Очевидно, что в этом и другом аналогичных случаях возникает задача начисления процентов за очень малые промежутки времени, т.е. по существу речь идет о непрерывном начислении процентов и их непрерывной капитализации.
При анализе инвестиций также возникает аналогичная задача, поскольку многие производственные и экономические процессы непрерывны по своей природе и такой же должна быть соответствующая им финансовая модель. В главах 1 и 2 мы построили несколько моделей начисления процентов при различной длине периода начисления (конверсионного периода) — от 1 дня до 1 года. Устремляя длину периода начисления к 0, построим теперь математическую модель непрерывного начисления процентов, рассмотрим способы практического применения непрерывной модели, а также сравним результаты дискретного и непрерывного начисления процентов. Для краткости иногда говорят "непрерывные проценты" , имея в виду непрерывное начисление и капитализацию процентов, т.е. бесконечно малый период начисления.
Постоянная интенсивность наращения
Примем за базовый период 1 год и обозначим целое число периодов начисления за год через т, а длину периода начисления через h = 1/т лет, m = 1,2,3,... . Тогда соответствующая положительная годовая ставка, и в силу формулы она связана с эффективной годовой ставкой.
Для простоты обозначим i — номинальная процентная ставка за один период начисления длиной h лет. Тогда из при h = m = 1 получаем
Для практики эффективную годовую ставку удобнее обозначать просто i.
Сделаем небольшое математическое пояснение. Для этого запишем коэффициент А(h) наращения эа любой период
(t, t + h) длиной h = 1/m на рассматриваемом интервале (О, T) в виде
Поскольку h мало, то различие между простыми и сложными процентами пренебрежимо мало. Так как A(0)=1, то— приращение 1 ден. ед. за малое время h (рис. 9.1, где h и т измеряются в годах).
Если А(т) дифференцируема в точке 0 справа, то
где g — угол наклона касательной к А(т) в точке т = 0.Из определения рассматриваемых ставок и результатов п. 2 § 8 следует, что если эффективная ставка i фиксирована, то номинальная ставка, при т —> и h = 1/т —> О монотонно убывает, оставаясь положительной. Поэтому существует положительное предельное значение, которое мы обозначим через: W.
ОПРЕДЕЛЕНИЕ. Предел 6 номинальной ставки W при т —> называется силой роста или интенсивностью наращения за год при непрерывном начислении процентов. Величину 8 можно назвать также номинальной годовой ставкой при непрерывном начислении процентов.
ТЕОРЕМА 3.1. Эффективная годовая ставка i и номинальная годовая ставка связаны соотношением
Доказательство. В курсе "Алгебра и начала анализа" доказывается, что
е = 2,718282 ... — замечательное число Эйлера (основание натуральных логарифмов). Поэтому в нашем случае
СЛЕДСТВИЕ.Справедлива и следующая двойственная к теореме 3.1
ТЕОРЕМА 9.2. Эффективная годовая ставка d дисконтирования и номинальная годовая ставка связаны соотношением
Для доказательства достаточно перейти к пределу в (3.7) при, использовав при этом вышеприведенные формулы.Формула (3.6) и соотношение и (3.2) позволяют составить таблицу 3.21, иллюстрирующую связь для нескольких значений i от 0,01 до 2) и при малых 1 до 0,10 достаточно близки. Однако с ростом 1" различие между тремя эквивалентными ставками быстро растет.
Таблица 3.21.
| D | G | I |
| 0,00990 | 0,00995 | 0,01 |
| 0,04761 | 0,04879 | 0,05 |
| 0,09091 | 0,09531 | 0,10 |
| 0,16667 | 0,18232 | 0,20 |
| 0,20000 | 0,22314 | 0,25 |
| 0,33333 | 0,40547 | 0,50 |
| 0,42857 | 0,55962 | 0,75 |
| 0,50000 | 0,69315 | 1,00 |
Пример 3.1. Найдем наращенное за 5 лет значение суммы S(0)=10 руб., если оно реинвестируется по постоянной ставке = 25% при следующих значениях m:
а) 1 раз в год,
б) 2 раза в год,в) непрерывно.г) Вычислим g для непрерывного начисления процентов.
Пример 3.2. Найдем коэффициент наращения A(т) за т = 1 год при реинвестировании по постоянной ставке = 1 ежегодно, ежеквартально, ежемесячно, ежечасно ежеминутно и непрерывно. Вычислим для каждого из случаев.
Таблица 3.22.
| Период начисления | m | A(1)=(1+1/m)m | iэф = A(1)-1 |
| Ежегодное Ежеквартальное Ежемесячное Ежедневное Ежечасное Ежеминутное Непрерывное | 1 4 12 360 8640 518400 | (1+1/1)1 =2 (1+1/4)4 =2,441406 (1+1/12)12 =2,613035 (1+1/360)360 =2,714516 (1+1/8640)8640 =2,718125 (1+1/518400)51840=2,718276 e=2,718282 | 1 1,441406 1,613035 1,714516 1,718125 1,718276 1,718282 |
Функциональная связь между любыми парами из основных параметров
В зависимости от условий задачи может оказаться удобным принять один из четырех основных параметров i, v и d за исходный и выразить через него значения трех остальных. В табл. 3.3 объединены ранее полученные соотношения.
Каждая строка этой таблицы показывает, как параметр, стоящий в обозначении этой строки, выражается через три остальные. Каждый столбец таблицы показывает, как через параметр, стоящий в обозначении этого столбца, выражаются три остальные.
Приближенная связь между основными параметрами
Из теории рядов известно, что при малых х с точностью до членов третьего порядка малости включительно
Подставляя первую из этих формул в (3.4), а вторую — в (3.6) и пренебрегая членами третьего порядка, получим, что при i или не более 0,10-0,20 можно пользоваться приближенными соотношениями: Аналогичным образом из формулы для суммы бесконечного числа членов сходящейся прогрессии следует, что при малых i
Этими приближенными формулами можно пользоваться для ориентировочных расчетов. Однако в финансовой практике надо пользоваться калькулятором или таблицами даже при малых i и
Коэффициенты наращения и дисконтирования при непрерывном наращении процентов
Предположим, что в настоящий момент tо производится инвестиция в сумме S(tо) по постоянной эффективной годовой ставке i. Тогда в силу формулы (3.5) для сложных процентов наращенная к моменту t = tо + т сумма АV1 составит
где время измеряется в годах, а i и g = ln(1+i) — десятичные дроби.
Если же нам предстоит в будущий момент t > tо уплатить или получить сумму S(t), то ее современная приведенная стоимость РV в настоящий момент tо составит
Итак, нами доказана следующая важная
ТЕОРЕМА 3.3. При постоянной эффективной годовой ставке i к номинальной годовой ставке ln(1 + i) коэффициент наращения зависит лишь от длины т интервала наращения, измеренной в годах, и составляет
Коэффициент дисконтирования за т лет равен
Заметим теперь, что А(т) — коэффициент наращения 1 ден. ед. на интервале (tо, tо + т} при движении по этому интервалу слева направо, т.е. в положительном направлении.
Равенство можно интерпретировать как отрицательное наращение, совпадающее с дисконтированием, поскольку движение по интервалу (t, t + т) происходит справа налево, т.е. в отрицательном направлении. Аналогичным образом интерпретируется равенство
Следовательно, в рассматриваемом случае коэффициенты наращения и дисконтирования взаимозаменяемы и с математической точки зрения можно было бы пользоваться только одним из них. Однако для наглядности удобнее пользоваться двумя коэффициентами в соответствии с прямым содержательным смыслом каждого из них.
Таким образом, как при дискретном, так и при непрерывном начислении сложных процентов справедливо фундаментальное соотношение
В частности, при т = 1 получаем из ранее установленных соотношений
Заметим теперь, что если функцию е задать на интервале то [-;+] при т > 0 она совпадает с А(т), а при т < 0 — с v(т):
При этом А'{0) — интенсивность наращения за базовую единицу времени.
Пример 3.3. Сумма 2000 долл. положена в банк под схему непрерывного начисления процентов с постоянной интенсивностью роста 10% за год. Найдем наращенную в конце года t сумму S(t) при t= 1, 2, 3, 5 и 10.
Решение. Здесь S(t) = 2000е, и ответ содержится в таблице 3.23.
Таблица 3.23.
| t, лет | 0 | 1 | 2 | 3 | 5 | 10 |
| S(t), $ | 2000 | 2210,34 | 2442,81 | 2699,72 | 3297,44 | 5436,56 |
Пример 3.5. Заемщик В должен уплатить кредитору А по векселю1000 долл. на 01.01.96, 2500 долл. на 01.01.97, 3000 долл. на 01.07.97.Найдем современную стоимость долга С(t) на моменты:а) 01.01.94 и б) 01.04.95 при = 0,06 за год.
3.3.2.2. Анализ при переменной интенсивности наращения
Описание модели и основная теорема
В настоящее время в мире действует много электронных бирж, связанных в единую мирону ю систему с несколькими центрами — в Нью-Иорке, Лондоне, Франкфурте и Токио. По существу, финансовые операции производятся круглые сутки, много раз за одну секунду. Поэтому даже за минуту на электронной бирже происходят колебания взаимных курсов основных валют, акций, облигаций и т.д. Эти колебания обычно небольшие, но наряду с интервалами относительной стабильности могут появляться и интервалы с устойчивой тенденцией к понижению (отрицательный тренд) или повышению (положительный трена) курса тех или иных денежных инструментов, а иногда происходят скачки курса. Возникает много сложных и интересных проблем, связанных с анализом и прогнозированием курса валют и связанных с ним курсов ценных бумаг. Все это оказывает влияние и на процентные ставки по обыкновенным вкладам и депозитам, которые также изменяются, хотя и не так часто, как валютный курс.
В качестве примера на рис. 10.1 приводится график среднемесячного дохода в процентах по вкладам в облагаемые налогами взаимные фонды денежного рынка США за 1975-1986 гг., заимствованный из [7]. Взаимные фонды денежного рынка (рис. 10.2) распределяют доходы от своих активов среди акционеров. Поэтому доходы акционеров увеличиваются или уменьшаются в зависимости от изменения годовых процентных ставок на краткосрочные ценные бумаги, в которые взаимные фонды вкладывают свои средства.
Период бурного роста активов взаимных фондов (от менее 10 млрд. долл. в 1974 г. до более 200 млрд. долл. в 1981 г., см. рис. 10.2) связан с резким подъемом до 12-16% ставок годового дохода в конце 70-х — начале 80-х годов.
Поэтому необходимо иметь аналитическую модель, в которой 6 и, следовательно, все другие процентные ставки зависят от времени. С этой целью рассмотрим коэффициент А(t, t + h) наращения на интервале (t, t + h) и примем
Здесь ih(t) — мгновенное значение в момент t годовой номинальной процентной ставки, которая зависит не только от длины Д интервала наращения, но и от момента t его начала. Поэтому коэффициент наращения А(t, t + h) также зависит теперь не только от hг, но и от t. Примем, что при всех t в рассматриваемом интервале существует предел
где (t) — мгновенное значение интенсивности роста за базовую единицу времени (обычно 1 год) в момент t. Из (3.12), (3.12) следует, что
Здесь означает производную по второму аргументу функции A(t, w) в точке w = t при произвольном, но фиксированном t.
Можно доказать, что справедлива следующая фундаментальная теорема.
ТЕОРЕМА 3.11. Примем, что (t) и А(tо,t) — непрерывные функция времени при и что в этом интервале выполняется принцип стабильности рынка. (4.7).
3.3.3 Разработка программной документации
Анализ непрерывного начисления процентов и непрерывного дисконтирования включает следующие блоки:
Расчет параметров непрерывного начисления процентов и непрерывного дисконтирования;
3.3.4. Результаты опытной эксплуатации игры и технические предложения по ее развитию
Модуль анализа непрерывного начисления процентов и непрерывного дисконтирования был разработан в полном объеме и отлажен по тестовым примерам расчетов.
Также по итогам опытной эксплуатации модуля разработчиками были сформулированы технические предложения по развитию системы, представленные ниже.
Программный комплекс должен в будущем создаваться совместными усилиями всех студентов, что объясняется схожими потребностями будь то предприятие, общественная организация, медицинское учреждение или учебное заведение, а также пожеланиями консультанта.
Структура программного комплекса должна определяться требованиями Заказчика, спецификой предметной области и задачами, которые должен решать этот программный комплекс, в том числе:
- представлять теоретические сведения;
- в интерактивном режиме запрашивать необходимые исходные данные, производить расчеты и немедленно выводить результаты, что позволит изменяя значения параметров, определять зависимости;
- создать "дружественную" среду работающему пользователю, оставляя возможность в любой момент прекратить сеанс диалога с программой, предлагая производить необходимые действия в удобной для того форме, блокируя неразрешенные манипуляции, сопровождая работу постоянной помощью в виде подсказок и меню.
Одни из выше перечисленных функций должны быть реализованы отдельными программными модулями, другие реализуются параллельно другими модулями.
С учетом вышесказанного структура предполагает наличие следующих компонент:
- модуль главного меню;
- модуль ввода параметров системы;
- модуль расчета непрерывного начисления процентов и непрерывного дисконтирования;
- модуль вывода расчетных значений;
- модуль работы с выходными данными в аналитическом виде;
Дата: 2019-04-23, просмотров: 197.
