Для принятия инвестиционного решения необходимо ответить на основные вопросы: какова величина ожидаемого дохода, каков предполагаемый риск, насколько адекватно ожидаемый доход компенсирует предполагаемый риск. Помочь решить эти проблемы позволяет современная теория портфеля, основателям которой являются Гарри Марковиц. Эта теория исходит из предположения, что инвестор располагает определенной суммой денег для осуществления инвестиций на определенный период времени, в конце которого он продает свои инвестиции и либо истратит деньги, либо реинвестирует их. И все это производится в условиях эффективного рынка.
Эффективно функционирующий рынок может выступить в трех формах: слабая форма: цены на акции полностью отражают всю информацию, заложенную в модели изменения цены за предшествующие периоды; полусильная форма: цены на акции отражают не только ту информацию, которая относится к прошлому периоду, но и другую соответствующую публикуемую информацию; сильная форма: доступна любая, поступающая на рынок информация, включая даже внутреннюю информацию компании.
Еще раз уточним, что под риском понимается вероятность недополучения дохода по инвестициям. Показатель "ожидаемая норма дохода" определяется по формуле средней арифметической взвешенной:
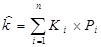 (9)
(9)
,где
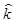 — ожидаемая норма дохода;
— ожидаемая норма дохода;
ki- норма дохода при i-том состоянии экономики;
Pi- вероятность наступления i-го состояния экономики;
n- номер вероятного результата.
При этом под доходом понимается что общий доход, полученный инвестором за весь период владения ценной бумагой (дивиденды, проценты плюс продажная цена), деленный на покупную цену ценной бумаги. Таким образом, для акции он равен:
( D1 + P1 )/Ро , (33) а для облигации (I1+P1)/Po ,где (10)
D1- ожидаемые дивиденды в конце периода,
I1 -ожидаемые процентные платежи в конце периода,
Ð1 - ожидаемая цена в конце периода (продажная цена),
Ро - текущая рыночная цена или покупная цена.
Например, если ожидается, что стоимость акции, продающейся в настоящий момент 50$ , к концу года повысится до 60$ , а ежегодные дивиденды в расчете на 1 акцию составят 2., 5% , то (D1+P1)/Po=(2,5+60)/50*100=125%
Для примера рассчитаем ожидаемую норму дохода по акциям 2-х компаний А и В
Таблица 4. Расчет ожидаемой нормы дохода
| Состояние экономики | Вероятность | Норма дохода по инвестициям по акциям | |
| A | B | ||
| Глубокий спад | 0,05 | -3,0 | -2,0 |
| Небольшой спад | 0,2 | 7,0 | 8,0 |
| Средний рост | 0,5 | 11,0 | 14,0 |
| Небольшой подъем | 0,20 | 14,0 | 16,0 |
| Мощный подъем | 0,05 | 21,0 | 26,0 |
| Ожидаемая норма дохода | 10,6 | 13,0 | |
Для измерения общего риска, используется ряд показателей из области математической статистики. Прежде всего, это показатель вариации, который измеряет нормы дохода. Для расчета вариации дискретного распределения (т. е. прорывного с конечным числом вариантов), используют формулу
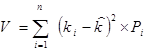 (11) ,
(11) ,
где V - вариация.
Таким образом, вариация - это сумма квадратных отклонений от средневзвешенной величины ожидаемой нормы дохода - взвешенных по вероятности каждого отклонения. Поскольку вариация измеряется в тех же единицах, что и доход(%), но возведенных в квадрат, очевидно, что оценить экономический смысл вариации для инвесторов затруднительно. Поэтому в качестве альтернативного показателя риска (отклонения от ожидаемой нормы дохода) обычно используют показатель "стандартная девиация" или среднее отклонение, являющееся квадратным корнем вариации:
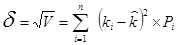 (12)
(12)
Стандартная девиация - это среднее квадратичное отклонение от ожидаемой нормы дохода. По акциям А стандартная девиация составит 5.2% . Тогда в случае нормального (симметричного) распределения дохода по данному проекту по теории вероятностей в 68 из 100 случаев (точнее, с вероятностью 68,26%)будущий доход окажется между 7,8% 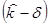 и 18,2%
и 18,2% 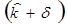 .
.
Вероятность того, что доход по данным акциям окажется в пределах между 2,6 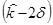 и 23,4%
и 23,4%  составит 95,46%
составит 95,46% 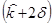 . В общем виде, пределы вероятностей для нормального распределения показаны на рисунке 4.
. В общем виде, пределы вероятностей для нормального распределения показаны на рисунке 4.
Одним из возможных методов выбора вариантов инвестирования с учетом фактора риска являются применение так называемых правил доминирования. Эти правила, основываются на предпосылке, что средний рациональный инвестор стремится избежать риска, т.е. соглашается на дополнительный риск только в том случае, если это обещает ему повышенный доход. Правила доминирования позволяют выбрать Финансовый инструмент, обеспечивающий наилучшее соотношение дохода и риска. Они состоят в следующем:
1. При одинаковом уровне ожидаемого инвестирования из всех возможных вариантов инвестирования предпочтение отдается инвестиции с наивысшим доходом.
Для примера рассмотрим показатели, характеризующие ожидаемый доход и риск по пяти инвестициям (Табл. 3).
Согласно 1-ому правилу акция В является предпочтительной по сравнению с акцией С; согласно 2-ому правилу - акция Е является доминантой по отношению к акции С, а акция А - по отношению к акции D.
Для сравнения инвестиций с разной доходностью необходимо определить относительную величину риска по каждой из них. В этих целях
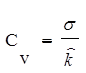 (13)
(13)
рассчитывают показатель "коэффициент вариации". Коэффициент вариации представляет собой риск на единицу ожидаемого дохода и рассчитывается как отношение стандартной девиации к ожидаемой номе дохода см. таблицу 5.
Рассчитав все показатели (ожидаемая норма дохода, вариация, коэффициент вариации) для двух видов акции, сведем в таблицу - . Данные таблицы 4 показывают, что определение рискованности финансового инструмента связано с тем, каким образом производится учет фактора риска. При оценке абсолютного риска, который характеризуется показателем стандартной девиации, акции В кажутся более рискованными чем акции А. Однако если учитывать относительный риск, т.е. риск на единицу ожидаемого дохода (через коэффициент вариации), то более рискованными окажутся все-таки акции А.
Выше нами рассматривалось измерение дохода и риска по отдельно взятой инвестиции. Ожидаемая норма дохода по портфелю инвестиций представляет собой средневзвешенную величину ожидаемых доходов по каждой отдельно и группе инвестиций, входящих в этот портфель:
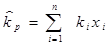
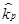 - ожидаемая норма дохода по портфелю инвестиций;
- ожидаемая норма дохода по портфелю инвестиций;
ki- ожидаемая норма дохода по i-той инвестиции;
хi- доля i -той инвестиции в портфеле;
n- номер инвестиции в портфеле.
| Показатели | Акции А | Акции В |
| Ожидаемая норма дохода | 10,60 | 13,00 |
| Вариация | 19,64 | 27,00 |
| Стандартная девиация | 4,43 | 5,2 |
| Коэффициент вариации | 0,42 | 0,40 |
Таблица 5. Оценка ожидаемого дохода и риска
Показатели вариации и стандартной девиации по портфелю рассчитываются так:
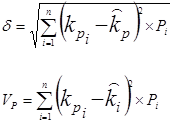 (15, 16)
(15, 16)
где- kpi доход по портфелю инвестиций при i-том состоянии экономики.
Для анализа портфеля инвестиций используется также такой показатель , как коэффициент корреляции. Корреляцией называется тенденция двух переменных менять свои значения взаимосвязанным образом. Эта тенденция измеряется коэффициентом корреляции r, который может варьироваться от +1,0 ( когда значения двух переменных изменяются абсолютно синхронно, (до -1.0) когда значения переменных движутся в точно противоположных направлениях). Нулевой коэффициент корреляции предполагает, что переменные никак не соотносятся друг с другом.
Цены двух абсолютно скоррелированных групп акций будут одновременно двигаться вверх и вниз. Это означает, что диверсификация не сократит риск, если портфель состоит из абсолютно положительно скоррелированных групп акций. В то же время риск может быть устранен полностью путем диверсификации при наличии абсолютной отрицательной корреляции.
Однако анализ реальной ситуации на биржах ведущих стран показывает, что, как правило, большинство различных групп акций имеет положительный коэффициент корреляции, хотя, конечно, не на уровне r = +1. Отсюда следует важный вывод о характере риска для портфеля, состоящего из различных групп акций: диверсификация сокращает риск , существующий по отдельным группам акций , но не может устранить его полностью. Для того, чтобы максимально использовать возможность диверсификации для сокращения риска по портфелю инвестиций, необходимо включать в него и другие Финансовые инструменты, например, облигации, золото. Таким образом, важнейший принцип диверсификации - распределение капитала между финансовыми инструментами, цены на которые по-разному реагируют на одни и те же экономическое события.
Более наглядно представить влияние величины портфеля на риск по портфелю инвестиций можно, обратившись к рисунку 5. График показывает, что риск по портфелю , состоящему из акций , представленных на Нью-йоркской фондовой бирже, имеет тенденцию к снижению с увеличением числа акций, входящих в портфель. Полученные данные свидетельствуют, что стандартная девиация по портфелю, состоящему из одной акции на этой бирже , составляет приблизительно 28%. Портфель, содержащий все зарегистрированные на бирже акции (в момент исследования их было 1500), называемый рыночным портфелем, имеет стандартную девиацию около 15,1%. Таким образом, включение в портфель большего количества акций позволяет сократить риск по портфелю практически в два раза.
Бета – коэффициенты. Как отмечалось, риск ценных бумаг можно разбить на два компонента: систематический риск, который нельзя исключить диверсификацией, и несистематический риск, который можно исключить: Риск ценной бумаги = Систематический риск +Несистематический риск. Любой инвестор, не питающий любви к риску будет исключать несистематический риск через диверсифицирование, поэтому относящийся к делу риск будет равен: Риск ценных бумаг = только систематический риск. Систематический риск можно измерить статистическим коэффициентом, называемым бета-коэффициентом. Бета-коэффициент измеряет относительную изменчивость ценной бумаги, рассчитываемую с помощью рыночного индекса ценных бумаг.
По определению бета для так называемой средней акции (акции, движение цены которой совпадает с общим для рынка, измеренной по какому-либо биржевому индексу), равна 1,0. Это значит, что, если, например, на рынке произойдет падение курсов акций в среднем на 10 процентных пунктов, таким же образом изменится и курс средней акции. Если, например, бета равна 0,5, то неустойчивость данной акции составляет лишь половину рыночной, т.е. ее курс будет расти и снижаться наполовину по сравнению с рыночным. Портфель из таких акций будет, следовательно, в 2 раза менее рискованным, чем портфель из акций с бета, равной 1,0. Интерпретация выборочных значений бета показана в таблице 7.
Бета для портфеля акций рассчитывается как средневзвешенная бета каждой отдельной акции:
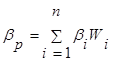 (17)
(17)
где bp-бета по портфелю акций;
bi- бета j- той акции;
wi доля i- той акции в портфеле;
h- номер акции в портфеле.
Но определять самостоятельно эту величину нет необходимости, т.к. специальные инвестиционно-консультационные компании регулярно рассчитывают и публикуют показатели бета для акций многих компаний. Кроме определения систематического риска, перед инвестором стоит еще одна задача - количественное измерение соотношения между уровнем риска и дохода.
Прежде всего, определим основные понятия, которые потребуются для решения данной задачи:  - ожидаемая норма дохода, по i—той акции;
- ожидаемая норма дохода, по i—той акции;
ki- необходимая норма дохода по i- той акции; (если  <k. то инвестор не будет покупать эту акцию или продаст ее, если является ее держателем). Если же
<k. то инвестор не будет покупать эту акцию или продаст ее, если является ее держателем). Если же  >ki ,то инвестор захочет купить эту акцию, (при
>ki ,то инвестор захочет купить эту акцию, (при  =ki -останется равнодушным);
=ki -останется равнодушным);
bi - коэффициент бета по i -той акции (бета по средней акции равна 1,0)
kh- необходимая норма дохода по рыночному портфелю ( или по средней акции)
Rph= (Kh-KRp) рыночная премия за риск дополнительный ( по сравнению с доходом по не рисковой ценной бумаге) доход, необходимый для компенсации среднего уровня риска '
Rpi= (Kh-KRp)*bp -риск по i-той акции ( она. будет меньше, равна или больше премии за риск по средней акции - рыночная премия за риск - в зависимости от того, будет ли bi меньше, равна или больше ba=1.0. Если bi=ba=1.0 то Rpi=Rpn)
Допустим, что в настоящее время доход по казначейским облигациям Kpi=9% необходимая норма дохода по средней акции Kh=15%. Тогда Rph=Kh-KRF=15-9=6%
Если bi=0,5 то Rpi=Rph*bi=6*0.5=3%
Если bi=1,5 то Rpi=Rph*bi=6*1.5=9%
Таким образом, чем больше bi-. тем больше должна быть и премия за риñк -Kpi и наоборот. Линия, являющаяся графическим изображением соотношения между систематическим риском, измеряется бета, и необходимой нормой дохода, называется Security Market Line (рис.5), а ее уравнение следующее:
Ki=KRF+(Kh+KRF)*bi=KRF+Rph+bI В нашем первом случае:
Ki=9+(15-9)*0,5=9+6+0,5=12%
Пусть другая акция -i- является более рискованной, чем акция j (bi=1,5) тогда
Ki=9*6*1,5=18%
Для средней акции с ba=1,0; Ka=9+6*1,0=15%=Kh
При этом надо учитывать, что премия по не рискованной ценной бумаге KRF слагается из 2-х элементов: реальной нормы дохода, т.е. нормы дохода без учета, инфляции -K*; и инфляционной премии - Ip , равной предполагаемому уровню инфляции.
Таким образом, KRF =K* +Ip
Реальная норма дохода по казначейским облигациям сложилась на уровне 2-4% (в среднем 3%). В связи с этим, показанная на графике KRP=9% включает в себя инфляционную премию 6%. Если ожидаемый уровень инфляции вырастет на 2%, то также соответственно на 2 % вырастет и необходимая норма дохода. KRF=K*+IP=3+6=9%.
Дата: 2019-05-29, просмотров: 309.