Расчетная площадь сечения с учетом только устойчивой части стенки:
.
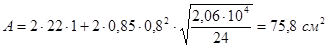| Параметр | Значение | ||
| A | Площадь поперечного сечения | 78.4 | см2 |
| a | Угол наклона главных осей инерции | -90.0 | град |
| Iy | Момент инерции относительно центральной оси Y1 параллельной оси Y | 1776.501 | см4 |
| Ix | Момент инерции относительно центральной оси X1 параллельной оси X | 26600.133 | см4 |
| It | Момент инерции при свободном кручении | 20.693 | см4 |
| iy | Радиус инерции относительно оси Y1 | 4.76 | см |
| ix | Радиус инерции относительно оси X1 | 18.42 | см |
| Wu+ | Максимальный момент сопротивления относительно оси U | 1182.228 | см3 |
| Wu- | Минимальный момент сопротивления относительно оси U | 1182.228 | см3 |
| Wv+ | Максимальный момент сопротивления относительно оси V | 161.5 | см3 |
| Wv- | Минимальный момент сопротивления относительно оси V | 161.5 | см3 |
| Wpl,u | Пластический момент сопротивления относительно оси U | 1337.8 | см3 |
| Wpl,v | Пластический момент сопротивления относительно оси V | 248.88 | см3 |
| Iu | Максимальный момент инерции | 26600.133 | см4 |
| Iv | Минимальный момент инерции | 1776.501 | см4 |
| iu | Максимальный радиус инерции | 18.42 | см |
| iv | Минимальный радиус инерции | 4.76 | см |
| au+ | Ядровое расстояние вдоль положительного направления оси Y(U) | 15.079 | см |
| au- | Ядровое расстояние вдоль отрицательного направления оси Y(U) | 15.079 | см |
| av+ | Ядровое расстояние вдоль положительного направления оси X(V) | 2.06 | см |
| av- | Ядровое расстояние вдоль отрицательного направления оси X(V) | 2.06 | см |
| yM | Координата центра тяжести по оси Y | 21.5 | см |
| xM | Координата центра тяжести по оси X | 0.4 | см |
Проверка устойчивости верхней части колонны в плоскости действия момента.
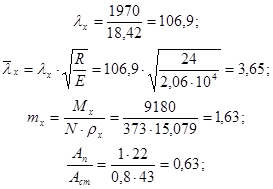
Значение коэффициента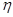 
определяем по прил. 10 [1] при 
:
;
;
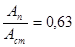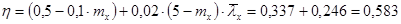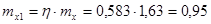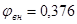по прил. 8 [1].
В расчетное сечение включаем всю площадь сечения:
.
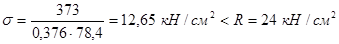Недонапряжение: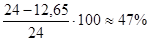 
.
Условие обеспечения общей устойчивости верхней части колонны в плоскости действия момента выполняется.
Проверка устойчивости стенки верхней части колонны:
,
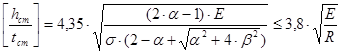где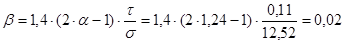 
.
;
;
;
.
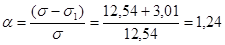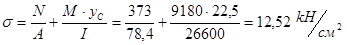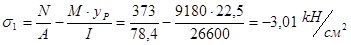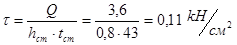Поскольку
,
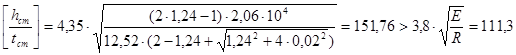принимаем
.
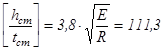Так как
,
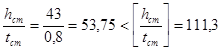условие соблюдается, следовательно проверку устойчивости колонны из плоскости действия момента проводят с учетом всей площади сечения.
Так как
,
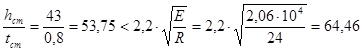Устойчивость стенки верхней части колонны обеспечена.
Проверка устойчивости верхней части колонны из плоскости действия момента
;
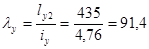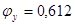по прил. 7 [1].
Для определения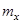 
найдем максимальный момент в средней трети расчетной длины стержня:
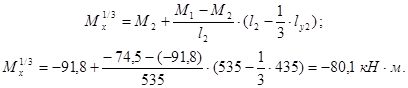
По модулю
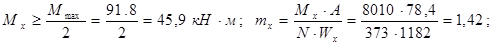
при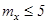 
коэффициент 
.
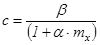Значения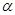 
и 
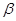определим по [ 1, прил. 11 ]:
.
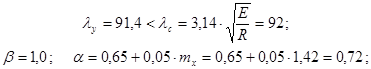
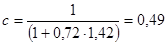Поскольку
,
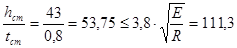в расчетное сечение включаем полное сечение стенки:
.
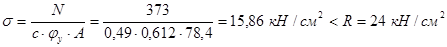Недонапряжение:
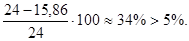
Условие обеспечения общей устойчивости верхней части колонны из плоскости действия момента выполняется.
Дата: 2019-05-29, просмотров: 234.
