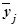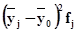Всероссийский заочный финансово-экономический институт
Кафедра Статистики
Курсовая работа
по дисциплине Статистика
на тему:
Статистические ряды распределения в изучении структуры рынка
Руководитель: Пуляшкин В.В.
Москва
2007
Введение
Статистические ряды распределения являются одним из наиболее важных элементов статистики. Они представляют собой составную часть метода статистических сводок и группировок, но, по сути, ни одно из статистических исследований невозможно произвести, не представив первоначально полученную в результате статистического наблюдения информацию в виде статистических рядов распределения. Первичные данные обрабатываются в целях получения обобщенных характеристик изучаемого явления по роду существенных признаков для дальнейшего осуществления анализа и прогнозирования; производится сводка и группировка; статистические данные оформляются с помощью рядов распределения в таблицы, в результате чего информация представляется в наглядном рационально изложенном виде, удобном для использования и дальнейшего исследования; строятся различного рода графики для наиболее наглядного восприятия и анализ информации. На основе статистических рядов распределения вычисляются основные величины статистических исследований: индексы, коэффициенты; абсолютные, относительные, средние величины и т.д., с помощью которых можно проводить прогнозирование, как конечный итог статистических исследований. Таким образом статистические ряды распределения являются базисным методом для любого статистического анализа. Понимание данного метода и навыки его использования необходимы для проведения статистических исследований.
В теоретической части курсовой работы рассмотрены следующие аспекты:
1) Понятие статистических рядов распределения, их виды;
2) Расчет средних величин, моды и медианы и представление рядов распределения графически;
Расчетная часть курсовой работы включает решение задачи по теме из варианта расчетного задания: Работа с таблицей «Выборочные данные торговых предприятий района: товарооборот и средние товарные запасы». Предметом исследования в работе будут служить так же торговые предприятия района (каждое предприятие, из которых, со своим товарооборотом). Работа содержит расчеты всех данных по ним, так же полное описание шагов действий для достижения конечного результата (вывода).
При написании курсовой работы использовались учебники курса, дополнительная литература, Интернет-ресурсы; при работе с табличными данными - персональный компьютер конфигурации:
Процессор – ADM Sempron 28000+S754
Память – DDR 512Mb PC3200 (DDR400) 
Жесткий диск – 120Gb 7200/8 Mb/SATA
Принтер – hp deskjet 3325, струйный
OC – Windows XP Professional
ППП – Microsoft Word 2002, Excel
Теоретическая часть
Расчетная часть
По результатам 20%-ного выборочного обследования торговых предприятий района, проведенного на основе случайной бесповторной выборки, получены следующие данные за отчетный месяц (тыс. руб.)
Таблица 1. Исходные данные
| № п\п | Товарооборот | Средние товарные запасы | № п\п | Товарооборот | Средние товарные запасы |
| 1 | 614 | 256 | 16 | 653 | 254 |
| 2 | 396 | 168 | 17 | 704 | 251 |
| 3 | 681 | 252 | 18 | 759 | 293 |
| 4 | 543 | 221 | 19 | 384 | 158 |
| 5 | 540 | 210 | 20 | 492 | 188 |
| 6 | 706 | 278 | 21 | 610 | 237 |
| 7 | 576 | 214 | 22 | 591 | 239 |
| 8 | 537 | 169 | 23 | 550 | 191 |
| 9 | 744 | 288 | 24 | 603 | 236 |
| 10 | 523 | 213 | 25 | 528 | 215 |
| 11 | 375 | 150 | 26 | 795 | 301 |
| 12 | 429 | 208 | 27 | 611 | 228 |
| 13 | 552 | 218 | 28 | 589 | 230 |
| 14 | 642 | 227 | 29 | 627 | 263 |
| 15 | 618 | 238 | 30 | 698 | 246 |
Цель статистического исследования - анализ совокупности предприятий по признакам Товарооборот и Средние товарные запасы, включая:
· изучение структуры совокупности по признаку Товарооборота;
· выявление наличия корреляционной связи между признаками Товарооборота и Средними товарными запасами предприятий, установление направления связи и оценка её тесноты;
· применение выборочного метода для определения статистических характеристик генеральной совокупности фирм.
Задание 1
По исходным данным (табл. 1) необходимо выполнить следующее:
1. Построить статистический ряд распределения предприятий по товарообороту, образовав пять групп с равными интервалами.
2. Графическим методом и путем расчетов определить значения моды и медианы полученного ряда распределения.
3. Рассчитать характеристики ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4. Вычислить среднюю арифметическую по исходным данным (табл. 1), сравнить её с аналогичным показателем, рассчитанным для интервального ряда распределения. Объяснить причину их расхождения.
Сделать выводы по результатам выполнения Задания 1.
Выполнение Задания 1
Целью выполнения данного Задания является изучение состава и структуры выборочной совокупности предприятий путем построения и анализа статистического ряда распределения фирм по признаку Товарооборот.
Задание 2
По исходным данным (табл. 1) с использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1. Установить наличие и характер корреляционной связи между признаками товарооборот и средние товарные запасы, образовав шесть групп с равными интервалами по каждому из признаков, используя методы:
а) аналитической группировки;
б) корреляционной таблицы.
2. Измерить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения задания 2.
Выполнение задания 2
Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, а также установление направления связи и оценка ее тесноты.
По условию Задания 2 факторным является признак товарооборот, результативным – признак средние товарные запасы.
1. Установление наличия и характера корреляционной связи между признаками товарооборотом и средними товарными запасами методами аналитической группировки и корреляционных таблиц
1а. Применение метода аналитической группировки
Аналитическая группировка строится по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение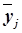 
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения 
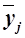систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х- товарооборот и результативным признаком Y – средние товарные запасы. Макет аналитической таблицы имеет следующий вид (табл. 7):
Таблица 7. Зависимость объема продаж от среднесписочной численности менеджеров
| Номер группы | Группы предприятий по товарообороту, тыс. руб. x | Число предприятий, fj | Средние товарные запасы, тыс. руб. | |
| всего | в среднем на одно предприятие,
| |||
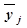
| 1 | 2 | 3 | 4 | 5=4:3 |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
|
| ИТОГО | |||
Групповые средние значения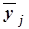 
получаем из таблицы 3, основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 8:
Таблица 8. Зависимость объема продаж от среднесписочной численности менеджеров
| Номер группы | Группы предприятий по товарообороту, тыс. руб. x | Число предприятий, fj | Средние товарные запасы, тыс. руб. | |
| всего | в среднем на одно предприятие,
| |||
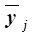
| 1 | 2 | 3 | 4 | 5=4:3 |
| 1 | 375-459 | 4 | 684 | 171 |
| 2 | 459-543 | 5 | 995 | 199 |
| 3 | 543-627 | 11 | 1508 | 228 |
| 4 | 627-711 | 7 | 1771 | 253 |
| 1 | 2 | 3 | 4 | 5 |
| 5 | 711-795 | 3 | 882 | 294 |
| ИТОГО | 30 | |||
6840
1145
Вывод. Анализ данных табл. 8 показывает, что с увеличением товарооборота от группы к группе систематически возрастает и средний товарный запас по каждой группе предприятий, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.
1б. Применение метода корреляционных таблиц
Корреляционная таблица строится как комбинация двух рядов распределения по факторному признаку Х и результативному признаку Y. На пересечении j-ой строки и k-ой графы таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый интервал по признаку Y. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками - прямой или обратной. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему, обратная - по диагонали от правого верхнего угла к левому нижнему.
Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Для факторного признака Х – Товарооборот эти величины известны из табл. 4 Определяем величину интервала для результативного признака Y – средние товарные запасы при k = 5, у max = 301 тыс. руб., у min = 150 тыс. руб.:
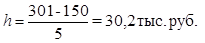
Границы интервалов ряда распределения результативного признака Y имеют вид:
Таблица 9
| Номер группы | Нижняя граница, Тыс. руб. | Верхняя граница, Тыс. руб. |
| 1 | 150 | 180,2 |
| 2 | 180,2 | 210,4 |
| 3 | 210,4 | 240,6 |
| 4 | 240,6 | 270,8 |
| 5 | 270,8 | 301 |
Подсчитывая для каждой группы число входящих в нее фирм с использованием принципа полуоткрытого интервала [ ), получаем интервальный ряд распределения результативного признака (табл. 10).
Таблица 10. Интервальный ряд распределения фирм по объёму продаж
| Группы предприятий по среднему товарному запасу, тыс. руб. у | Число предприятий, fj |
| 150-180,2 | 4 |
| 180,2-210,4 | 4 |
| 210,4-240,6 | 12 |
| 240,6-270,8 | 6 |
| 270,8-301 | 4 |
| ИТОГО | 30 |
Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 11).
Таблица 11. Корреляционная таблица зависимости объема продаж от среднесписочной численности менеджеров
| Группы предприятий по товарообороту, тыс. руб.
| Группы предприятий по среднему товарному запасу, тыс. руб.
| ИТОГО | ||||
| 150-180,2 | 180,2-210,4 | 210,4-240,6 | 240,6-270,8 | 270,8-301 | ||
| 375-459 | 2 | 1 | 3 | |||
| 459-543 | 1 | 2 | 2 | 5 | ||
| 543-627 | 1 | 1 | 9 | 1 | 12 | |
| 627-711 | 1 | 5 | 1 | 7 | ||
| 711-795 | 3 | 3 | ||||
| ИТОГО | 4 | 4 | 12 | 6 | 4 | 30 |
Вывод. Анализ данных табл. 11 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между среднесписочной численностью менеджеров и объемом продаж фирмами.
2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации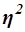 
и эмпирического корреляционного отношения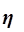 
Коэффициент детерминации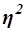 
характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии 
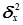признака Y в его общей дисперсии 
:
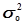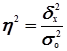
где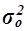 
– общая дисперсия признака Y,
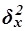– межгрупповая (факторная) дисперсия признака Y.
Общая дисперсия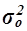 
характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных) и вычисляется по формуле
,
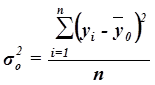где y i – индивидуальные значения результативного признака;
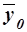– общая средняя значений результативного признака;
n – число единиц совокупности.
Межгрупповая дисперсия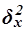 
измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
,
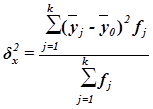где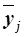 
–групповые средние,
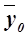– общая средняя,
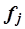–число единиц в j-ой группе,
k – число групп.
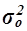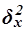Для расчета показателей и необходимо знать величину общей средней 
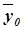, которая вычисляется как средняя арифметическая простая по всем единицам совокупности:
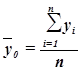
Значения числителя и знаменателя формулы имеются в табл. 8. Используя эти данные, получаем общую среднюю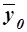 
:
= 
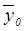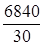=228 тыс. руб.
Для расчета общей дисперсии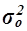 
применяется вспомогательная таблица 12.
Таблица 12. Вспомогательная таблица для расчета общей дисперсии
| Номер предприятия | Средние товарные запасы, тыс.руб. |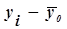 
| 
|
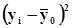
| 1 | 2 | 3 | 4 |
| 1 | 256 | 28 | 784 |
| 2 | 168 | -60 | 3600 |
| 3 | 252 | 24 | 576 |
| 4 | 221 | 7 | 49 |
| 5 | 210 | -18 | 324 |
| 6 | 278 | 50 | 2500 |
| 7 | 214 | -14 | 196 |
| 8 | 169 | -59 | 3481 |
| 9 | 288 | 60 | 3600 |
| 10 | 213 | -15 | 225 |
| 11 | 150 | -78 | 6084 |
| 12 | 208 | -20 | 400 |
| 13 | 218 | -10 | 100 |
| 14 | 227 | -1 | 1 |
| 15 | 238 | 10 | 100 |
| 16 | 254 | 26 | 676 |
| 17 | 251 | 23 | 529 |
| 18 | 293 | 65 | 4225 |
| 19 | 158 | -70 | 4900 |
| 20 | 188 | -40 | 1600 |
| 21 | 237 | 9 | 81 |
| 22 | 239 | 11 | 121 |
| 23 | 191 | -37 | 1369 |
| 24 | 236 | 2 | 64 |
| 25 | 215 | -13 | 169 |
| 26 | 301 | 73 | 5329 |
| 27 | 228 | 0 | 0 |
| 28 | 230 | 2 | 4 |
| 29 | 263 | 35 | 1225 |
| 30 | 246 | 18 | 324 |
| Итого | 6840 | 14 | 42636 |
Рассчитаем общую дисперсию:
= 
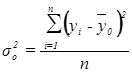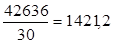
Для расчета межгрупповой дисперсии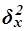 
строится вспомогательная таблица 13, При этом используются групповые средние значения 
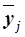из табл.
Таблица 13ю Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы предприятий по товарообороту, тыс. руб. x | Число предприятий, f j | Среднее значение в группе, тыс. руб. |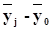 
|
|
| 1 | 2 | 3 | 4 | 5 |
| 375-459 | 4 | 171 | -57 | 12996 |
| 459-543 | 5 | 199 | -29 | 4205 |
| 543-627 | 11 | 228 | 0 | 0 |
| 627-711 | 7 | 253 | 25 | 4375 |
| 1 | 2 | 3 | 4 | 5 |
| 711-795 | 3 | 294 | 66 | 13068 |
| ИТОГО | 30 |
| 34644 |
Рассчитаем межгрупповую дисперсию:
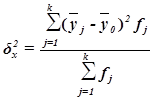
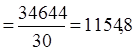
Определяем коэффициент детерминации:
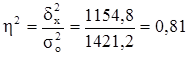или 81%
Вывод. 81% вариации объёма продаж товаров фирмами обусловлено вариацией среднесписочной численности менеджеров по продажам, а 19% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение 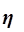оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
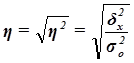
Рассчитаем показатель :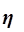
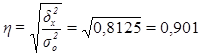= 90,1%
Вывод: согласно шкале Чэддока связь между товарооборотом и средними товарными запасами предприятий является весьма тесной.
Задание 3
По результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1) ошибку выборки для средней величины товарооборота торгового предприятия, а также границы, в которых будет находиться генеральная средняя.
2) ошибку выборки доли торговых предприятий с объемом товарооборота 627 и более тыс. руб., а также границы, в которых будет находиться генеральная доля фирм.
Выполнение Задания 3
Целью выполнения данного Задания является определение для генеральной совокупности предприятий района границ, в которых будут находиться средняя величина товарооборота, и доля предприятий с товарооборотом не менее 627 тыс. руб.
Задание 4
Имеются данные о продаже товара А на трех городских рынках:
Таблица 16
| Рынки | Базисный период | Отчетный период | ||
| Средняя цена за 1 кг., руб. (р0) | Продано, т (q0) | Изменение цены, % (p1) | Индекс физического объема(q1) | |
| 1 | 180 | 350 | 10 | 1,2 |
| 2 | 200 | 280 | Без изменений | 0,9 |
| 3 | 220 | 70 | -5 | 1,1 |
Определите:
1. Индексы цен переменного, постоянного состава и структурных сдвигов.
2. Абсолютное изменение средней цены товара в результате влияния отдельных факторов.
Таблица 17
|
Рынки
| Базисный период | Отчетный период | Расчетные графы | ||||
| Средняя цена за 1 кг., руб. (р0) | Продано, т (q0) | Изменение цены, % (p1) | Индекс физического объема (q1) | p0q0 | p1q1 | p0q1 | |
| 1 | 180 | 350 | 198 | 1,2 | 63000 | 70131,6 | 63756 |
| 2 | 200 | 280 | 200 | 0,9 | 56000 | 56504 | 56500 |
| 3 | 220 | 70 | 209 | 1,1 | 15400 | 14776,3 | 15554 |
| Итого | - | 700 | - | 134400 | 141407,9 | 135810 | |
Вычислим индекс цен переменного состава:
Ipпс=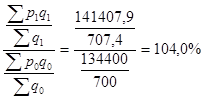 
Из таблицы видно, что цена продукции на каждом рынке в отчетном периоде по сравнению с базисным изменилась. В целом же средняя цена выросла на 4 % .Это объясняется влиянием изменений структуры реализации продукции по торговым городским рынкам. В базисном периоде по более низкой цене продавали продукцию меньше, чем в отчетном периоде по более высокой цене.
Рассчитываем индекс структурных сдвигов:
Ipccт=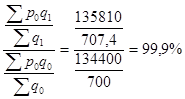 
Первая часть приведенной формулы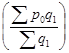 
позволяет ответить на вопрос, какой была бы средняя цена в отчетном периоде. Вторая часть формулы 
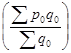отражает фактическую среднюю цену базисного периода.
Рассчитанный индекс показал, что за счет структурных сдвигов цены значительно не изменились.
Определим индекс фиксированного или постоянного состава, который не учитывает изменения структуры продаж:
Ipфс =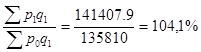 
Индекс цен фиксированного состава равен 104,1%, что позволяет сделать следующий вывод: если бы структура продаж продукции на городских рынках не изменилась, средняя цена возросла бы на 4,1%., что и произойдет в дальнейшем.
Между данными индексами существует следующая взаимосвязь:
Ipфс * Iccт = Ipпс ;
1,041 * 0,99 =1,040
Определим абсолютное изменение средней цены товара в результате влияния отдельных факторов:
D pq = åp1q1 - å p0q0
D pq = 141407,9 – 134400 =7008 руб.
Заключение
Статистические ряды распределения являются базисным методом для любого статистического анализа.
Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку, характеризует структуру изучаемого явления. Анализируя рассчитанные показатели статистического ряда распределения, можно делать выводы об однородности или неоднородности совокупности, закономерности распределения и границах варьирования единиц совокупности. Изучив основные приемы исследования и практики применения рядов распределения, а также методику вычисления наиболее важных статистических величин, необходимо отметить, что конечная цель изучения статистики в целом - анализ изучаемого явления - крайне важен для всех сфер человеческой жизни. Анализ отображает явления в целом и вместе с этим учитывает влияние каждого фактора в отдельности. На основании проведенного анализа можно учитывать и прогнозировать факторы, негативно влияющие на развитие событий.
Социально-экономическая статистика обеспечивает предоставление важной цифровой информации об уровне и возможностях развития страны: ее экономическом положении, уровне жизни населения, его составе и численности, рентабельности предприятий, динамике безработице и т.д. Статистическая информация является одним из решающих ориентиров государственной экономической политики.
Статистические методы используют комплексно. Выделяют три основные стадии экономико-статистического исследования: сбор первичной статистической информации, статистическая сводка и обработка первичной информации, обобщение и интепретация статистической информации.
Качество, достоверность статистической информации определяют эффективность использования статистики на любом уровне и в любой сфере.
Литература
1. Статистика: Учеб. пособие/А.В. Багат, М.М. Конкина, В.М. Симчера и др.; Под ред. В.М. Симчеры.- М.: Финансы и статистика, 2005.
2. Громыко Г.Л. Теория статистики: Учебник. - М.: ИНФРА-М, 2006.
3. Практикум по статистике: Учеб. пособие для вузов/ Под ред. В.М. Симчеры. - М.: Финстатинформ, 1999.
4. Гусаров В.М. Статистика: Учеб. пособие для вузов. - М.: ЮНИТИ - ДАНА, 2001.
5. Гусаров В.М. Статистика: Учеб пособие/ В.М. Гусаров, Е.И. Кузнецова. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007.
6. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под. ред. Башиной О.Э., Спирина А.А. – М.: Финансы и статисика, 2005.
7. Практикум по теории статистики: Учебное пособие/Под. ред. Шмойловой Р.А. – М.: Финансы и статистика, 2004.
8. Теория статистики: Учебник/Под. ред. Шмойловой Р.А. – М.: Финансы и статистика, 2001; 2003; 2006.
9. http://www.gks.ru
Всероссийский заочный финансово-экономический институт
Кафедра Статистики
Курсовая работа
по дисциплине Статистика
на тему:
Дата: 2019-05-29, просмотров: 204.
