В процесі розв’язку поставленої задачі оброблюються дані типу, що наводиться у таблиці 2.1.
Таблиця 1.1 – Типи даних, що будуть використовуватись при розробці програми
| Тип | Область значень | Фізичний формат |
| real | від 2,9×10-39 до 1,7×1038 | Точність 11-12 розрядів, розмір в байтах – 6 |
| integer | Від -32 768..32 767 (-2 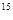 ..2 ..2 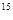 -1) -1)
| Розмір 2 байта |
1.6 Програмування на мові Pascal 7.0
Program pe4en;
uses crt;
Var M, L,b,z,z0,q,r,r1,ll,l2, d,d1,u,u1,Nm,Mmax,
sig1,
sig2,sig3,sig4,sigx,lamda :Real;
z :integer
{const Mmax=170;L=47.2;b=20;z=16;z0=10;q=2;r=35;r1=55;ll=23;l2=15;d=20;d1=50;
u=4.55;u1=3.115;Nm=0.9;{****Dla nalagodgenna****}
begin
clrscr;
writeln('vedit Mmax');
readln(Mmax);
writeln('dovginy tvirnoi');
readln(L);
writeln('vedit dovginy zybsa');
readln(b);
writeln('4iclo zybsiv satelita');
read(z);
writeln('4iclo zybsiv dicka');
readln(z0);
writeln('4iclo satelitov');
readln(q);
writeln('r --vidstan vid seredini ploshtini do ceredini zyba');
readln(r);
writeln('r1--vidstan do opornoi poverxni');
readln(r1);
writeln('dovgina posado4noi poverxni');
readln(ll);
writeln('dovgina oci v korobsi');
readln(l2);
writeln('daiamtr oci catelita');
readln(d);
writeln('diametr opornoi poverxni');
readLn(d1);
writeln('kofisient U');
readln(u);
writeln('vedit kofisient U1');
readln(u1);
writeln('Nm');
read(Nm);
{Programa}
lamda:=(L-d)/L ;
sig1:=Mmax*u*u1*Nm/(r*q*d*ll);
sig2:=(Mmax*u*u1*Nm)/(r1*q*d*l2) ;
sig3:=((Mmax*u*u1*Nm)/(r*q*3.14*(sqr(d)-sqr(d1))))*1.5*1 ;
sig4:=(2*Mmax*u*u1*Nm)/(r*3.14*(sqr(1.15*r1)-sqr(1.1*r)))*1.5*(z/z0) ;
sigx:=(sig1+sig2+sig3+sig4 )/4 ;
M:=sqrt((3*(1+0.15)*Mmax*u1*u*0.9)/sigx*z*q*L*(1-sqr(lamda)*lamda)*3.14*1) ;
Writeln('modyl=',M:3:3,'MM');
if sigx>550 then
writeln(' *** error ***pomilka peregryska****',sigx);
writeln( 'modul tisku=',sigx:5:2,'Mpa');
{///////////////1//////////////}
if sig1>70 then
writeln ('*** error ***pomilka peregryska****',sig1:5:2,'MPa' );
writeln('tisk na vis satelita v shesterni =',sig1:5:5,'(MPa)');
{//////////////////2//////////////}
if sig2>70 then
writeln ('*** error ***pomilka peregryska****',sig2:5:2,'MPa' );
writeln('tisk na vis satelita v kopobsi =',sig2:5:2,'(MPa)');
{/////////////////3////////////////}
if sig3>70 then
writeln ('*** error ***pomilka peregryska****',sig3:5:2,'MPa' );
writeln('Tisk na torets satelita=',sig3:5:2,'(MPa)');
{///////////////////4////////////////}
if sig4>70 then
writeln ('*** error ***pomilka peregryska****',sig4:5:2,'MPa' );
writeln('tisk na torsi shesterni =',sig4:5:2,'(MPa)');
readln;
end.
1.7 Перевірка програми виведення оброблених результатів Рис1.10
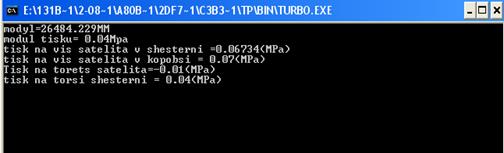
Рис1.10 Вихідні дані
Розробка програми для розв’зання систем лінійних рівнянь
Теоретичні відомості
Одним з основних напрямів використання комп'ютерів є накопичення і обробка даних - різних таблиць, довідників, словників і іншої інформації. Для представлення такої інформації в програмі зручно використовувати масиви. Як правило, обробка таких даних здійснюється поодинці і тому ж закону, для чого зручно використовувати циклічні алгоритми.
Метод Гауса вважається точним методом розв’язання систем лінійних рівнянь. Точність розв’язання залежить у даному випадку тільки від точності виконання математичних операцій
Нехай задано систему
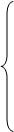
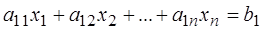 ,
,
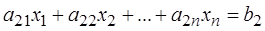 , (2.1)
, (2.1)
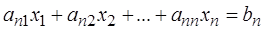 ,
,
або в матричній формі
А*х = b, (2.2)
де
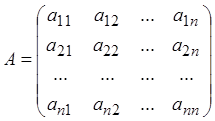 ,
, 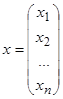 ,
, 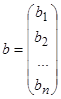 , (2.3)
, (2.3)
де А – матриця системи,
х – стовпець невідомих,
b – стовпець вільних членів.
Суть методу Гауса полягає в тому, що система (1.1) шляхом послідовного виключення невідомих приводиться до системи з трикутною матрицею, із якої потім визначаються значення невідомих.
В масив ми об'єднуємо кінцеву послідовність компонентів одного типу і даємо їм загальне ім'я. Кожен окремий компонент масиву називається елементом. Кількість елементів називається розміром масиву. Тип елементів визначає тип масиву. Розмір і тип масиву указуються при його описі, причому розмір може бути вказаний або конкретним значенням, або раніше певною константою. Номер елементу називається індексом. Індекси можуть бути цілими позитивними константами або цілими змінними. Щоб звернутися до деякого елементу масиву, потрібно поряд з ідентифікатором масиву в дужках вказати індекс елементу.
Але часто дані можуть бути організовані у вигляді таблиці (матриці), де те, що має в своєму розпорядженні кожну змінну визначається номером рядка і номером стовпця. Наприклад, місце в залі для глядачів задається вказівкою номера ряду і номером місця в цьому ряду. Такі дані зручно описати як двовимірний масив. На відміну від одновимірного масиву кожному елементу двовимірного масиву відповідає пара індексів. Перший індекс - це номер рядка, а другою - номер стовпця, де розташований елемент масиву.
Відмітною особливістю масивів є та обставина, що всі їх компоненти суть дані одного типу (можливо, структурованого); ці компоненти можна легко упорядкувати і забезпечити доступ до будь-якого з них простою вказівкою його порядкового номера.
Для розв’язання систем лінійних алгебраїчних рівнянь можна використати ітераційні методи, які дозволяють визначити вектор невідомих як границю нескінченної послідовності векторів невідомих, що обчислюються за деяким однотипним процесом, який називається процесом ітерації.
Одним із найрозповсюдженіших ітераційних методів, що відрізняється простотою та легкістю програмування, є метод Гауса.
Для збіжності ітераційного процесу достатньо, щоб модулі діагональних коефіцієнтів для кожного рівняння системи були не менше суми модулів решти його коефіцієнтів:
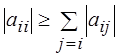 , j=1,2,…n (2.4)
, j=1,2,…n (2.4)
При цьому хоча б для одного рівняння нерівність повинна виконуватись суворо. Ці умови є достатні для збіжності методу, але вони не є необхідними, тобто для деяких систем ітерації збігаються і при порушенні даної умови.
Дата: 2019-05-29, просмотров: 292.