Код Хэмминга – систематический код, то есть состоящий из информационных и корректирующих символов, расположенных по строго определенной системе, имеющих одинаковую длину и всегда занимающих строго определенные места в кодовых комбинациях.
Предложенные Хэммингом регулярные методы построения кодов, корректирующих ошибки, имеют фундаментальное значение. Они демонстрируют инженерам практическую возможность достижения пределов, на которую указывали законы теории информации. Эти коды нашли практическое применение при создании компьютерных систем. Работа Хэмминга привела к решению проблемы более плотной упаковки для конечных полей. Он ввел в научный обиход важнейшие понятия теории кодирования – расстояние Хэмминга между кодовыми комбинациями в векторном пространстве, определяемом для двоичных кодов как количество позиций этих комбинаций с различными символами, и границы Хэмминга для исправляющей способности блочных корректирующих кодов. Граница Хэмминга для двоичных кодов рассчитывается по следующей формуле:
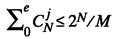
В этом выражении число ошибок e может быть исправлено корректирующим блочным кодом длиной N, имеющим М кодовых комбинаций (CjN – биномиальный коэффициент)[3].
Работа Хэмминга сыграла ключевую роль в последующем развитии теории кодирования и стимулировала обширные исследования, выполненные в последующие годы.
Коды Хэмминга позволяют не только обнаружить наличие ошибки, но и место ее нахождения и, следовательно, дают возможность ее исправить. Однако коды Хэмминга обладают меньшей избыточностью (по сравнению с кодированием по методу четности-нечетности), т.е. количеством дополнительных контрольных разрядов.
При передаче кода может быть искажен или не искажен любой символ. Если длина кода – n символов, то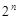 
– полное количество комбинаций кода. По методике Хэмминга можно определить число информационных символов кода, обнаруживающего и корректирующего одиночную ошибку следующим образом:
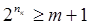
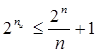, где
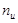– число информационных символов в коде;
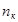– число контрольных символов;
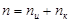– длина кода Хемминга.
Соотношение n, 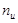и 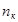для кода Хэмминга можно представить в виде таблицы:
Таблица 2.2.a
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|
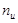
| 0 | 0 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 11 |
|
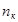
| 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
Предположим, что имеется код, содержащий m информационных и k контрольных разрядов. Все разряды, включая контрольные, разбиваются на k групп по определенным правилам, о которых будет сказано ниже. Каждая группа, содержащая один контрольный разряд, проверяется на четность. Пусть были проведены все k проверок. Если результат данной проверки свидетельствует об отсутствии ошибки, то записывается 0, если есть ошибка, то записывается 1. В результате получается последовательность, состоящая из k нулей и единиц. При отсутствии ошибки в коде получается последовательность нулей. Полученное k-разрядное двоичное число может содержать 2k различных комбинаций нулей и единиц. С помощью этой информации нужно определить ошибочный разряд в коде, содержащем m+k разрядов. Для того чтобы это было возможно должно выполняться неравенство:
2k (m+k+1)
Определить максимальное значение m для данного k можно из следующей таблицы.
| n | 1,2,3,4… | 8,…,15 | 16,…31 | … |
| m | 0,0,1,1… | 4,…11 | 11,…26 | … |
| k | 1,2,2,3 | 4…4 | 5…5 | … |
Из таблицы видно, для 16-ти разрядного числа требуется 5 контрольных разрядов. В качестве сравнения, в случае модифицированного метода четности потребовалось бы 8 контрольных разрядов. Позиции контрольных разрядов в методе Хэмминга определены заранее, это разряды 1,2,4,8,… Разряды, входящие в каждую группу проверки представлены в следующей таблице (1-й разряд в каждой группе является контрольным).
| номер группы проверки | проверяемые разряды |
| 1 | 1,3,5,7,9,11,13,15,… |
| 2 | 2,3,6,7,10,11,14,15,18,19,22,23,… |
| 3 | 4,5,6,7,12,13,14,15,20,21,22,23,… |
| 4 | 8,9,10,11,12,13,14,15,24,… |
Из таблицы видно, что если, например код Хэмминга содержит 9 разрядов, включая контрольные, то 1-я группа проверки содержит 1,3,5,7,9 разряды. 2-я группа проверки содержит 2,3,6,7 разряды. 3-группа проверки содержит 4,5,6,7 разряды и 4-я группа – 8,9 разряды. Каждой группе проверки приписывается 1, если проверка на четность обнаруживает ошибку и 0, если ошибки нет. Полученное двоичное число дает номер ошибочного разряда.
Код Хэмминга имеет существенный недостаток: при обнаружении любого числа ошибок он исправляет лишь одиночные ошибки. Например, избыточность семиэлементного кода Хэмминга равна 0,43. При увеличении значности кодовых комбинаций увеличивается число проверок, но уменьшается избыточность кода. К тому же код Хэмминга не позволяет обнаружить групповые ошибки. Длина пакета ошибок представляет собой увеличенную на единицу разность между именами старшего и младшего ошибочных элементов.
Рассмотрим в качестве примера 5-ти разрядное двоичное число 10011. В этом случае, как следует из вышеприведенной таблицы, 1-я группа проверки состоит из 1,3, и 5-го разрядов. 2-я группа проверки состоит из 2 и 3-го разряда. 3-я группа проверки состоит из 4 и 5-го разрядов. Результат проверки на четность 1-й группы дает 0 (101), проверка 2-й группы дает 0 (00), проверка 3-й группы дает 0 (11).
k1 = 1 + 0 + 1 = 0 – нет ошибки;
k2 = 0 + 0 =0 – нет ошибки;
k3 = 1 + 1 = 0 – нет ошибки.
Таким образом, данное число не содержит ошибки. Искусственно введем ошибку, заменив, например, 4-й разряд на 0. В этом случае 1, 2 и 3-я проверки дадут соответственно 0, 0, 1.
k1 = 1 + 0 + 1 = 0 – нет ошибки;
k2 = 0 + 0 =0 – нет ошибки;
k3 = 0 + 1 = 1 – ошибка.
Полученное двоичное число 100 дает номер ошибочного разряда, т.е. 4.
Машина Поста
«Внешний вид» машины Поста
Машина Поста не есть реально существующее, сделанное кем-то устройство; поэтому слова «внешний вид» и взяты в кавычки. Машина Поста, как и ее близкий родственник - машина Тьюринга, - представляет собой мысленную конструкцию, существующую лишь в нашем воображении (хотя ее в принципе и можно было бы изготовить «в металле»). Именно это имеют в виду, когда говорят о машинах Поста и Тьюринга, что они суть «абстрактные» вычислительные машины. И подобно тому, как можно выучиться считать на счетах или на логарифмической линейке, не имея перед собой этих приборов, а, пользуясь лишь их описаниями и представляя их себе мысленно, так же и мы научимся вычислять на машине Поста.
Машина Поста состоит из ленты и каретки (называемой также считывающей и записывающей головкой).
Лента бесконечна и разделена на секции одинакового размера: для наглядности ленту будем считать расположенной горизонтально (рис. 13).
Бесконечность ленты находится в противоречии со сделанным выше утверждением, что машину Поста можно было бы в принципе построить. Дело в том, что мы объявили ленту бесконечной лишь для простоты изложения. С тем же успехом можно было бы предположить, что лента не бесконечная, а лишь неограниченно растущая в обе стороны: например, можно было бы считать, что лента наращивается на одну секцию, как только каретка доходит до конца ленты и должна двигаться дальше, или считать, что за каждую единицу времени слева и справа нарастает по одной секции. Однако будет удобнее считать, что все секции слева и справа уже наросли, и тем самым, хотя и в ущерб реальности, полагать ленту бесконечной в обе стороны.
Порядок, в котором расположены секции ленты, подобен порядку, в котором расположены все целые числа. Поэтому естественно ввести на ленте «целочисленную систему координат», занумеровав секции целыми числами ..., -3,-2,-1,0,1, 2,3, ... (рис. 14).
Мы будем считать, что система координат жестко сопоставлена с лентой, и получим, таким образом, возможность указывать какую-либо секцию ленты, называя ее порядковый номер, или координату. (Иногда, впрочем, бывает удобно наряду с основной, «постоянной» системой координат, ввести еще вспомогательную, «временную», сдвинутую по отношению к первоначальной)
В каждой секции ленты может быть либо ничего не записано (такая секция называется пустой), либо записана метка V (тогда секция называется отмеченной) (рис. 15).
Информация о том, какие секции пусты, а какие отмечены, образует состояние ленты. Иными словами, состояние ленты — это распределение меток по ее секциям. Как мы далее увидим, состояние ленты меняется в процессе работы машины.
Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной секции ленты на этом и следующих чертежах каретка изображена в виде зачерненного квадрата); говорят, что каретка обозревает эту секцию, или держит ее в поле зрения.
Информация о том, какие секции пусты, а какие отмечены и где стоит каретка, образует состояние машины Поста.
Таким образом, состояние машины слагается из состояния ленты и указания номера той секции, которую обозревает каретка. За единицу времени (которую мы будем называть шагом) каретка может сдвинуться на одну секцию влево или вправо. Кроме того, каретка может поставить (напечатать) или уничтожить (стереть) метку на той секции, против которой она стоит, а также распознать, стоит или нет метка в обозреваемой ею секцией[2].
Программа машины Поста
Работа машины Поста состоит в том, что каретка передвигается вдоль ленты и печатает или стирает метки. Эта работа происходит по инструкции определенного вида, называемой программой. Для машины Поста возможно составление различных программ. Посмотрим, как устроена программа.
Каждая программа машины Поста состоит из команд. Командой машины Поста будем называть выражение, имеющее один из следующих шести видов (буквы i, j, j1, j2 означают всюду натуральные числа 1, 2, 3, 4, 5, …):
Первый вид. Команды движения вправо.
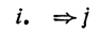
Второй вид. Команды движения влево.
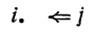
Третий вид. Команды печатания метки.
Четвертый вид. Команды стирания метки.
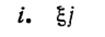
Пятый вид. Команды передачи управления.
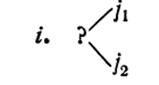
Шестой вид. Команды остановки.
Например,
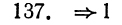
является командой движения вправо,
- командой передачи управления, а
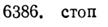
-командой остановки.
Число i, стоящее в начале команды, называется номером команды. Так, у приведенных только что команд номера соответственно 137, 25 и 6386. Число j, стоящее в конце команды (а у команд передачи управления - каждое из чисел j1, и j2), будем называть отсылкой (при этом в команде передачи управления j1—верхней, а j2 — нижней отсылкой). У команд остановки нет отсылки. Так, у приведенных только что команд отсылками служат числа 1, 32, 25, причем 32 —верхняя отсылка, а 25 — нижняя отсылка.
Программой машины Поста будем называть конечный непустой (т. е. содержащий хотя бы одну команду) список команд машины Поста, обладающий следующими двумя свойствами:
1) На первом месте в этом списке стоит команда с номером 1, на втором месте (если оно есть) – команда с номером 2 и т. д.; вообще на k-м месте стоит команда с номером k.
2) Отсылка любой из команд списка совпадает с номером некоторой (другой или той же самой) команды списка (более точно: для каждой отсылки каждой команды списка найдется в.списке такая команда, номер которой равен рассматриваемой отсылке).
Например, следующий список будет программой машины Поста:
А эти два списка не будут программами машины Поста, хотя и составлены из команд машины Поста:
Для наглядности программы машины Поста мы будем записывать столбиком. Число команд программы называется длиной программы[1].
Работа машины Поста
Чтобы машина Поста начала работать, надо задать, во-первых, некоторую программу, а во-вторых, некоторое ее (машины) состояние, т. е. как-то расставить метки по секциям ленты (в частности, можно все секции оставить пустыми) и поставить каретку против одной из секций. Как правило, мы будем предполагать, что в начальном (т.е. в задаваемом вначале) состоянии машины каретка ставится всегда против секции с номером (координатой) нуль. При таком соглашении начальное состояние машины полностью определено состоянием ленты.
Как уже говорилось, программа является той инструкцией, на основании которой работает машина. Работа машины на основании заданной программы (и при заданном начальном состоянии) происходит следующим образом. Машина приводится в начальное состояние и приступает к выполнению первой команды программы. Эта команда выполняется за один шаг, после чего машина приступает к выполнению той команды, номер которой (назовем его а) равен отсылке (одной из отсылок, если их две) первой команды. Эта команда также выполняется за один шаг, после чего начинается выполнение команды, номер которой равен отсылке команды с номером а. Вообще каждая команда выполняется за один шаг, а переход от выполнения одной команды к выполнению другой происходит по следующему правилу: пусть на k-м шаге выполнялась команда с номером i, тогда, если эта команда имеет единственную отсылку j, то на k+1-м шаге выполняется команда с номером j; если эта команда имеет две отсылки j1 и j2, то на k+1-м шаге выполняется одна из двух команд – с номером j1 или с номером; если, наконец, выполняющаяся на k-м шаге команда вовсе не имеет отсылки, то на k + 1-м шаге и на всех последующих шагах не выполняется никакая команда: машина останавливается. Осталось объяснить, что значит выполнить команду и какая из отсылок - при наличии двух - выбирается в качестве номера следующей команды.
Выполнение команды движения вправо состоит а том, что каретка сдвигается на одну секцию вправо. Выполнение команды движения влево состоит в том, что каретка сдвигается на одну секцию влево. Выполнение команды печатания метки состоит в том, что каретка ставит метку на обозреваемой секции; выполнение этой команды возможно лишь в том случае, если обозреваемая перед началом выполнения команды секция пуста; если же на обозреваемой секции уже стоит метка, команда считается невыполнимой. Выполнение команды стирания метки состоит в том, что каретка уничтожает метку в обозреваемой секции; выполнение этой команды возможно лишь в том случае, если обозреваемая секция отмечена; если же на обозреваемой секции и так нет метки, команда считается невыполнимой. Выполнение команды передачи управления с верхней отсылкой j1 и нижней отсылкой j2 никак не изменяет состояния машины: ни одна из меток не уничтожается и не ставится, и каретка также остается неподвижной (машина делает, так сказать, «шаг на месте»); однако если секция, обозреваемая перед началом выполнения этой команды, была пуста, то следующей должна выполняться команда с номером j1, если же эта секция была отмечена, следующей должна выполняться команда с номером j2 (роль команды передачи управления сводится, следовательно, к тому, что каретка во время выполнения этой команды как бы «распознает», стоит ли перед ней метка). Выполнение команды остановки тоже никак не меняет состояния машины и состоит в том, что машина останавливается.
Если теперь, задавшись программой и каким-либо начальным состоянием, пустить машину в ход, то осуществится один из следующих трех вариантов:
1) В ходе выполнения программы машина дойдет до выполнения невыполнимой команды (печатания метки в непустой секции или стирания метки в пустой секции); выполнение программы тогда прекращается, машина останавливается; происходит так называемая безрезультатная остановка.
2) В ходе выполнения программы машина дойдет до выполнения команды остановки; программа в этом случае считается выполненной, машина останавливается; происходит так называемая результативная остановка.
3) В ходе выполнения программы машина не дойдет до выполнения ни одной из команд, указанных в первых двух вариантах; выполнение программы при этом никогда не прекращается, машина никогда не останавливается; процесс работы машины происходит бесконечно[5].
Дата: 2019-05-29, просмотров: 154.
