Каждый член ряда (3) удовлетворяет граничным условиям на контуре рассматриваемой пластины, т.е. условиям равенства нулю в точках на контуре величины прогиба пластины и изгибающих моментов:
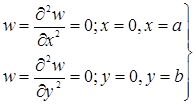 (4)
(4)
Уравнение, устанавливающее сочетание нагрузок Т1 и Т2, при котором свободно опёртая по контуру прямоугольная пластина может потерять устойчивость (8)
Подставляя формулу (3) в дифференциальное уравнение (1), Получим
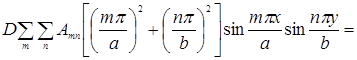
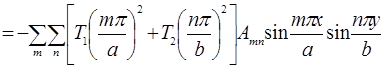
или
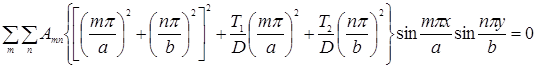 (5)
(5)
Рассматриваемая пластина может потерять устойчивость при таком сочетании нагрузок Т1 и Т2, при котором какая-либо из скобок, входящих в выражение (5), обратится в нуль.
При этом соответствующее Аmn может стать отличным от нуля и форма потери устойчивости пластины будет
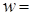
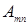
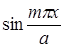
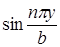 (6)
(6)
Таким образом, эйлерово сочетание нагрузок Т1 и Т2 определится из условия:
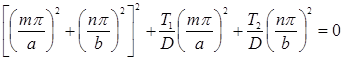
Учитывая обозначения (2), получим
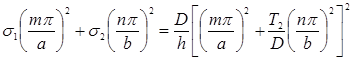 (7)
(7)
Или
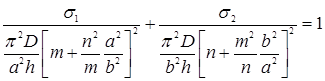 (8)
(8)
Устойчивость прямоугольной свободно опёртой по контуру пластины, одинаково сжатой в обоих направлениях. (11)
Для дальнейшего исследования полезно выражение (7) переписать следующим образом:
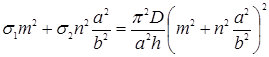 (9)
(9)
При различных комбинациях чисел "m" и "n" мы имеем, на основании выражения (9) линейную зависимость между напряжениями σ1 и σ2.
Будем откладывать на оси абсцисс некоторой системы координатных осей напряжение σ1, а на оси ординат-напряжение σ2 (рис.2). Тогда любой точке плоскости будет соответствовать некоторая комбинация напряжений σ1 и σ2
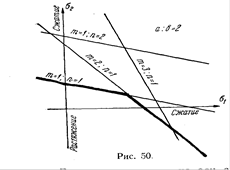
 Рис.2
Рис.2
Рассматривая пластину с определенным отношением сторон а: b, можем, задаваясь различными "m" и "n", построить ряд прямых по уравнениям (9). Область тех напряжений, при которых пластина не теряет устойчивости, будет ограничена ближайшими к началу координат участками всех построенных прямых различных "m" и "n".
Легко убедиться, что для определения этих участков нужно построить лишь прямые, соответствующие различным "m" при n=1 и различным "n" при m=1.
Если σ1=σ2., т.е. пластина одинаково сжата в обоих направлениях, то на основании выражения (9) получим
σ1=σ2 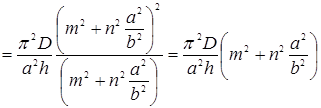 (10)
(10)
Правая часть формулы (10) растет при увеличении чисел "m" и "n". Поэтому в таком случае для разыскания эйлеровых значений сжимающих напряжений следует в формуле (10) положить m = n =1. Тогда получим
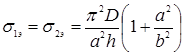 (11)
(11)
где 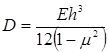 - цилиндрическая жесткость пластины.
- цилиндрическая жесткость пластины.
Следовательно, одинаково сжатая в двух пластина теряет устойчивость с образованием одной полуволны независимо от величины отношения а: b.
Расчёт эйлеровых значений сжимающих усилий прямоугольной свободно опёртой по контуру пластины, одинаково сжатой в обоих направлениях.
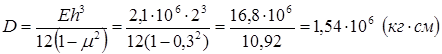
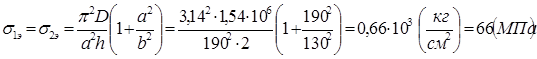
Дата: 2019-05-29, просмотров: 292.