Исходные данные
| № п/п | Размер пластины (a), м | Размер пластины (b), м | Модуль упругости материала Е ·103МПа | Толщина пластины (h), м |
| 19 | 1.90 | 1,30 | 210 | 0.020 |
Дифференциальное уравнение нейтрального равновесия прямоугольной пластины, сжатой в двух взаимно перпендикулярных направлениях (1), (2)
Начнем изучение устойчивости пластин со случая, когда на свободно опертую прямоугольную пластину действуют сжимающие напряжения в двух взаимно перпендикулярных направлениях (рис.1).
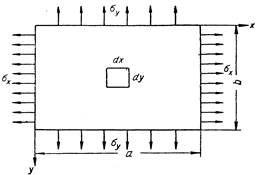
Рис.1
Пусть σ1 - абсолютная величина сжимающего напряжения, действующего в направлении оси ох; σ2-абсолютная величина сжимающего напряжения, действующего в направлении оси оу; "а" и "b"-размеры пластины в плане; "h"-толщина пластины.
Тогда дифференциальное уравнение нейтрального равновесия рассматриваемой пластины будет:
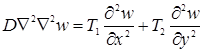 (1)
(1)
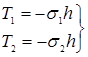 (2)
(2)
Задание формы упругой поверхности свободно опертой пластины при потере устойчивости в виде двойного тригонометрического ряда (3)
Упругая поверхность свободно опертой пластины при потере устойчивости в самом общем виде может быть представлена тригонометрическим рядом:
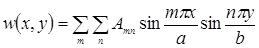 (3)
(3)
Граничные условия на кромках рассматриваемой прямоугольной свободно опёртой по контуру пластины (4)
Каждый член ряда (3) удовлетворяет граничным условиям на контуре рассматриваемой пластины, т.е. условиям равенства нулю в точках на контуре величины прогиба пластины и изгибающих моментов:
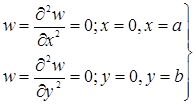 (4)
(4)
Уравнение, устанавливающее сочетание нагрузок Т1 и Т2, при котором свободно опёртая по контуру прямоугольная пластина может потерять устойчивость (8)
Подставляя формулу (3) в дифференциальное уравнение (1), Получим
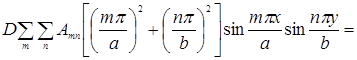
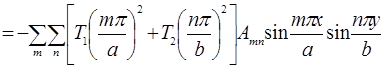
или
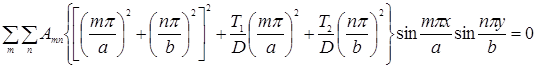 (5)
(5)
Рассматриваемая пластина может потерять устойчивость при таком сочетании нагрузок Т1 и Т2, при котором какая-либо из скобок, входящих в выражение (5), обратится в нуль.
При этом соответствующее Аmn может стать отличным от нуля и форма потери устойчивости пластины будет
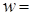
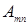
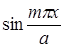
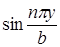 (6)
(6)
Таким образом, эйлерово сочетание нагрузок Т1 и Т2 определится из условия:
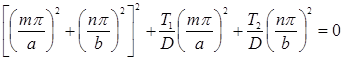
Учитывая обозначения (2), получим
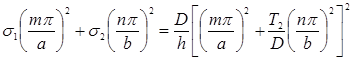 (7)
(7)
Или
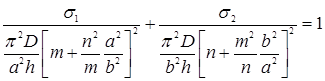 (8)
(8)
Расчёт эйлеровых значений сжимающих усилий прямоугольной свободно опёртой по контуру пластины, одинаково сжатой в обоих направлениях.
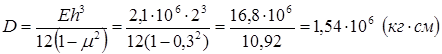
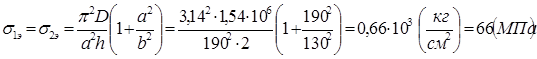
Устойчивость прямоугольной свободно опёртой по контуру пластины, сжатой в одном направлении вдоль длинной стороны пластины. (12)
Если пластина сжата лишь в одном направлении, то ее эйлерову нагрузку можно найти из общих зависимостей предыдущего параграфа, положив в них σ2=0. На основании формулы (9) получим
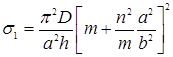 (12)
(12)
Устойчивость пластин при действии касательных напряжений. Расчётная схема (Рис.6)
Рассмотрим свободно опертую пластину, находящуюся в условиях чистого сдвига под действием касательных напряжений τ (Рис.6).
Сдвигающие усилия на единицу длины пластины будут 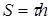
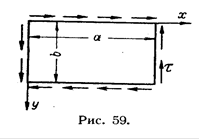
 Рис.6
Рис.6
Заключение
Анализ прямоугольных пластин позволяет сделать вывод об их устойчивости и как следствие прочности всей судовой конструкции. Полученные значения касательных и эйлеровых напряжений допустимы.
Список литературы
Основная литература
1. Ипатовцев Ю.Н., Короткин Я.И. Строительная механика и прочность корабля: Учебник. Л.: Cудостроение, 1991
2. Короткин Я.И., Ростовцев Д.М., Сиверс Н.Л. Прочность корабля: Учебник. Л.: Судостроение, 1974
3. Постнов В.А. и др. Строительная механика корабля и теория упругости: Учебник: в 2-х томах. Л.: Cудостроение, 1987
Дополнительная литература
1. Архангородский А.Г., Беленький Л.М. Аналитический метод проектирования корпуса корабля, Л.: Судпромгиз. 1961
2. Короткин Я.И., Локшин А.З., Сиверс Н.Л. Изгиб и устойчивость стержней и стержневых систем: Учебное пособие, М.Л. .: Машгиз, 1953
3. Короткин Я.И., Локшин А.З., Сиверс Н.Л. Изгиб и устойчивость пластин и круговых цилиндрических оболочек: Учебное пособие, Л.: Судпромгиз, 1955
4. Крыжевич Г.Б. Основы расчётов надёжности судовых конструкций: Учебное пособие, Санкт-Петербург.: СПбГМТУ, 1995
5. Локшин А.З., Рябов Л.И. Судовые кничные соединения, Л.: Cудостроение, 1973
6. Попов Ю.Н. и др. Прочность судов, плавающих во льдах, Л.: Cудостроение, 1967
7. Справочник по строительной механике корабля: в 3-х томах / Под ред. акад. Ю.А. Шиманского. Л.: Судпромгиз. 1960
8. Справочник по строительной механике корабля: в 3-х томах/Бойцов Г.В., Палий О.М., Постнов В.А., Чувиковский В.С. Л.: Cудостроение, 1982
9. Чибиряк И.М. Методические указания к выполнению курсовой работы по конструкции корпуса корабля. Владивосток, изд. ДВПИ им.В. В. Куйбышева, 1977.
Исходные данные
| № п/п | Размер пластины (a), м | Размер пластины (b), м | Модуль упругости материала Е ·103МПа | Толщина пластины (h), м |
| 19 | 1.90 | 1,30 | 210 | 0.020 |
Дифференциальное уравнение нейтрального равновесия прямоугольной пластины, сжатой в двух взаимно перпендикулярных направлениях (1), (2)
Начнем изучение устойчивости пластин со случая, когда на свободно опертую прямоугольную пластину действуют сжимающие напряжения в двух взаимно перпендикулярных направлениях (рис.1).

Рис.1
Пусть σ1 - абсолютная величина сжимающего напряжения, действующего в направлении оси ох; σ2-абсолютная величина сжимающего напряжения, действующего в направлении оси оу; "а" и "b"-размеры пластины в плане; "h"-толщина пластины.
Тогда дифференциальное уравнение нейтрального равновесия рассматриваемой пластины будет:
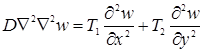 (1)
(1)
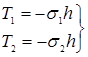 (2)
(2)
Задание формы упругой поверхности свободно опертой пластины при потере устойчивости в виде двойного тригонометрического ряда (3)
Упругая поверхность свободно опертой пластины при потере устойчивости в самом общем виде может быть представлена тригонометрическим рядом:
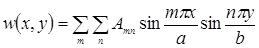 (3)
(3)
Дата: 2019-05-29, просмотров: 282.