Нехай 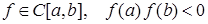 і відомо, що рівняння (1) має єдиний корінь
і відомо, що рівняння (1) має єдиний корінь 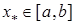 . Покладемо a0=a, b0=b, x0=(a0+b0)/2. Якщо
. Покладемо a0=a, b0=b, x0=(a0+b0)/2. Якщо 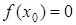 , то
, то 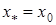 . Якщо
. Якщо 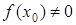 , то покладемо
, то покладемо
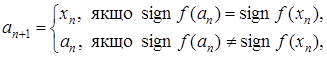 (2)
(2)
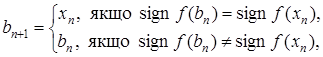 (3)
(3)
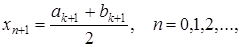 (4)
(4)
і обчислимо 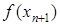 . Якщо
. Якщо 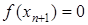 , то ітераційний процес зупинимо і будемо вважати, що
, то ітераційний процес зупинимо і будемо вважати, що 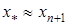 . Якщо
. Якщо 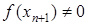 , то повторюємо розрахунки за формулами (2) – (4).
, то повторюємо розрахунки за формулами (2) – (4).
З формул (2), (3) видно, що 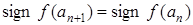 і
і 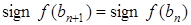 . Тому
. Тому 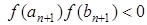 , а отже шуканий корінь
, а отже шуканий корінь 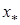 знаходиться на проміжку
знаходиться на проміжку 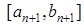 . При цьому має місце оцінка збіжності
. При цьому має місце оцінка збіжності
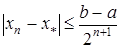 . (5)
. (5)
Звідси випливає, що кількість ітерацій. які необхідно провести для знаходження наближеного кореня рівняння (1) з заданою точністю e задовольняє співвідношенню
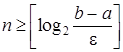 . (6)
. (6)
де [c] - ціла частина числа c.
Серед переваг даного методу слід відзначити простоту реалізації та надійність. Послідовність {xn} збігається до кореня 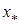 для довільних неперервних функцій f(x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.
для довільних неперервних функцій f(x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.
Метод простої ітерації
Метод простої ітерації застосовується до розв’язування нелінійного рівняння виду
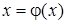 . (7)
. (7)
Перейти від рівняння (1) до рівняння(7) можна багатьма способами, наприклад, вибравши
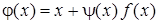 , (8)
, (8)
де 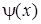 - довільна неперервна функція.
- довільна неперервна функція.
Вибравши нульове наближення x0, наступні наближення знаходяться за формулою
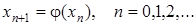 . (9)
. (9)
Наведемо достатні умови збіжності методу простої ітерації.
Теорема 1. Нехай для вибраного початкового наближення x0 на проміжку
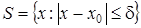 (10)
(10)
функція j(x) задовольняє умові Лівшиця
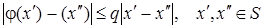 (11)
(11)
де 0<q<1, і виконується нерівність
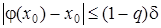 . (12)
. (12)
Тоді рівняння (7) має на проміжку S єдиний корінь 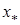 , до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю
, до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю
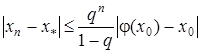 . (13)
. (13)
Зауваження: якщо функція j(x) має на проміжку S неперервну похідну 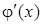 , яка задовольняє умові
, яка задовольняє умові
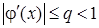 , (14)
, (14)
то функція j(x) буде задовольняти умові (11) теореми 1.
З (13) можна отримати оцінку кількості ітерацій. які потрібно провести для знаходження розв’язку задачі (7) з наперед заданою точністю e:
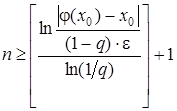 . (15)
. (15)
Наведемо ще одну оцінку. що характеризує збіжність методу простої ітерації:
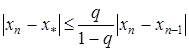 . (16)
. (16)
Метод релаксації
Для збіжності ітераційного процесу (9) суттєве значення має вибір функції j(x). Зокрема, якщо в (8) вибрати 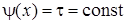 , то отримаємо метод релаксації.
, то отримаємо метод релаксації.
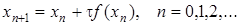 , (17)
, (17)
який збігається при
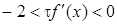 . (18)
. (18)
Якщо в деякому околі кореня виконуються умови
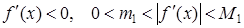 , (19)
, (19)
то метод релаксації збігаються при 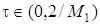 . Збіжність буде найкращою при
. Збіжність буде найкращою при
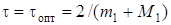 . (20)
. (20)
При такому виборі t для похибки 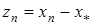 буде мати місце оцінка
буде мати місце оцінка
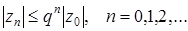 , (21)
, (21)
де 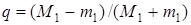 .
.
Кількість ітерацій, які потрібно провести для знаходження розв’язку з точністю e визначається нерівністю
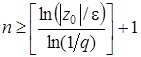 . (22)
. (22)
Зауваження: якщо виконується умова 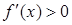 , то ітераційний метод (17) потрібно записати у вигляді
, то ітераційний метод (17) потрібно записати у вигляді 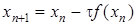 .
.
Метод Ньютона
Метод Ньютона застосовується до розв’язування задачі (1), де f(x) є неперервно-диференційованою функцією. На початку обчислень вибирається початкове наближення x0. Наступні наближення обчислюються за формулою
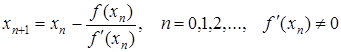 . (23)
. (23)
З геометричної точки зору xn+1 є значенням абсциси точки перетину дотичної до кривої y=f(x) в точці (xn, f(xn)) з віссю абсцис. Тому метод Ньютона називають також методом дотичних.
Теорема 2. Якщо 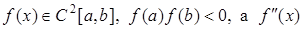 не змінює знака на [a, b], то виходячи з початкового наближення
не змінює знака на [a, b], то виходячи з початкового наближення 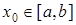 , що задовольняє умові
, що задовольняє умові 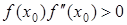 , можна обчислити методом Ньютона єдиний корінь
, можна обчислити методом Ньютона єдиний корінь 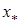 рівняння (1) з будь-якою степінню точності.
рівняння (1) з будь-якою степінню точності.
Теорема 3. Нехай 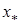 - простий дійсний корінь рівняння (1) і
- простий дійсний корінь рівняння (1) і 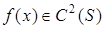 , де
, де 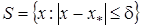 ,
,
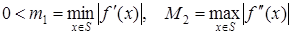 , (24)
, (24)
причому
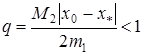 . (25)
. (25)
Тоді для 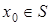 метод Ньютона збігається, причому для похибки справедлива оцінка
метод Ньютона збігається, причому для похибки справедлива оцінка
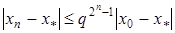 . (26)
. (26)
З оцінки (26) видно, що метод Ньютона має квадратичну збіжність, тобто похибка на (n+1) – й ітерації пропорційна квадрату похибки на n-й ітерації.
Модифікований метод Ньютона
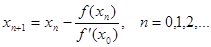 (27)
(27)
дозволяє не обчислювати похідну 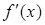 на кожній ітерації, а отже і позбутися можливого ділення на нуль. Однак цей алгоритм має тільки лінійну збіжність.
на кожній ітерації, а отже і позбутися можливого ділення на нуль. Однак цей алгоритм має тільки лінійну збіжність.
Кількість ітерацій, які потрібно провести для знаходження розв’язку задачі (1) з точністю e задовольняє нерівності
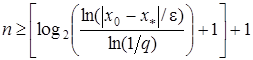 . (28)
. (28)
Дата: 2019-05-29, просмотров: 434.