Исходная модель Келдыша. Цель этого раздела состоит в аналитическом приближенном решении нестационарного уравнения Шредингера, описывающего поведение атомарной системы во внешнем электромагнитном поле:
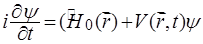 , (8)
, (8)
Здесь 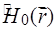 - невозмущенный гамильтониан атомарной системы, а величина
- невозмущенный гамильтониан атомарной системы, а величина 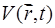 представляет собой потенциал взаимодействия атомарной системы с внешним электромагнитным полем. Предполагаются известными собственные функции и собственные значения энергии стационарного гамильтониана:
представляет собой потенциал взаимодействия атомарной системы с внешним электромагнитным полем. Предполагаются известными собственные функции и собственные значения энергии стационарного гамильтониана:
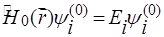 , (9)
, (9)
Точное выражение для амплитуды перехода из начального связанного состояния атома или атомарного иона i в конечное состояние непрерывного спектра f под действием поля лазерного излучения имеет следующий вид ( напомним, что всюду используется атомная система единиц, в которой постоянная Планка, масса электрона и его заряд предполагаются равными единице):
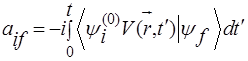 , (10)
, (10)
Здесь конечное состояние описывается точной волновой функцией 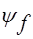 . Выражение (10) эквивалентно исходному нестационарному уравнению Шредингера (8).Вероятность связанно-свободного перехода
. Выражение (10) эквивалентно исходному нестационарному уравнению Шредингера (8).Вероятность связанно-свободного перехода 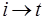 за время t дается квадратом модуля выражения (10).
за время t дается квадратом модуля выражения (10).
Начальное состояние дискретного спектра атома в (10) является невозмущенным и берется из решения уравнения (9).Взаимодействие атома с электронным полем бралось Келдышем в дипольном приближении (так как размеры атома малы по сравнению с длиной волны электромагнитного излучения), используя так называемую калибровку «длины»
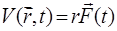 , (11)
, (11)
Здесь F – вектор напряженности электромагнитного поля электромагнитной волны. Предполагалось, что это поле мало по сравнению с характерным атомным полем рассматриваемой атомной системы [2].
Основная идея Келдыша заключалась в том, чтобы заменить неизвестную точную волновую функцию конечного состояния на так называемую волковскую волновую функцию, в которой пренебрегается полем атомного остова и учитывается только поле электромагнитной волны.  В калибровке длины этой волновая функция имеет следующий вид
В калибровке длины этой волновая функция имеет следующий вид
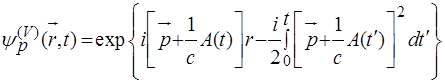 , (12)
, (12)
Здесь векторный потенциал электромагнитного поля связан с напряженностью поля известным соотношением
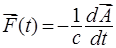 , (13)
, (13)
Указанная волновая функция (11) описывает электрон, колеблющийся в поле электромагнитной волны и имеющий канонический импульс 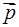 . Средняя (за период колебаний) энергия колебаний Eкол электрона в поле монохроматической электромагнитной волны с частотой
. Средняя (за период колебаний) энергия колебаний Eкол электрона в поле монохроматической электромагнитной волны с частотой 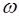 равна
равна 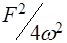 (для поля линейной поляризации) или
(для поля линейной поляризации) или 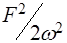 (для поля циркулярной поляризации).
(для поля циркулярной поляризации).
Тогда из (10) для амплитуды связанно-свободного перехода получим приближенное выражение:
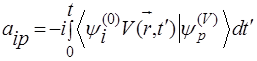 , (14)
, (14)
Энергия фотона лазерного излучения предполагается в подходе Келдыша малой по сравнению с потенциалом ионизации атома (или атомарного иона):
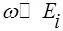 ,
,
Это условие, вместе с условием малости напряженности поля по сравнению с атомной напряженностью, позволяет вычислить аналитически амплитуду перехода, используя метод перевала при интегрировании по времени. Конечно. Такой подход наиболее приемлем для короткодействующего потенциала, для которого только волновая функция S - состояния непрерывного спектра не является плоской волной.
В предположении, что лазерное поле является монохроматическим, т.е. напряженность поля лазерного излучения имеет вид
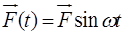 ,
,
Келдыш получил вероятность ионизации в единицу времени. Без учета предэкспоненты для случая поля линейной поляризации эта экспоненциально малая вероятность не зависит от вида атомарного потенциала и имеет универсальный вид:
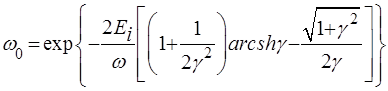 , (15)
, (15)
В полученном выражении введен так называемый параметр адиабатичности (или параметр Келдыша)
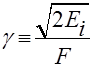 ; (16)
; (16)
Именно он и определяет характер процесса нелинейной ионизации. Еще раз подчеркнем, что полученное выражение справедливо с потенциальной точностью. Для поля циркулярной или эллиптической поляризации аналогичное выражение выглядит более громоздко, и мы его не приводим.
Отметим также, что модель Келдыша калибровочно неинвариантна. Это означает, что выражение для вероятности нелинейной ионизации зависит от того, в какой форме выбирается взаимодействие атома с полем лазерного излучения: в калибровке « длины» или же в калибровке «скорости». Априори неясно, какая из этих форм дает более точные результаты [1].
Туннельный предел
Туннельный режим соответствует низкочастотному пределу, когда параметр адиабатичности много меньше единицы, точнее, 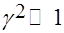 . В этом пределе зависимость вероятности ионизации от частоты поля исчезает, а сама вероятность ионизации в единицу времени (15) приобретает ту же форму, что и для ионизации атома медленно меняющимся со временем электрическим полем
. В этом пределе зависимость вероятности ионизации от частоты поля исчезает, а сама вероятность ионизации в единицу времени (15) приобретает ту же форму, что и для ионизации атома медленно меняющимся со временем электрическим полем 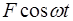 , усредненную по периоду поля:
, усредненную по периоду поля:
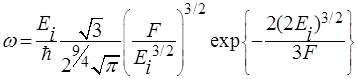 , (17)
, (17)
Основной вклад в эту вероятность дают слагаемые в сумме (15) с очень большими числами N поглощенных фотонов порядка 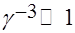 . Эти числа велики по сравнению с минимальным числом
. Эти числа велики по сравнению с минимальным числом 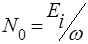 поглощенных фотонов, допустимым законом сохранения энергии. Сумма по числам поглощенных фотонов в окрестности этого значения заменяется непрерывным интегрированием. Так выглядит надпороговое поглощение фотонов электромагнитного излучения в туннельном режиме ионизации [1].
поглощенных фотонов, допустимым законом сохранения энергии. Сумма по числам поглощенных фотонов в окрестности этого значения заменяется непрерывным интегрированием. Так выглядит надпороговое поглощение фотонов электромагнитного излучения в туннельном режиме ионизации [1].
Однако точное решение указанной задачи для ионизации основного состояния атома водорода постоянным электрическим полем с учетом усреднения вероятности по периоду медленно меняющегося поля линейной поляризации дает результат с другой предэкспонентой:
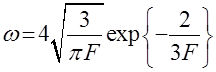 ; (18)
; (18)
Необходимо отметить, что выражение (18) показывает вероятность ионизации одного атома в единицу времени [2].
Механизм ионизации
Важнейшим механизмом рождения зарядов в разрядах является ионизация невозбужденных молекул ударами электронов. Скорость ионизации, т.е. число актов в 1см3 за 1с равно
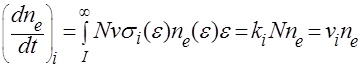 , (19)
, (19)
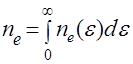 ,
,
где 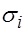
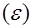 - сечение ионизации электронами с энергией
- сечение ионизации электронами с энергией 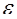 ,
, 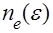 - функция их распределения по энергиям, I- потенциал ионизации,
- функция их распределения по энергиям, I- потенциал ионизации, 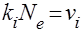 - частота ионизации
- частота ионизации 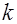 - постоянная, N- число молекул.
- постоянная, N- число молекул.
Частота ионизации является главной характеристикой процесса. Скорость ионизации целесообразно характеризовать ионизационным коэффициентом  - число актов ионизации совершаемых электроном на 1см пути вдоль поля Е.
- число актов ионизации совершаемых электроном на 1см пути вдоль поля Е.
В нашем случае постоянного поля 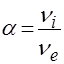 (20), а электронная лавина нарастает вдоль направления движения Х по закону
(20), а электронная лавина нарастает вдоль направления движения Х по закону 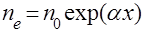 ;
;
Дата: 2019-05-29, просмотров: 330.