Если боковые стороны системы по отношению к растяжению свободны, то нет необходимости следить за шириной ячейки моделирования. Если же на систему наложены периодические граничные условия по двум направлениям, то изменению ширины ячейки моделирования необходимо уделить особое внимание. При растяжении появляются сжимающие в поперечном направлении напряжения и поперечный размер (ширина системы) уменьшается. Если ширину ячейки моделирования не изменять, то появится зазор, который будет увеличиваться со временем - система разорвется в поперечном направлении.

Один из подходов [13] состоит в умножении ширины ячейки моделирования на 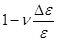, при увеличении длины в  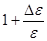раз. Здесь  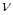примерно равно коэффициенту Пуассона. Этого, однако, может оказаться недостаточно, поэтому, вводят дополнительную оптимизацию поперечного размера системы, основанную на методе Монте-Карло. После каждых ~20 шагов по времени МД предлагается изменение поперечного размера системы. Если в результате этого изменения энергия системы уменьшается, изменение принимается, в противном случае отклоняется. Вследствие этого, точное значение, выбранное для 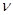, становится некритичным.

В данной работе предложен и используется другой подход, основанный на динамическом уравнении для ширины ячейки моделирования. Выше уже было отмечено, что из-за периодичности в поперечном направлении система имеет топологию цилиндра. Сжимающие в поперечном направлении напряжения приводят к уменьшению боковой поверхности цилиндра и, следовательно, к уменьшению радиуса цилиндра. Записывая 2-ой закон Ньютона для движения системы как целого вдоль радиуса, имеем

,

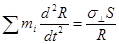(11)

где 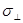 - напряжение в поперечном относительно растяжения направлении,  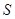- площадь системы. Учитывая, что ширина ячейки моделирования 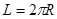, имеем для неё уравнение

,

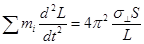(12)

Чтобы, исключить колебательные процессы, удобно ввести в правую часть уравнения слабое фиктивное затухание 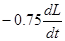. Решая уравнения для  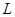на каждом временном шаге МД, мы поддерживаем ширину ячейки моделирование вблизи равновесного положения. Очевидно также, что данный подход можно использовать для демпфирования колебаний системы рассмотренных выше.

Контроль системы

Правильность работы программы МД контролировалась с помощью закона сохранения энергии:

,

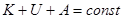(13)

где 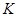 - кинетическая энергия атомов системы;  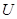- потенциальная энергия их взаимодействия; 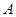- работа, произведенная над системой. Выполнение закона сохранения энергии очень важно при исследовании пластичности твердых тел. Это связано с тем, что хотя тепловое равновесие устанавливается быстро, но установление механического равновесия требует большого времени. Поэтому при деформировании система находится в тепловом равновесии, но скорее не находится в механическом равновесии, т.е. является неравновесной. Следовательно, потеря или приход энергии, вследствие невыполнения закона сохранения энергии, может существенно повлиять на характер поведения системы при деформации.

Неточное сохранение энергии связано в основном с ошибками, возникающими из-за конечного шага интегрирования по времени, а также с ошибками, возникающими из-за конечной точности представления чисел в компьютере.

Оба типа ошибок можно уменьшить, уменьшая шаг интегрирования по времени, что, однако, увеличивает время вычислений.

Другой тип ошибок возникает из-за использования потенциала с обрезанием. Скачок потенциала на радиусе обрезания при пластической деформации, когда атомы могут двигаться друг относительно друга, приводит к значительному нарушению закона сохранении энергии. Использование потенциала без скачка (3) позволяет существенно улучшить выполнения закона сохранения энергии. Потенциал (3), однако, имеет скачок производной (силы) на радиусе обрезания 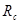. Это также приводит к несоблюдению закона сохранения энергии. Оно особенно ярко проявляется при уменьшении радиуса обрезания от канонических значений  и . 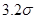Это связанно с тем, что канонические значения радиуса обрезания находятся в минимумах радиального распределения атомов гексагональной решетки. Когда же  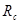попадает в максимум радиального распределения число атомов, то испытывающих действие силы (при 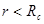), то прекращающих испытывать ее действие (при 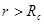), становиться очень большим, что и приводит к существенному несохранению энергии. Чтобы избавиться от скачка производной потенциала на радиусе обрезания  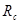потенциал был модернизирован. Пусть

,

(14)

где

(15)

и , , 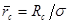. Тогда модернизированный потенциал имеет вид

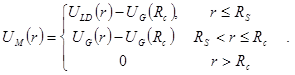
(16)

Модернизированный потенциал гладко сшивается (до второй производной) с потенциалом Леннарда-Джонса на радиусе сшивки 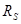 и зануляется вместе со своей первой производной на радиусе обрезания 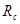. С этим потенциалом при значениях параметров  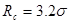и 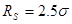 были проведены все расчеты в данной работе.