Общее количество критериев, применяемых для оценки деревообрабатывающих машин, можно разделить на две группы: общие для всех случаев (глобальные) и критерии, характерные для частных случаев [44].
Из числа глобальных наиболее важными считают следующие:
– повышение уровня автоматизации основных технологических операций;
– повышение уровня механизации и автоматизации вспомогательных операций;
– повышение непрерывности процесса обработки;
– увеличение надежности работы станка;
– снижение уровня трудозатрат живого труда в изделии;
– снижение общей трудоемкости изделия;
– повышение уровня технологичности станка;
– снижение материалоемкости (металлоемкости) станка;
– достижение оптимального расчленения станка на части;
– снижение энергопотребления;
– уменьшение габаритов станка;
– улучшение условий эксплуатации и обслуживания станка;
– повышение безопасности работы и обслуживания станка;
– улучшение внешнего вида (красоты) станка;
– повышение экологичности станка.
В качестве частных критериев, часто используемых при оценке станков и их узлов, назовем следующие:
– высокая скорость резания;
– широкий диапазон регулирования подачи;
– плавность регулирования подачи;
– точность и стабильность базирования;
– точность обработки;
– качество обработки;
– устойчивость к вибрациям;
– высокая износостойкость;
– защищенность от перегрузок;
– низкий уровень шума;
– отсутствие монотонности в работе оператора;
– легкость обслуживания;
– простота системы управления;
– отсутствие "капризных" механизмов, требующих частой наладки;
– простота и удобство наладки станка.
Для каждого конкретного случая проектирования технической системы конструктор подбирает перечень критериев развития из списка глобальных и частных критериев. Основой для выбора служат требования, предъявляемые к проектируемой системе. При этом уже на стадии выбора проектного решения конструктор стремится, чтобы система максимально удовлетворяла всем выбранным критериям.
Контрольные вопросы и задания
1. Как называют параметры технического объекта, зависимые и независимые от окружающей среды?
2. Что такое критерии развития?
3. Приведите классификацию критериев развития.
4. Как критерии развития учитывают преемственность технических объектов?
5. Поясните сущность критерия расчленения технического объекта на элементы.
6. Что учитывают эргономические критерии развития?
7. Какие критерии называют общими и частными?
Оптимизация технических решений
Общие сведения
Для решения задачи оптимизации необходимо иметь множество возможных (альтернативных) решений Y (рис. 35). В этом множестве можно выделить множество допустимых решений Y д. Решение называют допустимым, если оно удовлетворяет ограничениям (требованиям, предъявляемым к объекту): ресурсным, социальным и т.д. При этом
Y д Í Y,
где символ Í означает, что множество Yд есть часть или совпадает с множеством Y возможных решений. В множестве допустимых решений можно выделить множество эффективных решений Yэ, которое включает в себя несравнимые между собой наилучшие решения:
Yэ Í Yд.
Решение Yэ называется оптимальным, если оно обеспечивает экстремум (максимум, минимум) одновременно всех критериев. Оптимальное решение находится в множестве эффективных решений:
Yо Í Yэ.
Поскольку все критерии одновременно не могут принять экстремальные значения, то при решении многокритериальной задачи находят только рациональное решение.
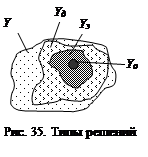 Таким образом, задача оптимизации направлена на определение наилучшего (рационального) решения, путем последовательного сужения множеств Y, Yд, Y э в соответствии с допустимыми ограничениями и принятыми критериями [45, 46]:
Таким образом, задача оптимизации направлена на определение наилучшего (рационального) решения, путем последовательного сужения множеств Y, Yд, Y э в соответствии с допустимыми ограничениями и принятыми критериями [45, 46]:
Y о Í Y э Í Y д Í Y.
Чем больше подобрано альтернативных вариантов, и чем более удачно подобраны критерии, тем больше вероятность того, что найденное решение будет самым лучшим.
В инженерной практике оптимизации можно отметить два правила:
– получение желаемого эффекта при минимуме затрат;
– получение максимального эффекта при использовании заданных ограниченных ресурсов.
Эти правила обрели значение экономических законов.
Субъектом всякого решения является лицо, принимающее решение (ЛПР). Это собирательное понятие, включающее как одно индивидуальное лицо, так и группу лиц (групповое ЛПР) [47].
ЛРП осуществляет выбор решения. Выбор – это ключевая процедура процесса оптимизации. Выбор может быть критериальный, волевой и случайный.
С помощью критериев решаются одно- и многокритериальные задачи. Выбор с помощью критериев – самый точный.
Волевой выбор решения представляет собой осознанный и ответственный выбор в условиях, когда отсутствует полный комплекс критериев.
Случайный выбор применяется при полном незнании критериев оценки. Им можно пользоваться, когда область допустимых решений минимальна.
Концепция принятия решений
Концепция принятия решений представляет собою систему взглядов, которая определяет общую направленность и методику принятия решений. Концепция включает следующие пункты [47].
1. В задаче принятия решений ЛПР выполняет основную роль. Оно принимает решения на основе своих предпочтений и несет за них ответственность.
2. Эксперты выполняют вспомогательную роль. Они несут ответственность только за свои рекомендации.
3. Измерение качества решений осуществляется на основе формирования альтернативных вариантов и их сравнительной оценки. Для оценки нужны альтернативные варианты, хотя бы два. Сравнительная оценка решений является единственным способом измерения предпочтительности в условиях отсутствия эталонов.
4. В условиях неопределенности может не существовать единственного оптимального решения. Для ЛПР, имеющих различные предпочтения, решения будут разными.
Ранжирование
Для облегчения процесса выбора, исследуемые варианты оцениваются количественно и качественно. Количественное измерение важности и предпочтительности вариантов решений выполняется методом ранжирования.
Ранжирование – это процедура упорядочения. Выполняется она ЛПР. При ранжировании варианты решений расставляются в порядке предпочтения по отношению к каждому критерию.
Если среди вариантов нет эквивалентных (равнозначных) решений, то из них можно составить последовательность
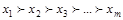 , (37)
, (37)
где вариант х1 более предпочтителен из всех вариантов;
вариант х2 менее предпочтителен х1, но предпочтительнее всех остальных и т.д.
Отношение (1) можно записать отношением чисел
с1 > с2 > с3 >… > сm.
Возможна обратная последовательность чисел
с1 < с2 < с3 <… < сm. (38)
Если наиболее предпочтительному варианту присвоить число 1, то получим числовую последовательность
1 < 2 < 3 <…< m. (39)
Здесь числа 1, 2, 3,…m называют рангами.
При ранжировании наиболее предпочтительному варианту присваивается ранг, равный единице, второму по предпочтительности – ранг, равный двум и т.д. Для эквивалентных вариантов назначаются одинаковые ранги, равные среднему арифметическому значению рангов. В этом случае, например, ранги r1 = r2 = r3 = (3+4+5)/3 = 4.
Выбор эффективных решений
Выбор решений – это заключительный и наиболее ответственный этап процесса принятия решений. Выбор выполняют путем последовательного сужения области решений и уменьшения неопределенностей. При этом множество допустимых вариантов решений сужается до множества эффективных вариантов решений. Процедура эта выполняется следующим образом.
Пусть множество допустимых решений содержит варианты Y1, Y2,… Y8. Для оценки вариантов подобраны критерии вариантов А1, А2,… А6.
Для определения эффективных решений значения всех критериев развития по вариантам приводят к рангам, и результаты заносят в таблицу (табл. 21).
Таблица 21
Ранжирование вариантов решений по критериям
| Решения | Критерии развития | |||||
| А1 | А2 | А3 | А4 | А5 | А6 | |
| Y1 | 1 | 2 | 1 | 1 | 1 | 1 |
| Y2 | 2 | 3 | 2 | 2 | 2 | 1 |
| Y3 | 3 | 1 | 3 | 3 | 3 | 3 |
| Y4 | 4 | 1 | 4 | 4 | 4 | 3 |
| Y5 | 2 | 2 | 2 | 2 | 3 | 2 |
| Y6 | 3 | 3 | 3 | 3 | 4 | 2 |
| Y7 | 4 | 1 | 4 | 4 | 5 | 4 |
| Y8 | 5 | 1 | 5 | 5 | 6 | 4 |
Сначала ранжируют варианты решений по критерию А1. Для этого надо определить: в каком решении критерий А1 наилучшим образом реализован. В приведенном примере предпочтение отдано варианту Y1, и ему присвоен ранг 1. Остальные варианты решений менее предпочтительны, и им присвоены ранги в пределах 2…5. Затем решения ранжируют последовательно по остальным критериям.
Определение области эффективных решений делается путем попарного сравнения вариантов решений. Сравнение выполняются по принципу Парето, согласно которому одно решение Yi предпочтительнее другого решения Y j, если выполняется векторное отношение “не хуже”:
(уi1, уi2, … уiq,) ³ (уj1, уj2, … уjq,).
Таким образом, одно решение предпочтительнее другого, если все значения рангов первого решения не хуже значений соответствующих рангов второго решения и, по крайней мере, для одного критерия имеет место строгое предпочтение.
Будем сравнивать решения попарно. Сравниваем ранги решений Y1 и Y2. Первое решение будет предпочтительнее второго, так как его ранги выше, а шестой ранг не хуже чем у второго. Второе решение исключается из дальнейшего рассмотрения.
Затем сравниваем Y1 и Y3. Все ранги первого решения выше, чем у третьего, но второй ранг хуже и поэтому третье решение исключить из рассмотрения нельзя.
Сравнивая попарно остальные решения, приходим к выводу, что все они хуже, чем решения Y1 и Y3. Все они исключаются из дальнейшего рассмотрения.
Таким образом, область допустимых решений сужена до двух эффективных решений Y1 и Y3.
Дата: 2019-05-29, просмотров: 266.