Разделение веществ на полярные и неполярные. Полярные имеют заряд и не могут пройти ч/з молекулу, в отличие от полярных. Следовательно, через мембрану могут легко диффундировать, жирные кислоты, различные эфиры, и др. малополярные соединения. В данном случае размеры не имеют большого значения, в отличие от полярных молекул. Так у низкомолекулярных неэлектролитов скорость мембранного переноса обратно пропорциональна квадратному корню, а у высокомолекулярных – кубическому корню из мол-ой массы. D/μ^1/2= const; D/μ^1/3=const. Частицы могут перемещаться скачками – гипотеза кинков. Кинки – лабильные (временно сущ-ие) и непрерывно перемещающиеся стр-ые полости в углеводородной части мембраны.

Движущими силами пассивного транспорта являются следующие градиенты:

- концентрационный – для нейтральных молекул.

- электрохимический – для ионов.

- осмотический – для воды.

- парциальных давлений – для газов.

При пассивном транспорте веществ, который осуществляется по градиенту концентраций, как правило, одновременно имеется несколько градиентов, которые накладываются друг на друга. В таком случае перенос веществ будет определяться результирующей всех градиентов. Если градиенты имеют одинаковые направления, то результирующий перенос будет равен сумме потоков вещества по отдельным градиентам. В случае двух противоположно направленных градиентов результирующий перенос будет равен разности потоков по отдельным градиентам.

Прохождение многих незаряженных веществ через мембраны подчиняется законам диффузии. Процесс диффузии был впервые описан Фиком:

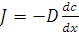, (1)

Где J – поток вещества в направлении оси х пропорционален движущей силе, т.е. градиенту концентрации dc/dx; D – коэффициент диффузии, имеет отрицательный знак, т.к. движение по градиенту, но оно идет от большего к меньшему, следовательно, реальное уменьшение кол-ва в-ва. Коэффициент диффузии зависит от размера молекулы.

Уравнение диффузии представляет частный случай более общего электродиффузионного уравнения Нернста – Планка при условии, что транспортируемые частицы не заряжены:

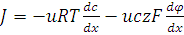, (2)

Где z – валентность иона, Т – абсолютная температура, R – газовая постоянная, F – число Фарадея.

Из сопоставления (1) и (2) видно, что:

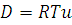, (3)

Где u – подвижность вещества в рассматриваемой среде.

В случае стационарной диффузии через тонкие мембраны dc/dx=const. Если на краях мембраны толщиной h поддерживаются постоянные концентрации вещества (с^m₁ и c^m₂), связанные с концентрациями в омываемых растворах (с₁ и с₂) соотношеними с^m₁=gc₁ и с^m₂=gc₂, где g - коэффициент распределения, то поток равен:

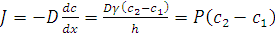, где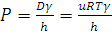

Здесь Р – проницаемость мембраны для данного вещества, коэффициент g отражает липофильность вещества.