3.2.1 Откладываем межосевое расстояние а_W=O₁O₂ – сумму радиусов начальных окружностей.

3.2.2 Проводим радиусы выступов (r_a1, r_a2), ножек (r_f1, r_f2), основных (r_b1, r_b2) и делительных (r₁, r₂) окружностей.

3.2.3 Проверяем радиальный зазор с=с*´m, где с*=0,25.

3.2.4 Проводим радиусы основных окружностей и отмечаем на них точки N₁ и N₂, O₁N₁ расположится под углом к O₁O₂ - a_Wt=25° 04'01", O₂N₂ - a_Wt=25° 04'01".

3.2.5 Через точки N₁ и N₂ проводим общую касательную к окружностям r_b1 и r_b2. N₁N₂ – есть теоретическая линия зацепления.

3.2.6 Расстояние N₁Р по теоретической линии зацепления N₁N₂ делим на 4 равные части. Такие же отрезки откладываем за точку N₁ и получаем точки 1-6.

3.2.7 Из точки 3 раствором циркуля "3-Р" делаем на r_b1 засечку – точка q. Дугу основной окружности r_b1 – qN₁ делим на 4 равные части и продолжаем деления за точку N₁, получаем точки 1,2,3,4,5.

3.2.8 Точки на основной окружности соединяем с центром вращения шестерни.

3.2.9 Перпендикулярно радиусам проводим касательные к основной окружности в каждой точке.

3.2.10 Замеряем расстояние по теоретической линии зацепления: 1Р, 2Р, …, 6Р и из точек 1', 2', …, 6' делаем засечки на соответствующих касательных.

3.2.11 Соединяем полученные точки на касательных, получаем эвольвенту 1^-го колеса.

3.2.12 Строим ножку зуба. Для этого точку q соединяем с центром вращения 1^-го колеса и радиусом r_f=0,38´m делаем скругления.

3.2.13 Отложив толщину зуба по дуге делительной окружности S₁, строим левый профиль зуба. Разделив толщину зуба пополам, получаем ось симметрии зуба.

3.2.14 Отложив шаги Р_t на хорде делительной окружности влево и вправо, получаем оси 2^-го и 3^-го зубьев и строим три зуба второго колеса.

3.2.15 Определяем длины активной линии зацепления АВ. Расстояния по теоретической линии зацепления N₁N₂ между точками пересечения окружностей выступов каждого колеса с теоретической линией зацепления – есть практическая линия зацепления.

3.2.16 Определяем дуги зацепления. Через точки теоретической линией зацепления Н₁ и Н₂ проводим правый профиль зуба первого колеса и левый профиль второго колеса.

3.2.17 Определяем рабочие части боковых профилей зубьев. Радиусами О₁Н₂ иО₂Н₁ проводим дуги до пересечения с боковыми профилями зубьев.

3.3 Синтез планетарного редуктора.

3.3.1 Выбор числа зубьев методом обращения движения.

Þ

принимаем z₄=40, тогда z₆=2,8´40=112>85 – целое число. Число z₅ определяем из условия соседства: 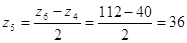>17 – целое число.

3.3.2 Проверка условия сборки.

Приняв z₄=40, z₅=36, z₆=112, проверяем передачу на условие сборки без натягов (при k=4; p=0):

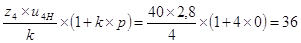– целое число, условие соблюдается.

3.3.3. Определение размеров планетарного редуктора.

, откуда

d₄=m´z₄=8´40=320 мм

d₅=m´z₅=8´36=288 мм

d₆=m´z₆=8´112=896 мм

3.3.4 Графическое построение редуктора, планов линейных и угловых скоростей.

Вычерчиваем полученный механизм в масштабе m_l=0,0064 м/мм и на вертикальную прямую сносим все характерные точки.

w₄=w₁=209,44 рад/с., тогда v_А=w₁´r₄=209,44´0,16=33,51 м/с. Строим картину линейных скоростей с масштабным коэффициентом m_v=v_А/l_vА=33,51 (м/с)/44 (мм)=0,7616 м/с/мм. Определяем скорости точек по картине линейных скоростей:

v_C=0

v_O=0

v_B=l_vВ´m_v=32 (мм)´ 0,7616 (м/с/мм)= 24,37 м/с.

Для построения плана угловых скоростей откладываем отрезок ОО и из нижнего его конца проводим лучи, параллельные картинам скоростей звеньев. Угловые скорости изображены с масштабным коэффициентом 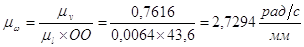, а

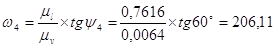рад/с, по построению - w₄= l_w4´m_w=75´2,7294=204,71 рад/с;

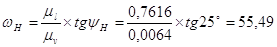рад/с, по построению - w₄= l_w4´m_w=20´2,7294=54,59 рад/с;

рад/с, по построению - w₄= l_w4´m_w=75´2,7294=119 рад/с;