Исследование механизмов методом диаграмм производится с целями:
1. Получения наглядного представления о законе движения интересующей нас точки или звена механизма.
2. Определения скоростей и ускорений точек или звеньев на основе известного закона перемещений точек или звеньев.
В курсовом проекте выполним кинематическое исследование методом диаграмм для точек D и С.
Для построения диаграммы перемещений отложим для каждого положения соответствующее перемещения ползунов D и С в масштабе mS.
Кинематические диаграммы скоростей и ускорений строим методом хорд.
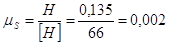
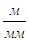 ,
,
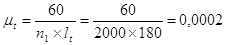
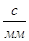
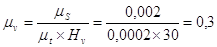

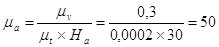
 .
.
Скорости и ускорения т. В, найденные методом диаграмм, занесём в таблицу 2.
Таблица 2
| Параметр | Значения в положениях | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| Скорость т. В, м/с | 0 | 6,9 | 10,2 | 10,2 | 6,3 | 4,8 | 0 | 4,5 | 7,5 | 9,6 | 10,2 | 6,3 |
| Ускорение т. В, м/с2 | 2600 | 1650 | 600 | 450 | 1000 | 1350 | 1400 | 1325 | 1000 | 450 | 600 | 1650 |
Определение приведённых моментов сил.
Мпр – расчётный момент пары сил, определяемый из равенства его элементарной работы, равен сумме элементарных работ сил и моментов пар сил, действующих на звенья механизма.
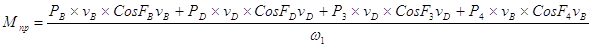 ,
,
где PB и PD определяются по индикаторной диаграмме.
Пример вычисления Мпр для положения 1:
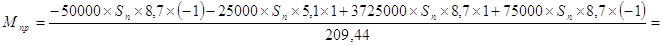 =1698,14 Н´м.
=1698,14 Н´м.
Так как сила действует по направляющей и скорость направлена параллельно направляющей, то косинус угла равен ±1, а угол равен 0° или 180° в зависимости от положения механизма.
Или иначе:
 , где
, где 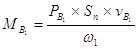 , где
, где  = 3,14´0,0036»0,011 м2 – площадь поверхности поршня.
= 3,14´0,0036»0,011 м2 – площадь поверхности поршня.
Результаты измерений и вычислений занесём в таблицу 3.
Таблица 3
| угол, ° | PВ, Па | МВ, Н´м | Мпр, Н´м | vB, м/с |
| 1 | 2 | 3 | 4 | 5 |
| 0 | 50000 | 0,00 | 0,00 | 0,00 |
| 30 | -50000 | 22,85 | 1 698,14 | 8,70 |
| 60 | -50000 | 37,03 | 1 336,53 | 14,10 |
| 90 | -50000 | 37,03 | 703,52 | 14,10 |
| 120 | -50000 | 27,57 | 170,96 | 10,50 |
| 150 | -50000 | 13,39 | -249,54 | 5,10 |
| 180 | -50000 | 0,00 | 0,00 | 0,00 |
| 210 | -25000 | -6,70 | 1 698,14 | 5,10 |
| 240 | 12500 | -6,70 | 1 336,53 | 10,20 |
| 270 | 100000 | -74,05 | 703,52 | 14,10 |
| 300 | 300000 | -219,80 | 170,96 | 13,95 |
| 330 | 862500 | -394,10 | -249,54 | 8,70 |
| 360 | 1450000 | 0,00 | 0,00 | 0,00 |
| 390 | 3725000 | 1702,07 | 1 698,14 | 8,70 |
| 420 | 1800000 | 1332,98 | 1 336,53 | 14,10 |
| 450 | 1050000 | 777,57 | 703,52 | 14,10 |
| 480 | 725000 | 399,82 | 170,96 | 10,50 |
| 510 | 575000 | 154,02 | -249,54 | 5,10 |
| 540 | 250000 | 0,00 | 0,00 | 0,00 |
| 570 | 75000 | -20,09 | 1 698,14 | 5,10 |
Продолжение таблицы 3
| 1 | 2 | 3 | 4 | 5 |
| 600 | 50000 | -26,79 | 1 336,53 | 10,20 |
| 660 | 50000 | -36,63 | 170,96 | 13,95 |
| 690 | 50000 | -22,85 | -249,54 | 8,70 |
| 720 | 50000 | 0,00 | 0,00 | 0,00 |
Строим диаграмму Мпр=Мпр(j) с масштабным коэффициентом 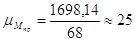
 , а
, а 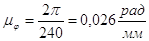 .
.
2.5.1 Определение работ сил сопротивления и движущих сил
Интегрируя диаграмму приведённых моментов сил сопротивления, получим диаграмму работы сил сопротивления с масштабным коэффициентом: 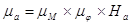
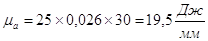 .
.
Полагая, что приведённый момент сил сопротивления имеет постоянную величину во всех положениях кривошипа, то величину Мдв. определяем на основе закона передачи работы при установившемся режиме действия механизма.
За период установившегося движения работа движущих сил равна работе сил сопротивления. При этом условии диаграмма Ас=Ас(j) работ сил сопротивления будет представлять собой наклонную прямую, соединяющую начало координат с последней точкой графика.
Продифференцировав диаграмму Ас=Ас(j), получим на диаграмме Мпр прямую, которая и является диаграммой моментов сил сопротивления.
2.5.2 Определение суммарной работы.
Вычитая из ординат график Ад=Ад(j) ординаты графика Ас=Ас(j), получим диаграмму приращения кинетической энергии машины с маховиком или диаграмму суммарной работы.
 .
.
2.5.3 Определение приведённых моментов инерции.
Приведённый моментов инерции – это такой условный момент, обладая которым звено приведения развивает кинетическую энергию, равную сумме кинетических энергий всех звеньев.
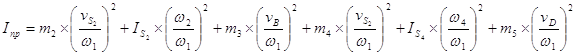 ,
,
где  кг´М2, т.о. IS2= IS4.
кг´М2, т.о. IS2= IS4.
Пример расчёта:
 = =0,0155 кг´м2.
= =0,0155 кг´м2.
Результаты и вычислений занесём в таблицу 4.
Таблица 4
| угол, ° | Iпр, кг´м2 |
| 1 | 2 |
| 0 | 0,0155 |
| 30 | 0,0251 |
| 60 | 0,0446 |
| 90 | 0,0526 |
| 120 | 0,0439 |
Продолжение таблицы 4
| 1 | 2 |
| 150 | 0,0247 |
| 180 | 0,0155 |
| 210 | 0,0252 |
| 240 | 0,0442 |
| 270 | 0,0526 |
| 300 | 0,0438 |
| 330 | 0,0252 |
| 360 | 0,0155 |
| 390 | 0,0251 |
| 420 | 0,0446 |
| 450 | 0,0526 |
| 480 | 0,0439 |
| 510 | 0,0247 |
| 540 | 0,0155 |
| 570 | 0,0252 |
| 600 | 0,0442 |
| 630 | 0,0526 |
| 660 | 0,0438 |
| 690 | 0,0252 |
| 720 | 0,0155 |
2.5.4 Построение диаграммы Т2=Т2(j)
Определим кинетическую энергию по формуле:


Найденные значения записываем в таблицу 5.
Таблица 5
| положение | Т2 |
| 1 | 2 |
| 0 | 339,81 |
| 1 | 549,73 |
| 2 | 977,93 |
| 3 | 1153,10 |
| 4 | 962,32 |
| 5 | 540,97 |
| 6 | 339,81 |
| 7 | 553,70 |
| 8 | 968,61 |
| 9 | 1153,10 |
| 10 | 960,15 |
| 11 | 553,39 |
| 12 | 339,81 |
| 13 | 549,73 |
| 14 | 977,93 |
| 15 | 1153,10 |
| 16 | 962,32 |
| 17 | 540,97 |
| 18 | 339,81 |
| 19 | 553,70 |
Продолжение таблицы 5
| 1 | 2 |
| 20 | 968,61 |
| 21 | 1153,10 |
| 22 | 960,15 |
| 23 | 553,39 |
| 24 | 339,81 |
2.5.5 Построение диаграммы изменения кинетической энергии DТ1=DТ1(j).
Строим диаграмму изменения кинетической энергии путём вычитания из кривой суммарной работы значений Т2, при этом диаграмма суммарной работы и Т2 выполнены в одном масштабе.
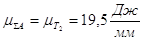 .
.
Определяем DТ1наиб. и вычисляем значение Iпр1:
 кг´м2,
кг´м2,
при этом момент инерции маховика 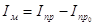 , где Iпр0 – момент инерции звена, приведения и звеньев, связанных со звеном приведения постоянством передаточного отношения.
, где Iпр0 – момент инерции звена, приведения и звеньев, связанных со звеном приведения постоянством передаточного отношения.
2.5.6 Определение размеров маховика.
Момент инерции маховика коленвала должен быть таким, чтобы колебания угловой скорости машины, заданные коэффициентом неравномерности вращения s не выходил за предел колебания угловой скорости wmax и wmin.
Если  , и Iпр0=0, то
, и Iпр0=0, то 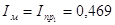 кг´м2. Масса маховика определяется по формуле:
кг´м2. Масса маховика определяется по формуле:
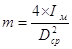 ,
,
где Dср – средний диаметр маховика принимаем равным 0,4 м, т.о. 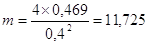 кг. Зная массу и плотность (g=7800 кг/м3), вычислим значения S и b:
кг. Зная массу и плотность (g=7800 кг/м3), вычислим значения S и b:
1). Находим объём маховика: 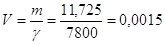 м3.
м3.
2). Определим толщину S и ширину обода b: 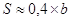 ;
; 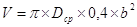 , откуда
, откуда
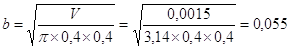 м Þ S=0,4´0,055=0,022 м.
м Þ S=0,4´0,055=0,022 м.
2.5.7 Определение закона движения ведущего звена
При принятых допущениях изменение угловой скорости Dw1 ведущего звена пропорционально изменению кинетической энергии DТ1 звеньев первой группы. В Связи с этим, диаграмма DТ1=f(j1) может являться и диаграммой угловой скорости кривошипа w1, если принять равенство соответствующих ординат.
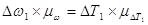 .
.
Т.к. mDТ1 уже выбран, то масштабный коэффициент mw определяется следующим образом:  .
.
Начало координат осей на диаграмме w1=f(j1) определяется ординатой  .
.
Дифференцируем диаграммуw1=f(j1) и получаем диаграмму аналога углового ускорения кривошипа ej=f(j1). При этом масштабный коэффициент вычисляется по формуле:
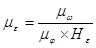 , где Нe - полюсное расстояние, Нe=30 мм.
, где Нe - полюсное расстояние, Нe=30 мм.  .
.
Для определения углового ускорения кривошипа e1 воспользуемся следующей формулой:
 .
.
Пример расчёта: ej=[ej]´me=22 мм´0,255 с-1/мм=5,61 с-1, тогда
e1=5,61´209,03=1172,648 рад/с2.
Результаты измерений и вычислений занесём в таблицу 6.
Таблица 6
| положение | Dw1 | w1 | e1 | ej |
| 0 | 1,8 | 211,20 | 0 | 0,00 |
| 1 | 0,9 | 210,35 | 1180,081 | 5,61 |
| 2 | -1,1 | 208,37 | 1328,367 | 6,38 |
| 3 | -1,8 | 207,68 | 0 | 0,00 |
| 4 | -0,4 | 209,03 | 1172,648 | 5,61 |
| 5 | 1,7 | 211,14 | 1346,011 | 6,38 |
| 6 | 1,8 | 211,20 | 0 | 0,00 |
| 7 | 0,9 | 210,31 | 1179,854 | 5,61 |
| 8 | -1,0 | 208,47 | 1328,973 | 6,38 |
| 9 | -1,8 | 207,68 | 0 | 0,00 |
| 10 | -0,4 | 209,05 | 1172,772 | 5,61 |
| 11 | 1,6 | 211,01 | 1345,203 | 6,38 |
| 12 | 1,8 | 211,20 | 0 | 0,00 |
| 13 | 0,9 | 210,35 | 1180,081 | 5,61 |
| 14 | -1,1 | 208,37 | 1328,367 | 6,38 |
| 15 | -1,8 | 207,68 | 0 | 0,00 |
| 16 | -0,4 | 209,03 | 1172,648 | 5,61 |
| 17 | 1,7 | 211,14 | 1346,011 | 6,38 |
| 18 | 1,8 | 211,20 | 0 | 0,00 |
| 19 | 0,9 | 210,31 | 1179,854 | 5,61 |
| 20 | -1,0 | 208,47 | 1328,973 | 6,38 |
| 21 | -1,8 | 207,68 | 0 | 0,00 |
| 22 | -0,4 | 209,05 | 1172,772 | 5,61 |
| 23 | 1,6 | 211,01 | 1345,203 | 6,38 |
| 24 | 1,8 | 211,20 | 0 | 0,00 |
Дата: 2019-05-29, просмотров: 281.