Гетеропереходом называется контакт двух различных по химическому составу полупроводников. Если полупроводники имеют одинаковый тип проводимости, то они образуют изотипный гетеропереход. Если тип их проводимости различен, то получается анизотипный гетеропереход.
Для получения идеальных монокристаллических гетеропереходов без дефектов решетки и поверхностных состояний на границе раздела необходимо, чтобы у полупроводников совпадали типы кристаллических решеток, их периоды и коэффициент термического расширения. Для их получения периоды решеток должны совпадать с точностью ~0,1%. Пример идеального гетероперехода: GaAS -AIGaAS [1].
Модель зоны структуры идеального резкого гетероперехода без ловушек на границе раздела была предложена Андерсеном, который использовал результаты работы Шокли [2].
На рис.1 приведена зонная диаграмма двух изолированных полупроводников, у которых различные значения ширины запрещенной зоны Еg , диэлектрической проницаемости e, работы выхода j m и электронного сродства c .
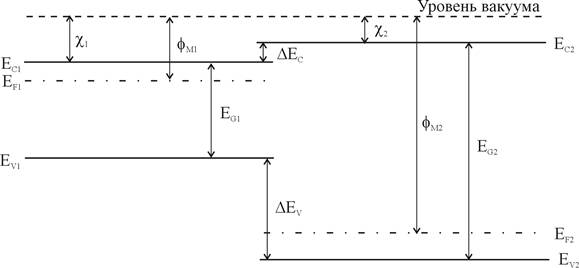
Работа выхода и электронное сродство определяются как энергия, необходимая для удаления электрона с уровня Ферми Еf и со дна зоны проводимости Еc в вакуум соответственно. Различие в положении дна зоны проводимости полупроводников обозначено D Еc; а различие в положении потолка валентной зоны ΔEv. На рисунке 1 показан случай, когда ΔЕc=(χ1-χ2).
|
| Рис. 1. Зонная диаграмма двух изолированных полупроводников при условии электронейтральности |
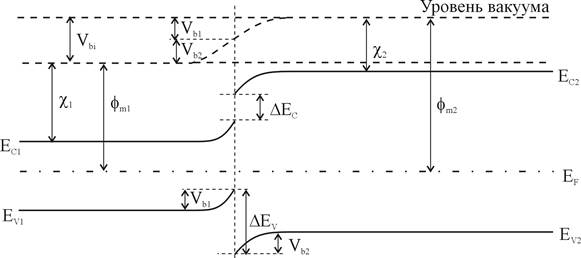
Зонная диаграмма анизотипного p-n - гетероперехода в равновесии, образованного этими полупроводниками приведена на рис.2.
|
| Рис.2. Зонная диаграмма идеального анизотипного p-n гетероперехода при тепловом равновесии. |
Положение уровня Ферми в равновесном состоянии должно быть одинаково по обе стороны перехода, а уровень энергии, соответствующий вакууму, должен быть параллелен краям зон и непрерывен. Поэтому разрыв в положении краев зоны проводимости и краев валентной зоны не связан с уровнем легирования.
Полный контактный потенциал Vbi. равен сумме потенциалов Vb1+Vb2, где Vb1 и Vb2 - электростатические потенциалы равновесия состояния первого и второго полупроводников соответственно.
Ширину обедненного слоя (W) в каждом полупроводнике и барьерную емкость (С) можно найти решив уравнение Пуассона для резкого перехода с каждой стороны границы раздела. Одним из граничных условий является непрерывность электрической индукции на границе раздела, т.е. ε1E1= ε2E2. В результате имеем:
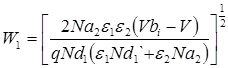
| (1) |
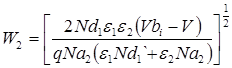
| (2) |
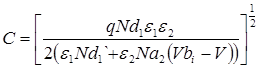
| (3) |
где Nd1 - концентрация доноров в 1-м полупроводнике;
Na2 - концентрация акцепторов во 2-м полупроводнике.
Отношение напряжений в каждом полупроводнике составляет:
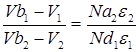
| (4) |
где V=V1+V2 - полное приложенное напряжение.
Вольт - амперная характеристика принимает вид:
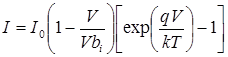
| (5) |
где I - плотность тока.
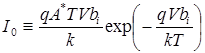
| (6) |
Приведенное выражение отличается от вольт - амперной характеристики контакта металл-полупроводник множителем I0, а также характером зависимости от температуры. Обратный ток не имеет насыщения, а при больших V линейно возрастает с напряжением. В прямом направлении зависимость I от допускает аппроксимацию экспоненциальной функцией, т.е.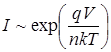 
.
Механизмы протекания тока.
В резком гетеропереходе благодаря разрывам ΔEc и ΔEv высоты потенциальных барьеров для электронов и дырок разные. Поэтому при прямом смещении в гетеропереходе обычно происходит односторонняя инжекция носителей из широкозонного полупроводника в узкозонный.
Инжектированные носители (в данном случае дырки) должны преодолеть потенциальные барьеры (“пики”), возникающие из-за разрывов зон. Механизмы протекания тока через эти барьеры, дополнительные по сравнению с p-n - переходом (туннельный и термоинжекционный) зависят от величины смещения на гетеропереходе, температуры, а также от степени легирования полупроводников.
В плавном гетеропереходе заряда на неосновные носители заряда действует внутреннее электрическое поле εi, возникающее вследствие изменения Eg. При прямом смещении в этом случае также происходит односторонняя инжекция дырок в более узкозонную часть.
Фотоэффект.
Как и в p-n переходе фотоэффект в гетеропереходе возникает за счет пространственного разделения в поле объемного заряда носителей, возбужденных светом. При освещении полупроводника со стороны широкозонного полупроводника в узкозонном поглощаются фотоны с энергией:
| Eg1<h υ<Eg2 | (7) |
где h - постоянная Планка
υ - частота излучения.
Широкозонный полупроводник служит в этом случае "окном", прозрачным для света, поглощаемого в узкозонном слое, и защищает область генерации неравновесных электронно-дырочных пар от рекомбинационных потерь на поверхности кристалла [2].
§ 2. Модели токопереноса в гетеропереходе CdS – Cu2S.
Система CdS-Сu2S представляет собой неидеальный анизотипный гетеропереход у которого различие постоянных кристаллических решеток контактирующих полупроводников CdS (5.832 Å) и Cu2S (5.601 Å) составляет 4%. Столь значительное различие периодов решеток при формировании гетероперехода создает высокую плотность дислокаций несоответствия на поверхности раздела. Оборванные связи в дислокациях приводят к появлению энергетических уровней в запрещенной зоне, ответственных за захват носителей или за их рекомбинацию и оказывают существенное влияние на перенос заряда через обедненную область [3,4].
Было предложено немало моделей, объясняющих процессы, протекающие в гетеропереходе. Вид зонной диаграммы и характер токопрохождения не могут быть описаны в рамках модели Андерсона, учитывающей только ток, текущий благодаря инжекции.
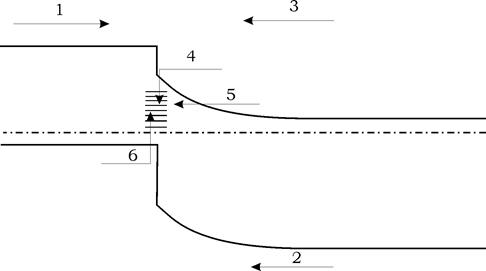
Для гетероперехода известно несколько вероятных механизмов протекания тока через область барьера, реализующихся в зависимости от внешних условий: электронный и дырочный токи при фотовозбуждении (1,2), термоэмиссионный (3), эмиссионно-рекомбинационный (4), туннельно-рекомбинационный ток (5,6) (См. рис.3) .
|
| Рис.3. Вероятные механизмы токопереноса в области пространственного заряда гетероперехода CdS-Cu2S. |
Для согласования теории с данными экспериментов, Бьюб предложил модель туннелирования электронов через "зубец" в зоне проводимости. Ширина "зубца", а следовательно и вклад туннельного тока в вольтамперную характеристику определялась глубокими уровнями дефектов в ОПЗ. Однако этот случай реализуется далеко не всегда.
Модель многоступенчатого туннелирования через эти состояния с последующей рекомбинацией на гетерограницах предложили Райбен и Фойхт для Ge-GaAs и Мартинуцци для CdS-Cu2S. При таком подходе, однако, невозможно точно определить вероятность туннельных переходов с одного уровня на другой и не учитывается ограничение туннельной проводимости скоростью рекомбинационных процессов на границе раздела.
В ряде публикаций [5,6,7,8] был предложен туннельно-прыжковый механизм токопереноса. Здесь учтены статистические распределения носителей и их взаимодействие с фононами. Определена также вероятность "прыжка" между соседними локальными состояниями.
Большое количество моделей, объясняющих процессы в гетеропереходах CdS-Cu2S, обусловлено различной технологией их получения, нестабильностью гетеропереходов в процессе работы, деградацией характеристик и другими причинами [3].
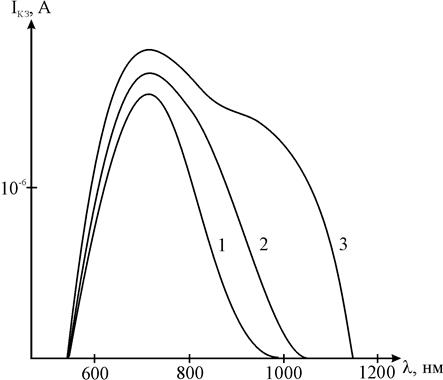
На рисунке 4 приведены типичные кривые спектрального распределения тока короткого замыкания гетеропереходов с различным химическим составом базового слоя. [3].
|
| Рис.4. Спектральное распределение тока короткого замыкания тыльнобарьерных фотоэлементов с различным составом базового слоя: |
| 1 - нелегированный CdS; |
| 2 - CdS с примесью 0.01% In; |
| 3 - CdZnS с примесью 0.2% In. |
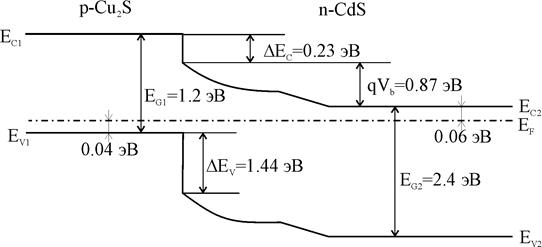
На рисунке 5 изображена детальная зонная диаграмма гетераперехода, построенная Дасом, который использовал теоретическую модель Ротворфа и другие модели. Значения всех параметров перехода, использованные в этой диаграмме, были определены экспериментально [4].
|
| Рис.5. Энергетическая зонная диаграмма гетероперехода CdS-Cu2S. |
Фотоэлектрические свойства гетероперехода CdS-Cu2S подробно рассмотрены ниже.
§ 3. Фотоэлектрические свойства гетероперехода CdS-Cu2S.
В основу формирователя сигналов изображения положено свойство неидеального гетероперехода CdS-Cu2S накапливать положительный заряд неравновесных дырок на локальных уровнях.
На зонной диаграмме (рис.6) изображены процессы, происходящие в ФСИ при освещении.
Резкое различие в проводимости сульфидов кадмия и меди приводит к тому, что область пространственного заряда локализована практически полностью со стороны CdS [4].
|
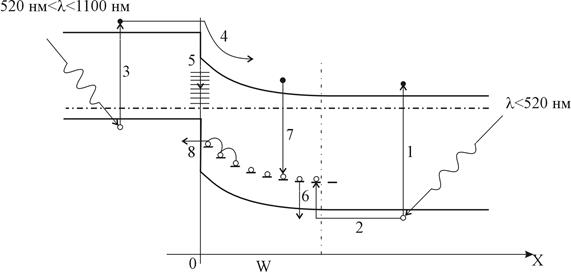
| Рис.6. Зонная диаграмма ФСИ. |
При фотовозбуждении квантами из области собственного поглощения сульфида кадмия появляются неравновесные электроны и дырки (переходы 1). Электроны удаляются полем барьера в объем базовой области, а дырки захватываются вблизи границы раздела на ловушки и центры рекомбинации (переходы 2). Наличие таких компенсирующих центров с большой концентрацией фактически является одним из основных свойств рассматриваемого гетероперехода. Поле барьера способствует накоплению дырок в ОПЗ, поэтому даже при незначительном уровне фотовозбуждения распределение положительного заряда в CdS значительно изменяется, что приводит к росту емкости перехода. Кроме того, распределение энергии электрона от координаты изменяется с квадратичного на экспоненциальное. При этом резко возрастает напряженность электрического поля у границы раздела гетероперехода [3].
Ток короткого замыкания Iкз формирователя изображения находится в прямой зависимости от пространственного распределения электрического потенциала φ(x), а это распределение непосредственно связано с концентрацией дырок, локализованных на ловушках.
Как показано в [3]:
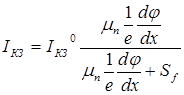
| (8) |
где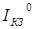 
- фототок в отсутствие потерь на границе раздела;
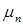- подвижность электронов в CdS;
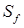- скорость поверхностной рекомбинации на границе раздела.
Поскольку дрейфовая скорость электронов определяется из соотношения:
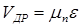
| (9) |
что равнозначно:
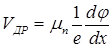
| (10) |
выражение (8) можно переписать:
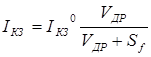
| (11) |
Таким образом, изменяя освещенность гетероперехода с помощью собственной для сульфида кадмия подсветки можно управлять распределением φ(x), а, следовательно, и дрейфовой скоростью электронов и величиной тока короткого замыкания Iкз.
При проецировании на образец какого-либо изображения, его точки освещаются по разному, что приводит к различной концентрации дырок, захваченных на ловушки и соответственно к различному изгибу энергетических зон в ОПЗ.
Если проецирование прекратить, то различие в концентрации дырок сохраняется достаточно долгое время что позволяет использовать гетеропереход в качестве устройства, запоминающего оптическую информацию.
Считывание этой информации возможно при сканировании образца инфракрасным светом. Длительность ИК - импульсов при сканировании должна быть как порядка 10 мкс, так как более длинные импульсы будут вызывать активное оптическое опустошение ловушек, т.е. высвобождение дырок с локальных уровней в валентную зону (переход 6).
С помощью ИК - подсветки можно также производить стирание изображения, при этом образец освещают импульсами большой длительности с высокой частотой следования. После чего образец пригоден для повторного запоминания другого изображения.
Информация, полученная при сканировании образца, обрабатывается компьютерными методами и затем может воспроизводиться на экране компьютера. Процессы записи и считывания могут быть значительно разнесены во времени, однако длительное хранение сопровождается термическим опустошением ловушек, что приводит к постепенной утрате оптической информации.
При хранении образца при температуре около 0oС считывание информации возможно в течении 6-8 дней. Повышение температуры хранения приводит к более быстрому термическому высвобождению дырок в валентную зону.
Более подробно явления удаления захваченного заряда будут рассмотрены ниже.
§ 4. Механизмы выброса захваченного заряда в ОПЗ гетероперехода CdS-Cu2S.
Гетеропереход CdS-Cu2S может находиться в двух различных состояниях. Одно из них - равновесное - обладает низкой чувствительностью к инфракрасному свету и позволяет получить невысокое значение тока Iкз. Другое состояние - неравновесное - высокочувствительно к ИК - свету и дает значительно большую величину тока короткого замыкания.
Переход из равновесного состояния в неравновесное осуществляется при действии коротковолнового света за счет описанного выше эффекта захвата и накопления неравновесных дырок на ловушках в ОПЗ CdS
Время сохранения структурой неравновесного состояния определяется величиной рекомбинационного барьера и процессом выброса дырок из ловушек, идущего наряду с накоплением. Но после прекращения действия коротковолновой подсветки выброс начинает играть решающую роль в токопереносе, так как освобождение захваченного заряда обусловливает обратные изменения параметров барьера и переход структуры из неравновесного состояния в равновесное.
Интенсивность выброса определяет величину и скорость этого изменения параметров барьера, а значит и Iкз. Поэтому представляется важным звать, как именно выброс влияет на параметре барьера после прекращения фотовозбуждения коротковолновым светом, как быстро они изменяются со временем.
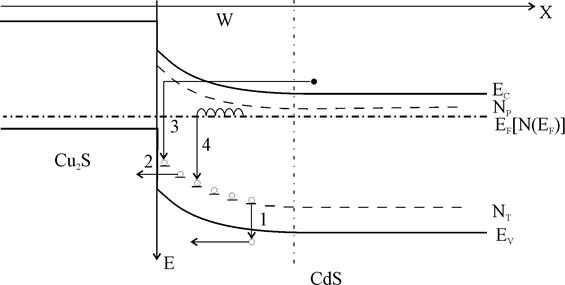
Удаление дырок, захваченных на ловушки в ОПЗ CdS, возможно по следующим четырем механизмам (Рис.7):
1.термический выброс в валентную зону CdS (переход 1);
2.непосредственное туннелирование дырок с ловушечных центров валентную зону Cu2S (переход 2);
3.двухступенчатое туннелирование электрона из квазинейтральной области CdS в ОПЗ (переход 3) и последующей рекомбинации с неравновесной дыркой;
4.туннельно-прыжковая рекомбинация (переход 4)
|
| Рис.7. Механизмы удаления захваченных на ловушки дырок из ОПЗ гетероперехода CdS-Cu2S |
Наличие последнего механизма связано с тем, что дефекты трансляционной симметрии в ОПЗ приводят к размыванию краев разрешенных зов и образованию в запрещенной зоне отличной от нуля плотности состояний N(E). По этим локальным состояниям возможен токоперенос, описываемый с позиций модели прыжковой проводимости Мотта. Часть электронов, находящихся на локализованных состояниях, может рекомбинировать с дырками, захваченными на ловушки, очевидно, что рекомбинировать могут лишь носители, находящиеся вблизи уровня Ферми, т.к. выше носителей нет. а ниже все состояния заполнены и прыжок совершить некуда. Таким образом, рекомбинировать могут только относительно подвижные носители, расположенные на энергетическом расстоянии порядка kT от уровня Ферми EF.
Вероятности осуществления указанных механизмов находятся в сильной зависимости от глубины залегания дырочных ловушек, ET, температуры образца и пространственной координаты локальных центров в ОПЗ.
Внешнее смещение оказывает на механизёмы выброса разное влияние, так, термический выброс (1) от напряжения не зависит вообще, непосредственное туннелирование (2) зависит слабо, а двухступенчатая рекомбинация я туннельно-прыжковый механизм проявляют сильную зависимость от внешнего смещения.
Кинетика выброса дырок по перечисленным механизмам при фотовозбуждении описывается уравнением:
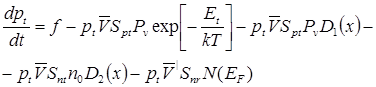
| (12) |
где f -функция генерации, имеющая постоянное значение;
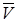-тепловая скорость носителей;
Spt и Snt-поперечное сечение захвата дырок я электронов
Pv-эффективная плотность состояний в валентной зоне CdS;
n0-концентрация свободных электронов в квазинейтральной области CdS;
Snr-поперечное сечение захвата электронов центром рекомбинации на границе раздела;
- N(EF) -плотность состояний в окрестности уровня Ферми;
-D1(х),D2(х)-коэффициенты прозрачности барьеров, соответствующих туннелированию я двухступенчатой рекомбинации;
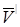-эффективная тепловая скорость носителей при прыжковой проводимости.
Второе слагаемое в правой части описывает термический выброс (1), третье - туннельный (2), четвертое - двухступенчатое туннелирование (3), а пятое – туннельно-прыжковую рекомбинацию (4).
Рассмотрим кинетику выброса дырок в отсутствии фотовозбуждения, то есть случай спадающей релаксации. Пусть при t=0 (в момент выключения коротковолнового света) концентрация на ловушках такова, что условие:
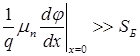
| (13) |
выполняется. В этом случае рекомбинационными потерями на границе можно пренебречь и ток, генерированный длинноволновым светом в Cu2S, будет максимален. После выключения света при t=0 в уравнении (12) функция генерации f оказывается равной нулю. В то же время начальное условие записывается в виде
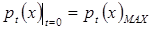
| (14) |
Безусловно, при всех значениях x pt(x)≤Nt. Таким образом, уравнение (12) перепишется в виде:
 
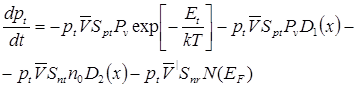
| (15) |
Данное уравнение определяет зависимость концентрации носителей захваченных на дырочные ловушки в ОПЗ гетероперехода CdS-Cu2S от времени, прошедшего после выключения возбуждающего света.
Решение кинетического уравнения для неравновесных дырок с концентрацией pt, захваченных не ловушки в ОПЗ CdS, учитывающего все пути ликвидации накопленного заряда, определяет процесс спада тока короткого замыкания, т.к. кинетика находится в прямой зависимости от кинетики захваченного заряда.
§ 5. Технология изготовления гетеропары CdS-Cu2S.
Дата: 2019-05-29, просмотров: 357.
