Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Далее, пусть многоугольник составлен из нескольких многоугольников так, что внутренние области любых двух из этих многоугольников не имеют общих точек. Очевидно, величина части плоскости, занимаемой всем многоугольником, является суммой величин тех частей плоскости, которые занимают составляющие его многоугольники. Итак:

Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

Свойства 1⁰ и 2⁰ называют основными свойствами площадей. Аналогичными свойствами обладают и длины отрезков.

Наряду с этими свойствами нам понадобится еще одно свойство площадей.

Площадь квадрата равна квадрату его стороны

Краткую формулировку этого свойства следует понимать так: если сторона квадрата при выбранной единице измерения отрезков выражается числом а, то площадь этого квадрата выражается числом а².

Площадь квадрата

Докажем, что площадь S квадрата со стороной а равна а².

Начнем с того, что а = , где n – целое число. Возьмем квадрат со стороной 1 и разобьем его на n² равных квадратов так, как показано на рисунке а) (на рисунке n=5).

 

рис. а)

 

a= 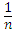Так как площадь большого квадрата равна 1, то площадь каждого маленького квадрата равна 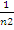^. Сторона каждого маленького квадрата равна , т.е. равна а. Итак,

 

S= 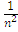=  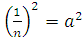     (формула 1)

 

Пусть теперь число а представляет собой конечную десятичную дробь, содержащую n знаков после запятой (В частности, число а может быть целым, и тогда n=0). Тогда число m= 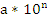 целое. Разобьем данный квадрат со стороной а на m² равных квадратов так, как показано на рисунке б) (на рисунке m=7)

 

рис. б)

 

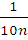При этом каждая сторона данного квадрата разобьется на m равных частей и, значит, сторона любого маленького квадрата равна

 

 

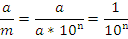
По формуле 1 площадь маленького квадрата равна 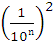. Следовательно, площадь S данного квадрата равна

 

 

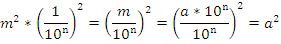
Наконец, пусть число а представляет собой бесконечную десятичную дробь. Рассмотрим число а, получаемое из а отбрасыванием всех десятичных знаков после запятой, начиная с (n+1) – го. Так как число а отличается от а _n не более чем на 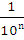, то 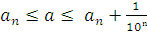, откуда

 

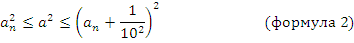
Ясно, что площадь S данного квадрата заключена между площадью квадрата со стороной 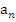 и площадью квадрата со стороной  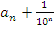(рисунок в)), т.е. между  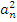и :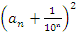

 

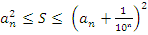 (формула 3)

 

рис. в)

 

 

 

 

 

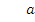
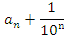
Будем неограниченно увеличивать число n. Тогда число 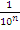 будет становиться сколь угодно малым, и, значит, число  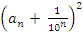будет сколь угодно мало отличаться от числа 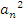. Поэтому из неравенств (2) и (3) следует, что число S сколь угодно мало отличается от числа 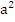. Следовательно, эти числа равны: 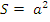, что и требовалось доказать.

 

Площадь прямоугольника

Теорема:

Площадь прямоугольника равна произведению его смежных сторон

Доказательство:

Рассмотрим прямоугольник со сторонами a, b и площадью S (рис. а). Докажем,

что S = ab.

 

Рис. а)

b

a

 

Достроим прямоугольник до квадрата со стороной a + b, как показано на (рис. б)

По свойству 3⁰ площадь этого квадрата равна .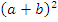

 

Рис. б)

a2

a b

 

a a

 

b b

a b

 

С другой стороны, этот квадрат составлен из данного прямоугольника с

площадью S, равного ему прямоугольника с площадью S (свойство 1⁰ площадей) и двух квадратов с площадями a² и b² (свойство 3⁰ площадей). По свойству 2⁰ имеем:

 

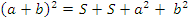, или .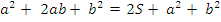

 

Отсюда получаем: S = ab. Теорема доказана.

Площадь параллелограмма

Основание – одна из сторон параллелограмма

Высота параллелограмма – перпендикуляр, проведенный из любой точки

Противоположной стороны к прямой, содержащей основание.

Теорема

Площадь параллелограмма равна произведению его основания на высоту.

Доказательство:

Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD

за основание и проведем высоты BH и CK (см. рис.). Докажем, что S = AD 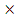BH.

Докажем сначала, что площадь прямоугольника HBCK также равна S.

Трапеция ABCK составлена из параллелограмма ABCD и треугольника ABH.

Но прямоугольные треугольники DCK и ABH равны по гипотенузе и острому углу (их гипотенузы AB и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых AB и CD секущей AD), поэтому их площади равны.

Следовательно, площади параллелограмма ABCD и прямоугольника HBCK также равны, т.е. площадь прямоугольника HBCK равна S. По теореме о площади прямоугольника S = BC  BH, а так как BC = AD, то S = AD  BH. Теорема доказана.

 

B C

 

A H D K

 

Площадь треугольника

Теорема

Площадь треугольника равна половине произведения его основания на высоту.

Доказательство:

Пусть S – площадь треугольника ABC (см. рис.). Примем сторону AB за основание треугольника и проведем высоту CH. Докажем, что 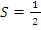 AB  CH.

Достроим треугольник ABC до параллелограмма ABCD так, как показано на рисунке. Треугольники ABC и DCB равны по трем сторонам (BC – их общая сторона, AB = CD и AC = BD как противоположные стороны параллелограмма ABDC), поэтому их площади равны. Следовательно, площадь S треугольника ABC равна половине площади параллелограмма ABDC, т.е. 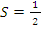 AB  CH. Теорема доказана.

 

C D

 

 

A H B

Следствие 1