Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

 

Курсовая работа

 

1054 02 0623 000 РР

 

 

 

	Должность	Фамилия И. О.	Подпись	Дата
Выполнил	Студент	Иванов И.И.
Проверил	Доцент	Петров А.П.
Принял

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

ЗАДАНИЕ. На вал установлены два колеса диаметрами D₁ и D₂ , нагруженные силами от сопряженных колес (Схема № 6, рис. 1).

Необходимо:

    – подобрать диаметр вала d из условия статической прочности. В опасном сечении вала построить эпюры нормальных и касательных напряжений и показать напряженное состояние тела в опасной точке;

– произвести расчет вала на жесткость по линейным перемещениям в местах установки колес и по угловым перемещениям в опорах. Уточнить диаметр вала;

– выполнить проверочный расчет вала на усталостную прочность в двух опасных сечениях.

Исходные данные для расчета. Вариант № 2-3.

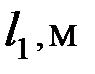
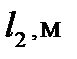
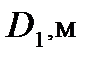
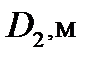
Вар. №	N1,кН	R1,кН	P1,кН	Вар. №						Материал
2	0,82	0,47	2,6	3	0,2	0,4	0,1	0,3	0,2	15ХС

 

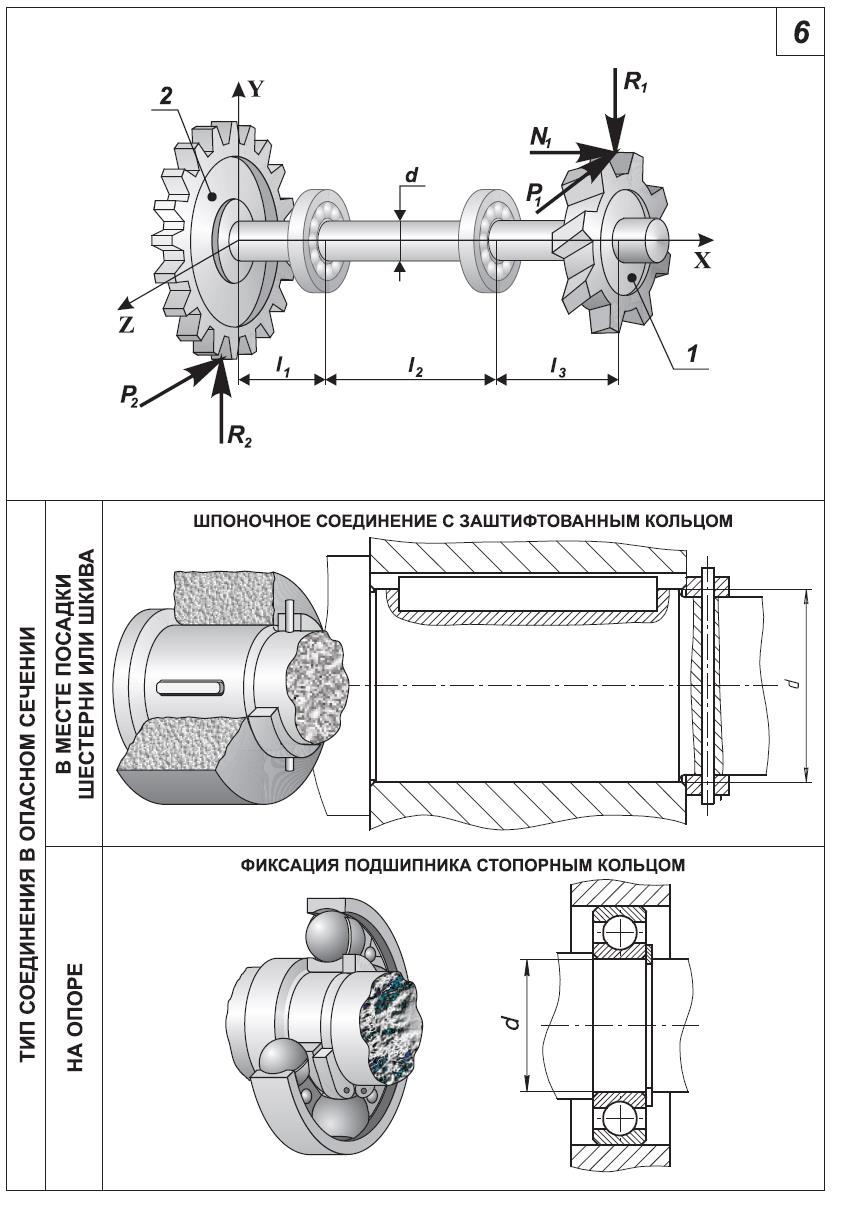
Рис. 1.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

Схема вала.

 

1. проектировочный расчет вала на

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

статическую прочность

 

При расчете на статическую прочность представим вал AD в виде балки на двух опорах. Одну из опор примем как неподвижный шарнир (сечение B ), другую, как наиболее близко расположенную к коническому колесу, – как подвижный шарнир (сечение C ) (рис. 2, а).

Определим крутящие сосредоточенные моменты действующие в сечениях A и D соответственно:

;  .

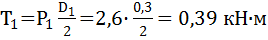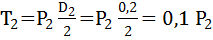    Для определения окружного усилия Р₂ запишем уравнение статического равновесия в виде суммы моментов всех сил, действующих на вал, относительно продольной оси х:

        

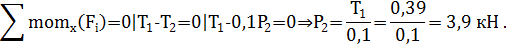
    Перенесем вектор силы N₁ на ось вала. При этом в сечении D возникнет сосредоточенный изгибающий момент:

   

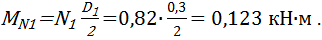
Радиальное усилие R₂ найдем по формуле:

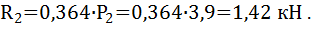
    Силовые факторы, лежащие в вертикальной плоскости, вызовут в подшипниках реакции  и 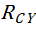, а в горизонтально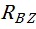й –  и 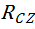 . Величины этих реакций определим, как для балки, лежащей на двух опорах.

    1.2. Построение эпюр внутренних силовых факторов

    Видно (рис. 2, а), что вал работает на совместное действие растяжения (сжатия), кручения и изгиба в вертикальной (ух) и горизонтальной (zx) плоскостях. Рассмотрим каждую деформацию отдельно, используя принцип независимости действия сил.

    Определим опасную точку вала. Для этого установим, как меняются подлине вала внутренние силовые факторы, т. е. построим их эпюры.

        

    Растяжение (сжатие).Вал нагружен двумя сосредоточенными продольными силами: N₁ и реакцией 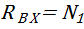 опоры B (рис. 2, б), которые вызывают на участке BD растяжение- сжатие (растяжение). Построим эпюру нормальных сил Э N (рис. 2, в).

    Кручение. Два скручивающих моме

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

нта T₁ и Т₂ (рис. 2, г) вызывают кручение на участке AD . Эпюру крутящих моментов ЭТ строим так же, как и при чистом кручении (рис. 2, д).

    Изгиб в вертикальной плоскости yх (рис. 1, е). Эпюра ЭМ_Z изгибающих моментов относительно оси z строится от сил  ,  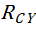, R₂, -R₁ и изгибающего момента M_{N 1} , действующих в вертикальной плоскости. Из уравнений статического равновесия определим  ,  :

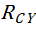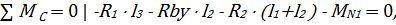
Откуда выражаем:

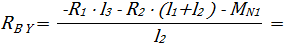
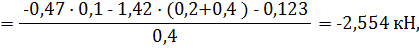
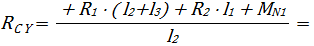
        Выполним проверку:

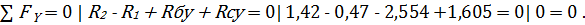
Следовательно, реакции 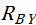 ,  определены верно!

 

Так как балка нагружена только сосредоточенными силовыми факторами, то изгибающий момент M _Z на всех участках будет постоянен или меняться по линейному закону.

 

Вычислим изгибающие моменты M _Z в сечениях A, B, C и D:

M _A ^Z =0 ;

M _B1 ^Z = R₂ · l₁ = 1,42 · 0,2 =0,284 кН·м ;

M _C1 ^Z = R₂ · (l₁+l₂)+Rd · l₂ = 1,42 · (0,2+0,4) - 2,554 · 0,4 =-0,17 кН·м ;

M _D ^Z = R₂ · (l₁+l₂+l₃)+Rd · (l₂+l₃)+R₂c · l₃ = 1,42 · (0,2+0,4+0,1) - 2,554 · (0,4+0,1)+ 1,605 · 0,1 =-0,123 кН·м .

    По полученным значениям строим эпюру ЭM _Z (рис. 2, ж).

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

Изгиб в горизонтальной плоскости zx (рис. 2, з). Эпюра ЭМ_Y изгибающих моментов относительно оси y строится от сил -P₂, -P₁ . Из уравнений статического равновесия определим  ,  :

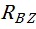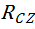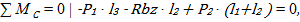
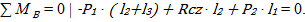
Откуда выражаем:

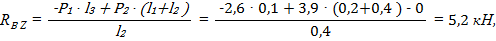
    Выполним проверку:

   

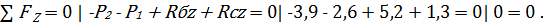
    Следовательно, реакции 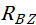 ,  определены верно!

Так как балка нагружена только сосредоточенными силовыми факторами, то изгибающий момент M _Y на всех участках будет постоянен или меняться по линейному закону.

Вычислим изгибающие моменты M _Y в сечениях A, B, C и D:

M _A ^Y =0 ;

M _B1 ^Y = -P₂ · l₁ = -3,9 · 0,2 = -0,78 кН·м ;

M _C1 ^Y = -P₂ · (l₁+l₂)+Rd · l₂ = -3,9 · (0,2+0,4)+ 5,2 · 0,4 =-0,26 кН·м ;

M _D ^Y = -P₂ · (l₁+l₂+l₃)+Rd · (l₂+l₃)+R4c · l₃ = -3,9 · (0,2+0,4+0,1)+ 5,2 · (0,4+0,1)+ 1,3 · 0,1 =0 .

    По полученным значениям строим эпюру ЭM _Y (рис. 2, и).

Построение эпюры суммарных изгибающих моментов.     Поскольку вал имеет круглое поперечное сечение, определим в сечениях величину суммарного изгибающего момента 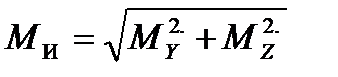. Тогда в сечениях A , B , C и D:

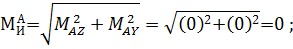
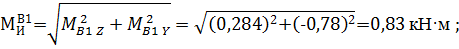
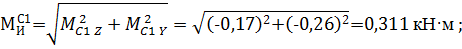
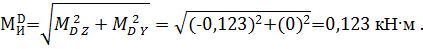
По полученным данным построим эпюру суммарных изгибающих моментов ЭM_и (рис. 2, к).

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

 

 

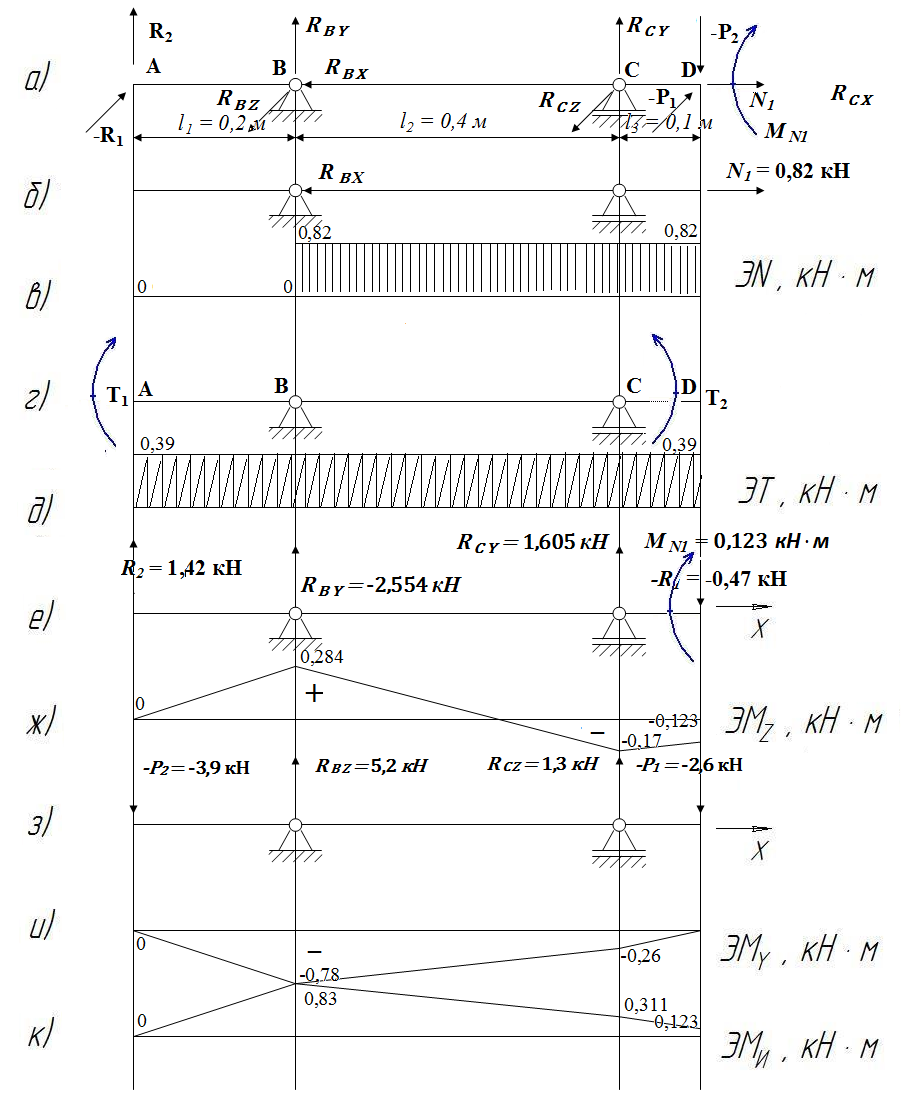
Рис. 2.
Расчет диаметра вала.

Для определения опасного сечения находим величины эквивалентных моментов по третьей теории прочности 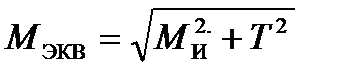. Тогда в сечениях A , B , C и D:

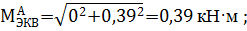
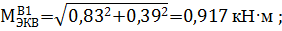
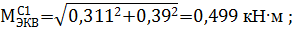
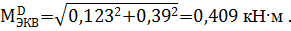
     Анализ результатов показывает, что опасным является сечение B, в котором эквивалентный момент достигает максимального значения и равен M _ЭКВМАХ =0,917 кН · м .

    Найдем допускаемое напряжение 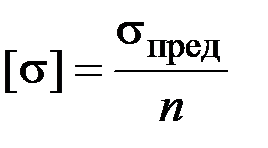. Так как сталь 15ХС пластична, то за s_пред принимаем предел текучести s_Т.. Согласно табл. П3 для стали 15ХС ГОСТ 1050-60 s_Т = 250 МПа , коэффициент запаса для пластичных материалов n = 1,5¸2,5. Примем n = 2. Тогда

    Из условия прочности:

,

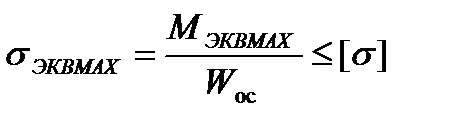где 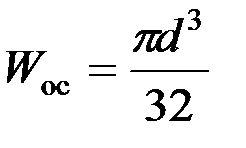 – осевой момент сопротивления для круглого поперечного се

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

чения диаметром d.

    Определим расчетный диаметр вала:

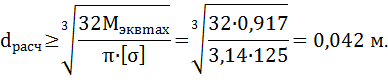
     В соответствии ГОСТ 6636-69 Ra40 принимаем d=45 мм.

     Вычислим геометрические характеристики этого сечения:

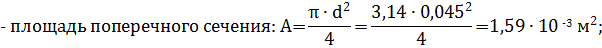
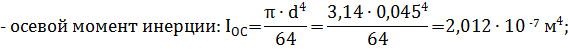
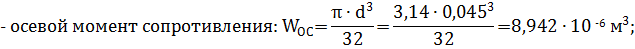
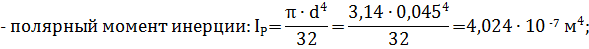
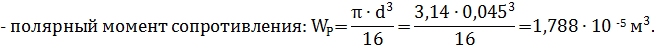
Рассмотрим опасное сечение вала B, в котором действуют суммарный изгибающий момент М_и = 0,83 кН·м , крутя

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

щий момент Т = 0,47 кН·м и продольная сила N = 0,82 кН (рис. 3, а).

Нормальные напряжения от изгиба  на внешних волокнах равны:

Нормальные напряжения от растяжения определим как

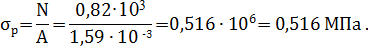
Касательные напряжения τ на контуре сечения равны:

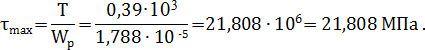
    Построим эпюры этих напряжений Э 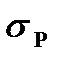, Э , Э  (рис. 3, б).

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

В опасной точке А сечения B имеет место плоское напряженное состояние (рис. 3, в). В этой точке действуют максимальные эквивалентные напряжения  s_{экв max}.

Определим их по III теории прочности:

    Условие прочности  выполняется, так как

103,035 МПа < 125 МПа.

     Определим недогрузку вала, учитывая, что диаметр вала выбран больше расчетного:

Недогрузка D_s меньше допустимого значения 15%. Таким образом, диаметр вала d = 45 мм из условия статической прочности подобран правильно.

 

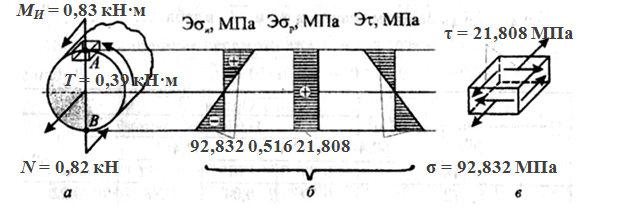
Рис. 3.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1054 02 0623 000 РР

Расчет вала на жесткость

     В расчетах примем модуль упругости (стали) E = 210 ГПа. Жесткость сечения равна:

    

     Для определения перемещений используем способ Верещагина [2].