Теорема Котельникова утверждает, что двумерный сигнал s(x,y){\displaystyle s(x,y)\!} с финитным спектром ~s(νx,νy){\displaystyle {\tilde {s}}(\nu _{x},\nu _{y})\!} можно восстановить без потери.

Доказательство теоремы проведем для частного случая, когда спектр отличен от нуля в прямоугольной областиDν=f|νx|⩽νmaxx=ν1,|νy|⩽νmaxy=ν2g{\displaystyle D_{\nu }={\mathcal {f}}|\nu _{x}|\leqslant \nu _{x}^{max}=\nu _{1},|\nu _{y}|\leqslant \nu _{y}^{max}=\nu _{2}{\mathcal {g}}\!} . В этом случае сигнал можно с любой степенью точности представить в виде дискретной суммы значений (отсчетов), взятых через конечные промежутки △x=1/2νx{\displaystyle \vartriangle x=1/2\nu _{x}\!}, △y=1/2νy{\displaystyle \vartriangle y=1/2\nu _{y}\!}. Эту теорему называют также теоремой о дискретном представлении, или теоремой отсчетов, или теоремой выборки.

Пусть задан финитный спектр (рис. 1):

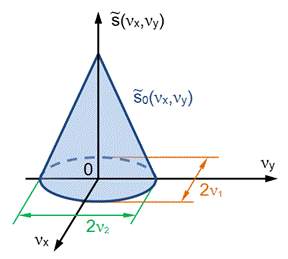
Рис. 1. Геометрическая модель двумерного пространственно-частотного спектра (ПЧС) финитной функции ¯s(νx,νy){\displaystyle {\bar {s}}(\nu _{x},\nu _{y})\!}

~s(νx,νy)={~s0(νx,νy),(νx,νy)∈Dν0,(νx,νy)∉Dν{\displaystyle {\tilde {s}}(\nu _{x},\nu _{y})={\begin{cases}{\tilde {s}}_{0}(\nu _{x},\nu _{y}),&(\nu _{x},\nu _{y})\in D_{\nu }\\0,(\nu _{x},\nu _{y})\notin D_{\nu }\end{cases}}\!}

Далее введем в рассмотрение выборочную функцию

svb(x,y)=s(x,y)comb(2ν1x,2ν2y) (1){\displaystyle s_{vb}(x,y)=s(x,y)\operatorname {comb} (2\nu _{1}x,2\nu _{2}y)\quad \quad ~\color {Maroon}(1)\!}

фурье-образ которой ~svb(νx,νy){\displaystyle {\tilde {s}}_{vb}(\nu _{x},\nu _{y})\!} равен двумерной бесконечной периодической сумме (рис. 2) дискретно смещенных финитных спектров исходного сигнала ~s0(νx,νy){\displaystyle {\tilde {s}}_{0}(\nu _{x},\nu _{y})\!}.

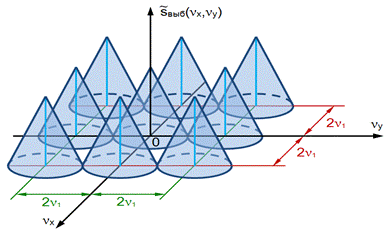
Рис. 2. Геометрическая модель двумерного ПЧС выборочной функции ¯svb(νx,νy){\displaystyle {\bar {s}}_{vb}(\nu _{x},\nu _{y})\!}

Таким образом,

~svb(νx,νy)=~s(νx,νy)⊗(1/(4ν1ν2))comb(νx/2ν1,νy/2ν2) (2){\displaystyle {\tilde {s}}_{vb}(\nu _{x},\nu _{y})={\tilde {s}}(\nu _{x},\nu _{y})\otimes (1/(4\nu _{1}\nu _{2}))\operatorname {comb} (\nu _{x}/2\nu _{1},\nu _{y}/2\nu _{2})\quad \quad ~\color {Maroon}(2)\!}

Тогда исходный финитный спектр ~s(νx,νy){\displaystyle {\tilde {s}}(\nu _{x},\nu _{y})\!} , показанный на рис. 1 можно представить в виде произведения фурье-образа выборочной функции (2){\displaystyle \color {Maroon}(2)\!} и двумерного прямоугольного импульса

~s(νx,νy)=~svb(νx,νy)rect(νx/2ν1,νy/2ν2) (3){\displaystyle {\tilde {s}}(\nu _{x},\nu _{y})={\tilde {s}}_{vb}(\nu _{x},\nu _{y})\operatorname {rect} (\nu _{x}/2\nu _{1},\nu _{y}/2\nu _{2})\quad \quad ~\color {Maroon}(3)\!}

В результате обратного преобразования Фурье из (3){\displaystyle \color {Maroon}(3)\!} с учетом (2){\displaystyle \color {Maroon}(2)\!} найдем

s(x,y)=F−1f~s(νx,νy)g=(1/(4ν1ν2))F−1f~s(νx,νy)⊗comb(νx/2ν1,νy/2ν2)g⊗F−1rect(νx/2ν1,νy/2ν2){\displaystyle s(x,y)=F^{-1}{\mathcal {f}}{\tilde {s}}(\nu _{x},\nu _{y}){\mathcal {g}}=(1/(4\nu _{1}\nu _{2}))F^{-1}{\mathcal {f}}{\tilde {s}}(\nu _{x},\nu _{y})\otimes \operatorname {comb} (\nu _{x}/2\nu _{1},\nu _{y}/2\nu _{2}){\mathcal {g}}\otimes F^{-1}\operatorname {rect} (\nu _{x}/2\nu _{1},\nu _{y}/2\nu _{2})\!}.

Откуда после преобразований, основанных на свойствах:

преобразование Фурье (как прямое, так и обратное) от свертки двух функций соответствует произведению их Фурье-образов;

преобразование Фурье от гребенчатой функции – гребенчатая функция;

фильтрующее свойство дельта-функции,

можно записать:

s(x,y)=4ν1ν2∞∬−∞s(u,v)∞∑k,n=−∞δ(2ν1u−k,2ν2v−n)×sinc[2πν1(x−u),2πν2(y−v)]dudv{\displaystyle s(x,y)=4\nu _{1}\nu _{2}\iint \limits _{-\infty }^{\infty }s(u,v)\sum _{k,n=-\infty }^{\infty }\delta (2\nu _{1}u-k,2\nu _{2}v-n)\times \operatorname {sinc} [2\pi \nu _{1}(x-u),2\pi \nu _{2}(y-v)]dudv\!}

Переставляя местами двойной интеграл и двойную сумму, с учетом фильтрующего свойства δ{\displaystyle \delta \!}-функции получим окончательное выражение для ряда Котельникова

s(x,y)=∞∑k,n=−∞s(k/2ν1,n/2ν2)sincf2πν1[x−(k/2ν1)],2πν2[y−(n/2ν2)]g=4ν1ν2svb(x,y)⊗sinc(π2ν1x,π2ν2y) (4){\displaystyle s(x,y)=\sum _{k,n=-\infty }^{\infty }s(k/2\nu _{1},n/2\nu _{2})\operatorname {sinc} {\mathcal {f}}2\pi \nu _{1}[x-(k/2\nu _{1})],2\pi \nu _{2}[y-(n/2\nu _{2})]{\mathcal {g}}=4\nu _{1}\nu _{2}s_{vb}(x,y)\otimes \operatorname {sinc} (\pi 2\nu _{1}x,\pi 2\nu _{2}y)\quad \quad ~\color {Maroon}(4)\!}

где 1/2ν1=△x{\displaystyle 1/2\nu _{1}=\vartriangle x\!},

1/2ν2=△y{\displaystyle 1/2\nu _{2}=\vartriangle y\!}.

Выражение (4){\displaystyle \color {Maroon}(4)\!} представляет сигнал с финитным спектром в виде бесконечной двойной суммы sinc{\displaystyle \operatorname {sinc} \!}-образных базисных сигналов. Иначе говоря, для восстановления сигнала s(x,y){\displaystyle s(x,y)\!} необходимо вычислить бесконечную двойную сумму в виде линейной комбинации сигналов sincf2πν1[x−(k/2ν1)],2πν2[y−(n/2ν2)]g{\displaystyle \operatorname {sinc} {\mathcal {f}}2\pi \nu _{1}[x-(k/2\nu _{1})],2\pi \nu _{2}[y-(n/2\nu _{2})]{\mathcal {g}}\!} с амплитудой s(k/2ν1,n/2ν2){\displaystyle s(k/2\nu _{1},n/2\nu _{2})\!} из совокупности выборочных значений. Восстановление сигналов осуществляется в результате последовательного сдвига функций в точке (k/2ν1,n/2ν2){\displaystyle (k/2\nu _{1},n/2\nu _{2})\!} . Базисный сигнал sinc(π2ν1x,π2ν2y){\displaystyle \operatorname {sinc} (\pi 2\nu _{1}x,\pi 2\nu _{2}y)\!} называют интерполяционной функцией, или функцией отсчетов. График ряда Котельникова для одномерного сигнала s(x,0){\displaystyle s(x,0)\!} приведен на рис. 3.

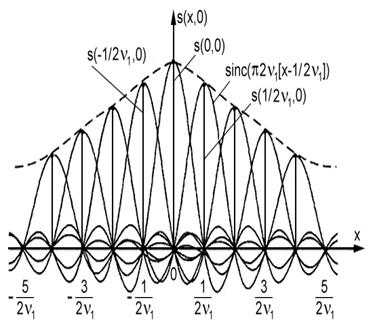
Рис. 3. Двумерная геометрическая модель, идентифицирующая одномерный восстановленный сигнал в виде суммы sinc{\displaystyle \operatorname {sinc} \!}-образных базисных типовых сигналов

Для одномерного временного сигнала s(t){\displaystyle s(t)\!} с финитным спектром, отличным от нуля на интервале |νt|⩽νmaxt=νm{\displaystyle |\nu _{t}|\leqslant \nu _{t}^{max}=\nu _{m}\!} , ряд Котельникова имеет вид

s(t)=∞∑k=−∞s(k/2νm)sincf2πνm[t−(k/2νm)]g{\displaystyle s(t)=\sum _{k=-\infty }^{\infty }s(k/2\nu _{m})\operatorname {sinc} {\mathcal {f}}2\pi \nu _{m}[t-(k/2\nu _{m})]{\mathcal {g}}\!}

При этом для восстановления сигнала s(t){\displaystyle s(t)\!} в каждой точке выборки k/2νm{\displaystyle k/2\nu _{m}\!} строится интерполяционная функция sinc(2πνmt){\displaystyle \operatorname {sinc} (2\pi \nu _{m}t)\!} с амплитудой s(k/2νm){\displaystyle s(k/2\nu _{m})\!}.

Строго говоря, сигналов с финитным спектром не существует. Однако для большинства реальных сигналов спектральная плотность на высоких частотах ничтожно мала. Поэтому большая часть энергии сигнала локализована в ограниченной частотной области, а сам сигнал хорошо аппроксимируется функцией с финитным спектром. Погрешность, возникающая при отбрасывании высших частотных гармоник, пренебрежимо мала.

Свойства выборочной функции

svb(x,y)=s(x,y)comb(2ν1x,2ν2y)=(1/(4ν1ν2))∞∑k,n=−∞s(k/2ν1,n/2ν2)δ[x−(k/2ν1),y−(n/2ν2)] (5){\displaystyle s_{vb}(x,y)=s(x,y)\operatorname {comb} (2\nu _{1}x,2\nu _{2}y)=(1/(4\nu _{1}\nu _{2}))\sum _{k,n=-\infty }^{\infty }s(k/2\nu _{1},n/2\nu _{2})\delta [x-(k/2\nu _{1}),y-(n/2\nu _{2})]\quad \quad ~\color {Maroon}(5)\!}

Функция (1){\displaystyle \color {Maroon}(1)\!} называемая выборочной функцией, представляет собой двумерную δ{\displaystyle \delta \!} - решётку из функций δ[x−(k/2ν1),y−(n/2ν2)]{\displaystyle \delta [x-(k/2\nu _{1}),y-(n/2\nu _{2})]\!}с амплитудой (1/(4ν1ν2))×s(k/2ν1,n/2ν2){\displaystyle (1/(4\nu _{1}\nu _{2}))\times s(k/2\nu _{1},n/2\nu _{2})\!}. Рассмотрим её основные свойства:

Функция svb{\displaystyle s_{vb}\!} имеет размерность исходного сигнала s{\displaystyle s\!}.

Объем выборки пропорционален сумме выборочных значений

∞∬−∞svb(x,y)dxdy=(1/(4ν1ν2))∞∑k,n=−∞∞∬−∞s(x,y)δ[x−(k/2ν1),y−(n/2ν2)]dxdy=(1/(4ν1ν2))∞∑k,n=−∞s(k/2ν1,n/2ν2){\displaystyle \iint \limits _{-\infty }^{\infty }s_{vb}(x,y)dxdy=(1/(4\nu _{1}\nu _{2}))\sum _{k,n=-\infty }^{\infty }\iint \limits _{-\infty }^{\infty }s(x,y)\delta [x-(k/2\nu _{1}),y-(n/2\nu _{2})]dxdy=(1/(4\nu _{1}\nu _{2}))\sum _{k,n=-\infty }^{\infty }s(k/2\nu _{1},n/2\nu _{2})\!}

Спектр выборочной функции равен бесконечной двумерной сумме дискретно смещенных финитных спектров исходного сигнала и совпадает со вспомогательной функцией (2){\displaystyle \color {Maroon}(2)\!} на рис. 2, так что

~svb(νx,νy)=∞∑k,n=−∞~s(νx−k2ν1,νy−n2ν2){\displaystyle {\tilde {s}}_{vb}(\nu _{x},\nu _{y})=\sum _{k,n=-\infty }^{\infty }{\tilde {s}}(\nu _{x}-k2\nu _{1},\nu _{y}-n2\nu _{2})\!}. (6){\displaystyle \quad \quad \color {Maroon}(6)\!}

Свёртка 4ν1ν2svb(x,y){\displaystyle 4\nu _{1}\nu _{2}s_{vb}(x,y)\!} с интерполяционной функцией sinc(π2ν1x,π2ν2y){\displaystyle \operatorname {sinc} (\pi 2\nu _{1}x,\pi 2\nu _{2}y)\!} восстанавливает исходный сигнал с помощью ряда Котельникова (4){\displaystyle \color {Maroon}(4)\!}, который можно записать в виде s(x,y)−4ν1ν2svb(x,y)⊗sinc(π2ν1x,π2ν2y){\displaystyle s(x,y)-4\nu _{1}\nu _{2}s_{vb}(x,y)\otimes \operatorname {sinc} (\pi 2\nu _{1}x,\pi 2\nu _{2}y)\!}.

На практике часто используют выборочную функцию s′vb(x,y)=4ν1ν2s(x,y)comb(2ν1x,2ν2y){\displaystyle s'_{vb}(x,y)=4\nu _{1}\nu _{2}s(x,y)\operatorname {comb} (2\nu _{1}x,2\nu _{2}y)\!}, отличающуюся от (4){\displaystyle \color {Maroon}(4)\!} постоянным коэффициентом. Ее свойства совпадают со свойствами функции svb(x,y){\displaystyle s_{vb}(x,y)\!}.

Переналожение спектров

Пусть выборка осуществляется через произвольные промежутки △x⩽1/2ν1{\displaystyle \vartriangle x\leqslant 1/2\nu _{1}\!}, т.е. 1/△x⩾2ν1{\displaystyle 1/\vartriangle x\geqslant 2\nu _{1}\!} ; △y⩽1/2ν2{\displaystyle \vartriangle y\leqslant 1/2\nu _{2}\!}, т.е. 1/△y⩾2ν2{\displaystyle 1/\vartriangle y\geqslant 2\nu _{2}\!} . В этом случае вспомогательная функция (2){\displaystyle \color {Maroon}(2)\!} имеет вид

<center>~svb(νx,νy)=~s(νx,νy)⊗(△x,△y)comb(△xνx,△yνy) (2′){\displaystyle {\tilde {s}}_{vb}(\nu _{x},\nu _{y})={\tilde {s}}(\nu _{x},\nu _{y})\otimes (\vartriangle x,\vartriangle y)\operatorname {comb} (\vartriangle x\nu _{x},\vartriangle y\nu _{y})\quad \quad ~\color {Maroon}(2')\!}

Подставляя ее в (3){\displaystyle \color {Maroon}(3)\!}, в результате обратного преобразования Фурье получим выражение для обобщенного ряда Котельникова

s(x,y)=4ν1ν2△x△y∞∑k,n=−∞s(k△x,n△y)×sinc[2πν1(x−k△x),2πν2(y−n△y)] (4′){\displaystyle s(x,y)=4\nu _{1}\nu _{2}\vartriangle x\vartriangle y\sum _{k,n=-\infty }^{\infty }s(k\vartriangle x,n\vartriangle y)\times \operatorname {sinc} [2\pi \nu _{1}(x-k\vartriangle x),2\pi \nu _{2}(y-n\vartriangle y)]\quad \quad ~\color {Maroon}(4')\!}

которое при △x=1/2ν1{\displaystyle \vartriangle x=1/2\nu _{1}\!}, △y=1/2ν2{\displaystyle \vartriangle y=1/2\nu _{2}\!} переходит в ряд Котельникова (4){\displaystyle \color {Maroon}(4)\!}.

Если теперь интервалы выборки △x>1/2ν1{\displaystyle \vartriangle x>1/2\nu _{1}\!}, т.е. 1/△x<2ν1{\displaystyle 1/\vartriangle x<2\nu _{1}\!} ; △y>1/2ν2{\displaystyle \vartriangle y>1/2\nu _{2}\!}, т.е. 1/△y<2ν2{\displaystyle 1/\vartriangle y<2\nu _{2}\!}, то для выборочной функции (5){\displaystyle \color {Maroon}(5)\!}имеем

svb(x,y)=s(x,y)comb(x/△x,y△y) (7){\displaystyle s_{vb}(x,y)=s(x,y)\operatorname {comb} (x/\vartriangle x,y\vartriangle y)\quad \quad ~\color {Maroon}(7)\!}

В свою очередь для спектра выборочной функции по аналогии с (6){\displaystyle \color {Maroon}(6)\!}

~svb(νx,νy)=∞∑k,n=−∞~s[νx−(k/△x),νy−(n/△y)] (2′′){\displaystyle {\tilde {s}}_{vb}(\nu _{x},\nu _{y})=\sum _{k,n=-\infty }^{\infty }{\tilde {s}}[\nu _{x}-(k/\vartriangle x),\nu _{y}-(n/\vartriangle y)]\quad \quad ~\color {Maroon}(2'')\!}

На рис. 4 (а,б) приведены одномерные спектры ~s(0,νy){\displaystyle {\tilde {s}}(0,\nu _{y})\!} и ~svb(0,νy){\displaystyle {\tilde {s}}_{vb}(0,\nu _{y})\!}.

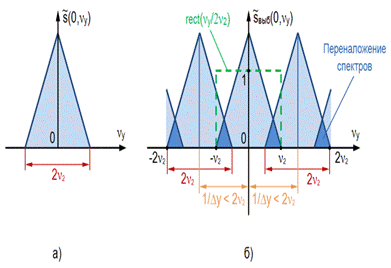
Рис. 4. Геометрическая модель двумерного одномерных пространственно-частотных спектров (ПЧС), идентифицирующая их переналожение: а- ПЧС входного сигнала; б - ПЧС выборочной функции при △y>1/2ν2{\displaystyle \vartriangle y>1/2\nu _{2}\!}

Так как

~svb(νx,νy)rect(νx/2ν1,νy/2ν2)≠~s(νx,νy){\displaystyle {\tilde {s}}_{vb}(\nu _{x},\nu _{y})\operatorname {rect} (\nu _{x}/2\nu _{1},\nu _{y}/2\nu _{2})\neq {\tilde {s}}(\nu _{x},\nu _{y})\!}, → (8){\displaystyle \to ~\color {Maroon}(8)\!}

то использование низкочастотного ПЧФ с передаточной функцией rect(νx/2ν1,νy/2ν2){\displaystyle \operatorname {rect} (\nu _{x}/2\nu _{1},\nu _{y}/2\nu _{2})\!} при передаче по каналу связи svb(x,y){\displaystyle s_{vb}(x,y)\!} в виде (7){\displaystyle \color {Maroon}(7)\!} не позволяет выделить спектр ~s(νx,νy){\displaystyle {\tilde {s}}(\nu _{x},\nu _{y})\!} исходного сигнала в чистом виде. В отфильтрованном спектре (8){\displaystyle \color {Maroon}(8)\!} будут присутствовать частоты от соседних налагающихся спектров ~s[νx±(1/△x),νy±(1/△y)]{\displaystyle {\tilde {s}}[\nu _{x}\pm (1/\vartriangle x),\nu _{y}\pm (1/\vartriangle y)]\!} (рис. 4б). В результате переналожения спектров возникают так называемые шумы дискретизации.