Кафедра «Математическое и компьютерное моделирование»
По дисциплине «Прикладной функциональный анализ»
Предназначен для обучающихся специальности 5B070500 - «Математическое и компьютерное моделирование»
1. Процесс ортогонализации Шмидта. Свойства скалярного произведения.
2. Ряды в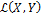 
, пространство 
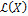. Сильная сходимость в .
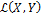3. Доказать, что множество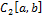 
всех непрерывных функций на сегменте 
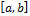, с расстоянием 
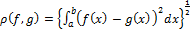является полным метрическим пространством.
Кафедра «Математическое и компьютерное моделирование»
По дисциплине «Прикладной функциональный анализ»
Предназначен для обучающихся специальности 5B070500 - «Математическое и компьютерное моделирование»
1. Принцип вложенных шаров, множества I и II категории.
2. Принцип равномерной ограниченности. Продолжение ЛО по непрерывности. Умножение элементов НП.
3. Докажите неравенство Гельдера: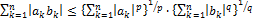 
, здесь числа 
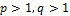удовлетворяют равенству 
.
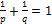Кафедра «Математическое и компьютерное моделирование»
По дисциплине «Прикладной функциональный анализ»
Предназначен для обучающихся специальности 5B070500 - «Математическое и компьютерное моделирование»
1. Определение и примеры линейных пространств. Линейная зависимость и независимость элементов. Конечномерные и бесконечномерные линейные пространства.
2. Теорема Хана-Банаха для ли нейных операторов.
3. Множество упорядоченных групп из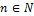 
действительных чисел 
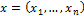с метрикой 
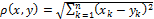пространство 
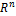является полным метрическим пространством. Доказать.
Кафедра «Математическое и компьютерное моделирование»
По дисциплине «Прикладной функциональный анализ»
Предназначен для обучающихся специальности 5B070500 - «Математическое и компьютерное моделирование»
1. Определение и примеры нормированных пространств. Неравенства Гельдера и Минковского для сумм.
2. Теорема Ф. Рисса об общем виде линейных функционалов в гильбертовом пространстве.
3. В пространство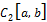 
, состоящего из непрерывных на 
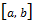действительных функций, со скалярным произведением 
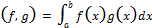, дана тригонометрическая система 
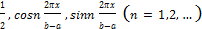является ортогональной.Нормировать данную систему.
Кафедра «Математическое и компьютерное моделирование»
По дисциплине «Прикладной функциональный анализ»
Предназначен для обучающихся специальности 5B070500 - «Математическое и компьютерное моделирование»
1. Примеры пространств со скалярным произведением. Пространство кусочно непрерывных функций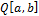 
.
2. Нормированное пространство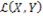 
, норма ЛО. Равномерная сходимость ЛО.
3. Разложите функцию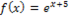 
в сегменте 
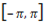в ряд Фурье по тригонометрической системе.
Кафедра «Математическое и компьютерное моделирование»
По дисциплине «Прикладной функциональный анализ»
Предназначен для обучающихся специальности 5B070500 - «Математическое и компьютерное моделирование»
1. Процесс ортогонализации Шмидта. Свойства скалярного произведения.
2. Ряды в 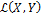, пространство 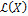. Сильная сходимость в .
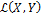3. Доказать, что множество 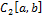всех непрерывных функций на сегменте 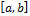, с расстоянием 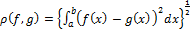является полным метрическим пространством.
Дата: 2019-05-28, просмотров: 124.
