Допустим передаточная функция разомкнутой системы имеет вид:

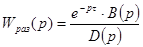                                             (2.4.1.1)

где В(р)- полином числителя, а D(р) – характеристический полином передаточной функции разомкнутой системы без запаздывания, то передаточная функция замкнутой системы регулирования будет иметь вид

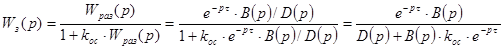     (2.4.1.2)

Характеристическое уравнение включает в себя функцию 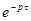и имеет трансцендентный вид:

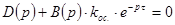                                          (2.4.1.3)

Использовать такое характеристическое уравнение для определения устойчивости по корням уравнения или по критериям Гурвица или Михайлова прямым способом невозможно.

Вместе с тем определять устойчивость по корням характеристического уравнения или по критериям Гурвица и Михайлова можно, если приближенно заменить величину 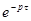 разложением ее в дробный ряд Пада, отбросив члены со степенью рτ два и более:

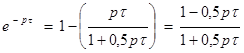                                       (2.4.1.4)

Если подставить выражение (2.4.1.4) в характеристическое уравнение замкнутой системы регулирования (2.4.1.3), то получится характеристическое уравнение в обычном полиноминальном виде:

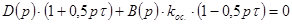                               (2.4.1.5)

В таком виде уравнение может быть решено и по значениям его корней можно определить устойчивость замкнутой системы регулирования, а само уравнение можно использовать для построения годографа Михайлова.

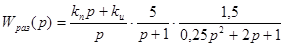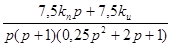=       (2.4.1.6)

Передаточная функция для замкнутой системы имеет вид:

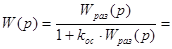
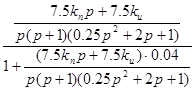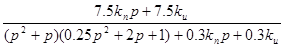=                              (2.4.1.7)

Характеристическое уравнение системы имеет вид:

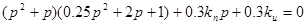                                      (2.4.1.8)

Для проверки устойчивости системы при принятых параметрах регулятора (k_п=6 и k_и=2) данные значения нужно подставить в (2.4.1.3):

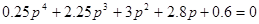                                                  (2.4.1.9)

Согласно критерию Гурвица необходимым условием устойчивости системы является положительность всех коэффициентов характеристического уравнения. Согласно (35) оно выполнено. Кроме того, для устойчивости данной системы четвертого порядка необходимо, чтобы определитель третьего порядка также был положителен:

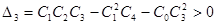,                                                           (2.4.1.10)

где 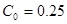, , 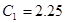, , 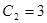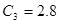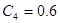- коэффициенты характеристического уравнения.

Значение данного определителя

,

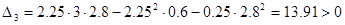что подтверждает устойчивость системы.

Используя формулы (2.4.1.1) - (2.4.1.10) рассчитать и проверить устойчивость замкнутой системы при помощи алгебраического критерия Гурвица.

2.3.2 Исследование замкнутой системы на устойчивость с  использованием годографа Михайлова

Оставив в уравнении (2.4.1.9) в качестве переменных величин параметры ПИ-регулятора, получим характеристическое уравнение системы в виде:

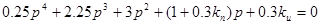.                                       (2.4.2.1)

Заменяем p на jω получаем характеристический полином:

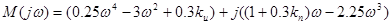                       (2.4.2.2)

где 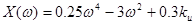                                                                           (2.4.2.3)

действительная функция Михайлова, а

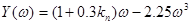                                                                              (2.4.2.4)

 мнимая функция Михайлова.

Согласно критерию Михайлова система 4 порядка устойчива, если годограф Михайлова при изменении частоты ω от 0 до +∞, начинаясь при ω=0 на вещественной положительной полуоси, обходит против часовой стрелки последовательно 4 квадранта координатной плоскости, нигде не проходя через начало координат. На рис. 20 представлен годограф Михайлова при выбранных значениях параметров ПИ-регулятора: k_п=6 и k_и=2.

Используя формулы (37) - (40) рассчитать и проверить устойчивость замкнутой системы при помощи критерия Михайлова.

В программной среде VisSim построим модель годографа Михайлова показанной на рисунке 25.

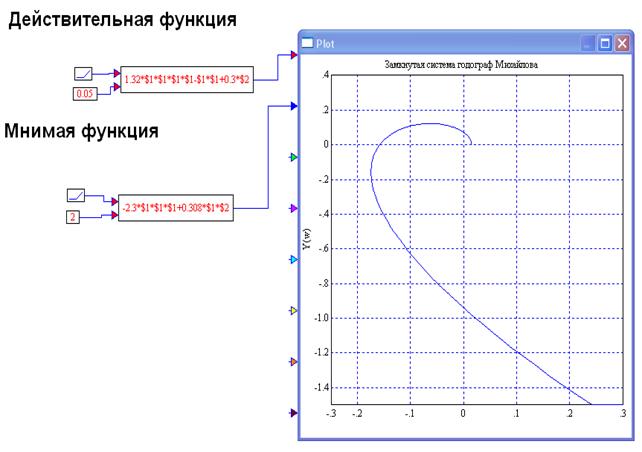
Рисунок 25 - Модель построения Годографа Михайлова