Элементы абстрактного массива в памяти машины физически располагаются последовательно, согласно описанию. При этом каждый элемент занимает в памяти количество байт, соответствующее его размеру. Например, если массив состоит из элементов типа integer , то каждый элемент будет занимать по два байта. А весь массив займет S^2 байта, где S – количество элементов в массиве.

А сколько места займет массив, состоящий из массивов, т.е. матрица? Очевидно: S i^S j , где S i - количество строк, а S j – количество элементов в каждой строке. Например, для массива типа

Matrix = array [1..3, 1..2] of integer ;

потребуется 12 байт памяти.

Как будут располагаться в памяти элементы этого массива? Рассмотрим схему размещения массива M типа matrix в памяти.

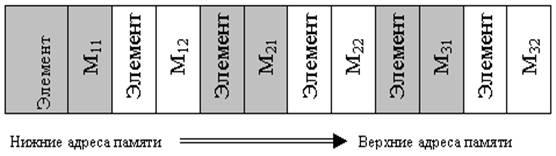
Под каждый элемент M [i,j] типа integer выделяется две ячейки памяти. Размещение в памяти осуществляется «снизу вверх». Элементы размещаются в порядке изменения индекса, что соответствует схеме вложенных циклов: сначала размещается первая строка, затем вторая, третья... Внутри строки по порядку идут элементы: первый, второй и т.д.

Как мы знаем, доступ к любой переменной возможен, только если известен адрес ячейки памяти, в которой хранится переменная. Конкретная память выделяется для переменной при загрузке программы, то есть устанавливается взаимное соответствие между переменной и адресом ячейки. Но если мы объявили переменную как массив, то программа «знает» адрес начала массива, то есть первого его элемента. Как же происходит доступ ко всем другим элементам массива?

При реальном доступе к ячейке памяти, в которой хранится элемент двумерного массива, система вычисляет ее адрес по формуле:

Addr + Size Elem * Cols *( I -1)+ Size Elem *( J -1),

где Addr – фактический начальный адрес, по которому массив располагается в памяти; I , J – индексы элемента в двумерном массиве; SizeElem – размер элемента массива (например, два байта для элементов типа integer ); Cols – количество элементов в строке.

Выражение SizeElem * Cols *( I -1)+ SizeElem *( J -1) называют смещением относительно начала массива.

Примеры решения задач с двумерными массивами Паскаля

Задача: Найти произведение ненулевых элементов матрицы.

Решение:

Для решения данной задачи нам потребуются переменные: матрица, состоящая, например, из целочисленных элементов; P – произведение элементов, отличных от 0; I , J – индексы массива; N , M – количество строк и столбцов в матрице. Входными данными являются N , M – их значения введем с клавиатуры; матрица – ввод матрицы оформим в виде процедуры, заполнение матрицы осуществим случайным образом, т.е. с помощью функции random (). Выходными данными будет являться значение переменной P (произведение). Чтобы проверить правильность выполнения программы, необходимо вывести матрицу на экран, для этого оформим процедуру вывода матрицы. Ход решения задачи:

обсудим сначала выполнение основной программы, реализацию процедур обговорим чуть позже:

введем значения N и M ; Введем двумерный массив Паскаля, для этого обращаемся к процедуре vvod ( a ), где а – матрица; Напечатаем полученную матрицу, для этого обращаемся к процедуре print ( a ); Присвоим начальное значение переменной P =1; Будем последовательно перебирать все строки I от 1-й до N -й, в каждой строке будем перебирать все столбцы J от 1-го до M -го, для каждого элемента матрицы будем проверять условие: если a ij ? 0, то произведение P будем домножать на элемент a ij ( P = P * a ij ); Выведем на экран значение произведения ненулевых элементов матрицы – P ;

А теперь поговорим о процедурах.

Замечание (это важно!) Параметром процедуры может быть любая переменная предопределенного типа, это означает, что для передачи в процедуру массива в качестве параметра, тип его должен быть описан заранее. Например :

Type

Matrix=array [1..10, 1..10] of integer;

..............................