Силовой анализ механизма заключается в нахождении неизвестных сил и моментов, приложенных к каждому звену исследуемого механизма, в частности реакции в кинематических парах.
Чтобы выполнить силовой расчет необходимо определить внешние силы и моменты сил действующих на звенья механизма (движущая сила, силы полезного сопротивления, силы тяжести или сопротивление среды).
Возникновение реакции в кинематических парах обусловлено не только воздействием внешних сил, но и движением звеньев с ускорениями.
Расчет ведем по методу Д'Аламбера, который формулируется следующим образом:
Если к внешним силам, действующим на механические системы, прибавить силы инерции, то такую систему можно рассматривать условно находящуюся в равновесии.
Целью данного раздела является определение реакции в кинематических парах. Расчет ведется в порядке обратном кинематическому анализу, т.е. расчет начинаем с группы наиболее удаленной от ведущего звена.
2.1 Вычерчиваем в масштабе 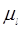 кинематическую схему механизма соответствующую min и max значениям приведенного момента Мспр сил сопротивления:
кинематическую схему механизма соответствующую min и max значениям приведенного момента Мспр сил сопротивления:
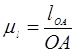 ,
,
где ОА – отрезок произвольно взятый на чертеже, мм.
Принимаем 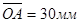
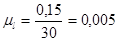
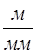
2.2 Составляем векторное уравнение для определения скорости в точке В.
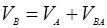 ;
;
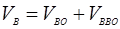 ,
,
где 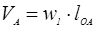 – абсолютная скорость точки А.
– абсолютная скорость точки А.
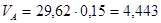 м/сек;
м/сек;
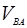 – относительная скорость точки В, направленная перпендикулярно шатуну АВ.
– относительная скорость точки В, направленная перпендикулярно шатуну АВ.
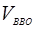 – относительная скорость точки В, направленная вдоль ползуна.
– относительная скорость точки В, направленная вдоль ползуна.
Определяем масштаб плана скоростей:
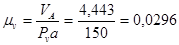 ;
;
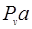 – произвольно взятый отрезок 150 мм.
– произвольно взятый отрезок 150 мм.
Строим план скоростей и с его помощью определенной скорости точек механизма и угловую скорость звена.
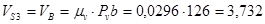 м/с
м/с
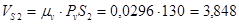 м/с
м/с
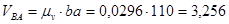 м/с
м/с
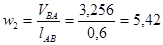 c-1.
c-1.
2.3 Для определения ускорений составляем систему векторов ускорений:

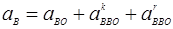 ,
,
где 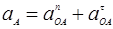 – ускорение точки А.
– ускорение точки А.
Ввиду того, что ∆wmax мала, принимаем, что кривошип вращается с постоянной угловой скоростью w1= const.
Угловое ускорение кривошипа 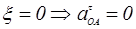 , тогда
, тогда 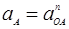 .
.
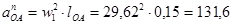 м/с-2;
м/с-2;
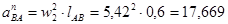 м/с-2;
м/с-2;
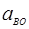 – вектор ускорения точки Во принадлежит стойке
– вектор ускорения точки Во принадлежит стойке 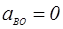
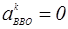 – вектор Кориолисова ускорения;
– вектор Кориолисова ускорения;
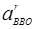 – вектор относительного ускорения, известен только по направлению.
– вектор относительного ускорения, известен только по направлению.
Определяем масштаб плана ускорений по формуле:
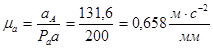
где 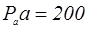 − выбираем произвольно.
− выбираем произвольно.
Построение плана ускорений помогает определить абсолютные и относительные ускорения точек и угловые ускорения звеньев механизма для выбранных положений.
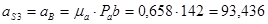 м/с -2;
м/с -2;
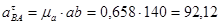 м/с-2;
м/с-2;
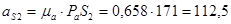 м/с-2;
м/с-2;
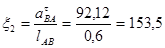 с-2
с-2
2.4 Определяем величины главных векторов сил инерции Ри и его главных моментов Ми:
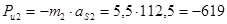 H;
H;
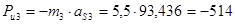 H;
H;
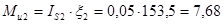
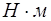 .
.
Момент сил инерции Mu2 заменим парой сил
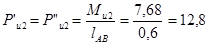 Н
Н
2.5 Определяем реакции в кинематических парах методом плана сил. Для этого вычерчиваем в масштабе l группу Ассура и прикладываем к ней силу Р; силы тяжести G2 и G3 и силы инерции Ри2 и Ри3; моменты сил инерции Mu2, реакцию R03; реакцию кривошипа на шатун R12, которую раскладываем на нормальную и тангенциальную.
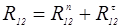
Реакцию 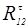 определим из уравнения равновесия моментов сил действующих на звено 2 (шатун АВ) относительно точки В.
определим из уравнения равновесия моментов сил действующих на звено 2 (шатун АВ) относительно точки В.
В уравнении берем слагаемые со знаком «+», если момент создаваемый силой направлен против часовой стрелки, и со знаком «–», если по часовой стрелки.
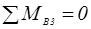
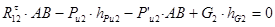
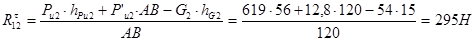
Записываем векторное уравнение всех сил:
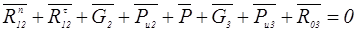
Значения сил
Таблица 5.
| Положения механизма | 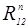
| 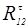
| 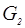
| 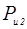
| 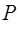
| 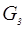
| 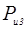
| 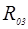
| 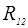
|
| 3 | 16500 | 295 | 54 | 619 | 17246 | 54 | 514 | 3200 | 16700 |
Неизвестные реакции 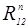 и
и 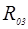 определим графическим построением плана сил в масштабе:
определим графическим построением плана сил в масштабе:
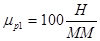 ;
;
Дата: 2019-05-28, просмотров: 283.