Содержание
Задание для курсового проектирования
Введение - цели и задачи курсового проектирования
1. Синтез и динамический анализ основного механизма
2. Силовой анализ рычажного механизма
3.Проектирование эвольвентного зубчатого зацепления
4. Синтез кулачкового механизма
Литература
Введение
Курсовой проект по дисциплине «Теория механизмов и машин» состоит из графической части и расчетно-пояснительной записки. Включает в себя четыре основных раздела:
1. Синтез и динамический анализ основного механизма.
2. Силовой анализ рычажного механизма.
3. Проектирование эвольвентного зубчатого зацепления и синтез планетарного механизма.
4. Синтез кулачкового механизма.
В первом разделе курсового проекта выполняется проектирования основного рычажного механизма, рассчитывается момент инерции маховика и определяется истинный закон движения звена приведения.
Во втором разделе рассчитываются силы и моменты инерции, приложенные к звеньям, определяются неизвестные реакции в кинематических парах и уравновешивающий момент.
В третьем разделе проводится расчет геометрических параметров, контрольных размеров, качественных и кинематических характеристик эвольвентного зубчатого зацепления. Проводится оценка спроектированной передачи по всем вышеизложенным параметрам. Исходные данные выбираются в соответствии с рекомендациями ГОСТ 16532-70. Здесь же выполняется синтез планетарного механизма.
В четвертом разделе проекта определяются основные параметры кулачкового механизма, и строится профиль кулачка, обеспечивающий заданный закон движения толкателя.
Графическая часть проекта выполняется на четырех листах формата А1 по разделам в соответствии с ГОСТ 2304-68 и ГОСТ 2302-68.
РАЗДЕЛ I
Синтез и динамический анализ основного механизма.
Целью данного раздела является проектирование основного кривошипно-шатунного механизма, определение длин его звеньев, расчет момента инерции маховика, определение истинного закона движения звена приведения.
1.1. По формуле Чебышева определим степень подвижности механизма:
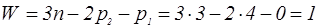
Согласно классификации Артоболевского механизм состоит из: механизма I класса - кривошип ОА, стойка О.
Структурная группа Ассура II класса, II порядка, II вида. - шатун АВ, ползун В; I(0;1) – II2 (2;3) – структурная форма механизма.
В целом механизм является механизмом II класса – по наивысшему.
1.2 По заданным исходным данным спроектируем основной кривошипно-шатунный механизм:
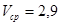 м/с;
м/с;
n1 = 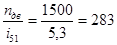 об/мин;
об/мин;
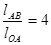
Для этого необходимо определить размеры звеньев, найти положения центров тяжести.
1.2.1. Длину кривошипа lОА вычисляем по формуле:
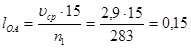 м
м
1.2.2. Определяем длину шатуна:
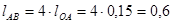 м
м
1.2.3. Определяем масштаб построения:
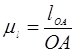 ,
,
где ОА – отрезок произвольно взятый на чертеже, мм.
Принимаем 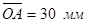
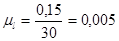
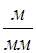
1.2.4. Определяем длину шатуна:
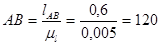 мм
мм
1.2.5.Определим положение центра масс шатуна:
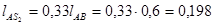 м
м
AS2 = 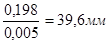
1.3 Вычерчиваем в масштабе диаграмму изменения давления, расположив ось абсцисс параллельно перемещению ползуна и разметив ее в соответствии с положениями, занимаемыми ползуном.
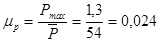
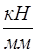
Рассчитываем значения силы Р для каждого положения поршня и заносим в таблицу 1. Для этого определим площадь сечения цилиндра:
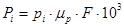 ;
;
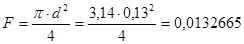 м2
м2
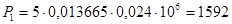 Н
Н
Значение силы Р Таблица1.
| Положения | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Р, Н | 0 | 1592 | 960 | 17246 | 17246 | 3562 | 0 | 0 | 0 |
1.4 Строим планы скоростей для соответствующих положений механизма. На планах изображены векторы скоростей, центров масс и их проекции на направление сил тяжести.
Построение начинаем с входного звена, т.е. с кривошипа ОА. Из произвольно взятой точки Pv , являющейся полюсом плана скоростей, откладываем в направлении движении кривошипа вектор из Pv в точку А, выбранной произвольно.
Выбираем Pv a= 100 мм.
Определяем положение центра масс шатуна
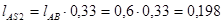 м.
м.
Определяем отрезок на чертеже
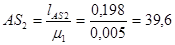 мм
мм
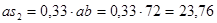 мм,
мм,
где ab – отрезок с плана скоростей , мм.
1.5 Для каждого положения механизма вычислим приведенный момент сил сопротивления 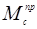 , который определяем по методике [1] стр. 8-9.
, который определяем по методике [1] стр. 8-9.
Используя формулу [1.4] и планы скоростей, определим момент сил для данного механизма.
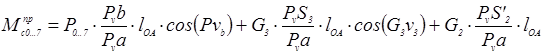 ;
;
Определим массы звеньев:
5 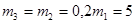 ,5кг
,5кг
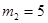 ,5кг;
,5кг;
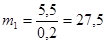 кг.
кг.
Рассчитываем силы тяжести:
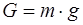 ;
;
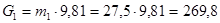 H
H
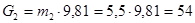 H
H
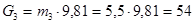 H
H
Определим моменты движущих сил для всех положений момента и заносим результаты в таблицу 2:
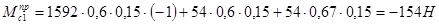
РАЗДЕЛ II
РАЗДЕЛ III
РАЗДЕЛ IV
ЛИТЕРАТУРА
1. Методические указания к выполнению курсового проекта по теории механизмов и машин,− Курган, КМИ, 1984г.
2. Силовой расчёт механизмов. Методические указания к выполнению курсового проекта по теории механизмов и машин, Курган, КМИ, 1992г.
3. Синтез кулачковых механизмов. Методические указания к выполнению курсового проекта по теории механизмов и машин, Курган, КМИ, 1985г.
4. Проектирование эвольвентного зацепления и планетарного механизма с применением ЭВМ. Методические указания к выполнению курсового проекта по теории механизмов и машин, Курган, КМИ, 1989г.
5.Кореняко А.С., Курсовое проектирование по теории механизмов и машин, М.−Л., изд. Машиностроение, 1964г. 324с.
Содержание
Задание для курсового проектирования
Введение - цели и задачи курсового проектирования
1. Синтез и динамический анализ основного механизма
2. Силовой анализ рычажного механизма
3.Проектирование эвольвентного зубчатого зацепления
4. Синтез кулачкового механизма
Литература
Введение
Курсовой проект по дисциплине «Теория механизмов и машин» состоит из графической части и расчетно-пояснительной записки. Включает в себя четыре основных раздела:
1. Синтез и динамический анализ основного механизма.
2. Силовой анализ рычажного механизма.
3. Проектирование эвольвентного зубчатого зацепления и синтез планетарного механизма.
4. Синтез кулачкового механизма.
В первом разделе курсового проекта выполняется проектирования основного рычажного механизма, рассчитывается момент инерции маховика и определяется истинный закон движения звена приведения.
Во втором разделе рассчитываются силы и моменты инерции, приложенные к звеньям, определяются неизвестные реакции в кинематических парах и уравновешивающий момент.
В третьем разделе проводится расчет геометрических параметров, контрольных размеров, качественных и кинематических характеристик эвольвентного зубчатого зацепления. Проводится оценка спроектированной передачи по всем вышеизложенным параметрам. Исходные данные выбираются в соответствии с рекомендациями ГОСТ 16532-70. Здесь же выполняется синтез планетарного механизма.
В четвертом разделе проекта определяются основные параметры кулачкового механизма, и строится профиль кулачка, обеспечивающий заданный закон движения толкателя.
Графическая часть проекта выполняется на четырех листах формата А1 по разделам в соответствии с ГОСТ 2304-68 и ГОСТ 2302-68.
РАЗДЕЛ I
Синтез и динамический анализ основного механизма.
Целью данного раздела является проектирование основного кривошипно-шатунного механизма, определение длин его звеньев, расчет момента инерции маховика, определение истинного закона движения звена приведения.
1.1. По формуле Чебышева определим степень подвижности механизма:
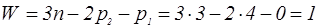
Согласно классификации Артоболевского механизм состоит из: механизма I класса - кривошип ОА, стойка О.
Структурная группа Ассура II класса, II порядка, II вида. - шатун АВ, ползун В; I(0;1) – II2 (2;3) – структурная форма механизма.
В целом механизм является механизмом II класса – по наивысшему.
1.2 По заданным исходным данным спроектируем основной кривошипно-шатунный механизм:
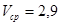 м/с;
м/с;
n1 = 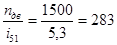 об/мин;
об/мин;
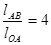
Для этого необходимо определить размеры звеньев, найти положения центров тяжести.
1.2.1. Длину кривошипа lОА вычисляем по формуле:
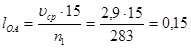 м
м
1.2.2. Определяем длину шатуна:
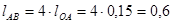 м
м
1.2.3. Определяем масштаб построения:
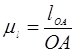 ,
,
где ОА – отрезок произвольно взятый на чертеже, мм.
Принимаем 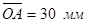
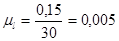
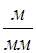
1.2.4. Определяем длину шатуна:
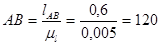 мм
мм
1.2.5.Определим положение центра масс шатуна:
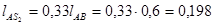 м
м
AS2 = 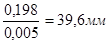
1.3 Вычерчиваем в масштабе диаграмму изменения давления, расположив ось абсцисс параллельно перемещению ползуна и разметив ее в соответствии с положениями, занимаемыми ползуном.
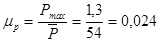
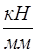
Рассчитываем значения силы Р для каждого положения поршня и заносим в таблицу 1. Для этого определим площадь сечения цилиндра:
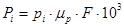 ;
;
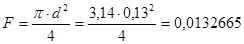 м2
м2
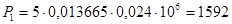 Н
Н
Значение силы Р Таблица1.
| Положения | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Р, Н | 0 | 1592 | 960 | 17246 | 17246 | 3562 | 0 | 0 | 0 |
1.4 Строим планы скоростей для соответствующих положений механизма. На планах изображены векторы скоростей, центров масс и их проекции на направление сил тяжести.
Построение начинаем с входного звена, т.е. с кривошипа ОА. Из произвольно взятой точки Pv , являющейся полюсом плана скоростей, откладываем в направлении движении кривошипа вектор из Pv в точку А, выбранной произвольно.
Выбираем Pv a= 100 мм.
Определяем положение центра масс шатуна
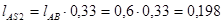 м.
м.
Определяем отрезок на чертеже
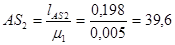 мм
мм
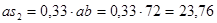 мм,
мм,
где ab – отрезок с плана скоростей , мм.
1.5 Для каждого положения механизма вычислим приведенный момент сил сопротивления 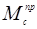 , который определяем по методике [1] стр. 8-9.
, который определяем по методике [1] стр. 8-9.
Используя формулу [1.4] и планы скоростей, определим момент сил для данного механизма.
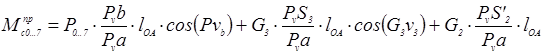 ;
;
Определим массы звеньев:
5 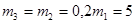 ,5кг
,5кг
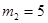 ,5кг;
,5кг;
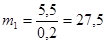 кг.
кг.
Рассчитываем силы тяжести:
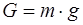 ;
;
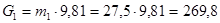 H
H
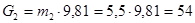 H
H
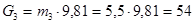 H
H
Определим моменты движущих сил для всех положений момента и заносим результаты в таблицу 2:
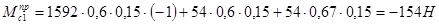
Результаты вычислений приведенного момента сил сопротивления
Таблица 2.
| Положение | 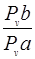
| 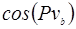
| 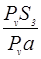
| 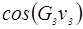
| 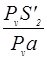
| 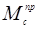 , Н , Н
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,6 | -1 | 0,6 | -1 | 0,67 | -154 |
| 2 | 1 | -1 | 1 | -1 | 0 | -1202 |
| 3 | 0,85 | -1 | 0,85 | -1 | 0,75 | -2212 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0,85 | -1 | 0,85 | -1 | 0,75 | 467 |
| 6 | 1 | -1 | 1 | -1 | 0 | 12 |
| 7 | 0,6 | -1 | 0,6 | -1 | 0,67 | 10,2 |
Строим диаграмму приведенных моментов сил сопротивления в зависимости от угла поворота звена приведения (кривая 1).
Вычисляем масштаб оси абсцисс ():
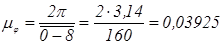 рад/мм
рад/мм
Определяем масштаб диаграммы приведенных моментов сил сопротивления.
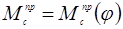
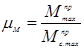 , где
, где
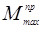 – значение из таблицы 2;
– значение из таблицы 2;
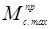 – произвольно принимаем 100 мм.
– произвольно принимаем 100 мм.
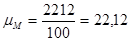
1.6 Вычислим для полученных положений механизма, значения приведенных моментов инерции звеньев и строим диаграмму приведенного момента инерции всех звеньев 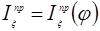 в масштабе:
в масштабе:
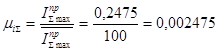
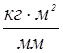
 мм
мм
Приведенный момент инерции 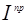 определим из условия равенства его кинетической энергии, суммарной энергии всех подвижных звеньев механизма по методике [1] стр. 9;10;12 используя формулы (17;18;19) можно записать формулу
определим из условия равенства его кинетической энергии, суммарной энергии всех подвижных звеньев механизма по методике [1] стр. 9;10;12 используя формулы (17;18;19) можно записать формулу 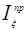 для нашего случая:
для нашего случая:
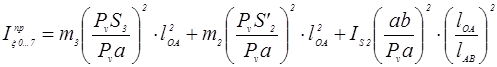 ;
;
Вычислим 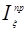 для всех положений и результаты заносим в таблицу 3:
для всех положений и результаты заносим в таблицу 3:
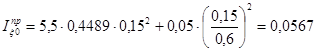
Приведенный момент инерции.
Таблица 3.
| Положение механизма | 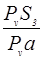
| 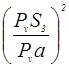
| 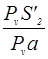
| 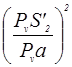
| 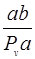
| 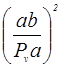
| 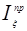 ,
кг·м2 ,
кг·м2
|
| 0 | 0 | 0 | 0,67 | 0,4489 | 1 | 1 | 0,0567 |
| 1 | 0,6 | 0,36 | 0,82 | 0,6724 | 0,7 | 0,49 | 0,129 |
| 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0,2475 |
| 3 | 0,85 | 0,7225 | 0,9 | 0,81 | 0,7 | 0,49 | 0,19 |
| 4 | 0 | 0 | 0,67 | 0,4489 | 1 | 1 | 0,0567 |
| 5 | 0,85 | 0,7225 | 0,9 | 0,81 | 0,7 | 0,49 | 0,19 |
| 6 | 1 | 1 | 1 | 1 | 0 | 0 | 0,2475 |
| 7 | 0,6 | 0,36 | 0,82 | 0,6724 | 0,7 | 0,49 | 0,129 |
1.7 Строим диаграмму избыточных работ 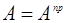 путем интегрирования кривой
путем интегрирования кривой 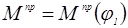 .
.
Масштаб оси ординат диаграммы 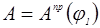 вычисляем по формуле:
вычисляем по формуле:
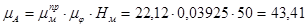 Дж/мм
Дж/мм
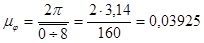
1.8 Строим диаграмму среднего приведенного момента на тех же осях и в том же масштабе 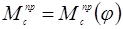 .
.
Величину среднего приведенного момента можно определить графическим дифференцированием графика 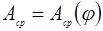 .
.
1.9 Используя уравнение 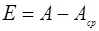
Строим диаграмму изменения запаса кинетической энергии 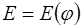 .
.
Определим масштаб оси ординат этой диаграммы:
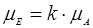 ,
,
где
k – коэффициент пропорциональности, в нашем случае k=1;
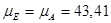 Дж/мм.
Дж/мм.
1.10 Определяем момент инерции дополнительной массы (маховика) обеспечивающий вращение ведущего звена с заданным коэффициентом неравномерности =1/55 и закон его движения.
Динамический синтез механизма проводим методом Виттенбауэра.
Метод Виттенбауэра.
Строим диаграмму «Энергия-масса» путем совместного графического решения двух графиков 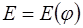 и
и 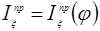 , исключая параметр .
, исключая параметр .
Для удобства построения диаграммы 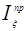 повернем на угол 90°.
повернем на угол 90°.
На диаграмме 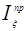 и Е отмечаем соответственно точки 1' и проводим через них горизонтальную и вертикальную линии, на пересечении которой отмечаем точку 1, повторив процедуру получим остальные точки. Полученные точки соединяем плавной линией, строим диаграмму «Энергия-масса».
и Е отмечаем соответственно точки 1' и проводим через них горизонтальную и вертикальную линии, на пересечении которой отмечаем точку 1, повторив процедуру получим остальные точки. Полученные точки соединяем плавной линией, строим диаграмму «Энергия-масса».
1.11 Проведем под углами max и min касательные к кривой «Энергия-масса». Точки пересечения этих касательных с осью ординат обозначаем А и В. Значение tg этих углов вычислим по формулам:

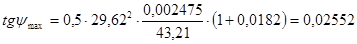
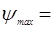 1°27'
1°27'
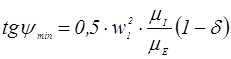
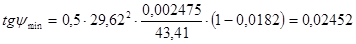
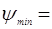 1°24'
1°24'
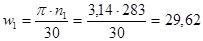 рад/сек
рад/сек
1.12 Определяем момент инерции маховика, обеспечивающий вращения звена приведения с заданным коэффициентом =0,022.
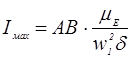 ,
,
где АВ отрезок на оси ординат кривой, «Энергия-масса».
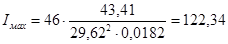 кг м2
кг м2
1.13 Определим значение угловой скорости звена приведения во всех положениях кривошипа, для этого воспользуемся диаграммой «Энергия-масса».
Расчет угловой скорости ведем по формуле:
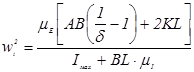 ,
,
где KL – ордината диаграммы «Энергия-масса» в требуемом положении;
BL – абсцисса диаграммы «Энергия-масса» в требуемом положении.
Вычислим угловую скорость для каждого положения:
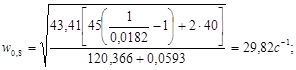
Вычислим изменение угловой скорости для каждого положения:
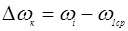
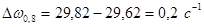
Результаты вычислений угловой скорости заносим в таблицу 4.
Исходные данные и результаты вычислений к ,с-1
Таблица 4.
| Положения маховика | KL | к ,с-1 | ∆к |
| 0 | 40 | 29,82 | 0,2 |
| 1 | 46 | 29,88 | 0,26 |
| 2 | 42 | 29,58 | -0,03 |
| 3 | 18 | 29,54 | -0,077 |
| 4 | 1 | 29,354 | -0,266 |
| 5 | 12 | 29,47 | -0,149 |
| 6 | 24 | 29,60 | -0,02 |
| 7 | 32 | 29,71 | 0,09 |
| 8 | 40 | 29,82 | 0,2 |
По полученным значениям строим график изменения угловой скорости ∆wi= ∆wi(1), относительно прямой, совпадающей со значением угловой скорости звена приведения:
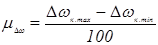
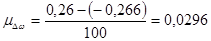
Вывод: входное звено вращается с переменной угловой скоростью и переменным ускорением, за счет действия переменных нагрузок. Т.к. 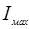 >0, то маховик нужен, чтобы обеспечить заданную неравномерность хода =0,0182.
>0, то маховик нужен, чтобы обеспечить заданную неравномерность хода =0,0182.
РАЗДЕЛ II
Дата: 2019-05-28, просмотров: 268.