2.3.1 Проверочный расчёт передачи на контактную усталость активных поверхностей зубьев выполняем по условию контактной прочности
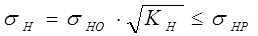
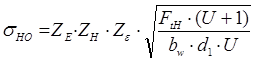
где ZЕ –коэффициент, учитывающий механические свойства сопряженных зубчатых колес;
ZЕ=190[1,с.113];
ZН –коэффициент, учитывающий форму сопряженных поверхностей зубьев в зацеплении;
ZН=2,41 [1,с.113];
Zε –коэффициент, учитывающий суммарную длину контактных линий;
При εβ≥1
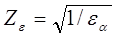[1,с.15]
εα = [1,88 - 3,2 · (1/ Z1 + 1/ Z2)] · cosβ [5,с.39]
εα = [1,88-3,2·(1/26+1/52)]= 1,7
Zε=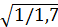 
=0,76
FtH –исходная окружная сила
FtH = 2 · Te1/d1
FtH = 2·26,7·103/53=1007,54 Н
Коэффициент нагрузки Кн определяется по следующей зависимости
Кн = КА· КHv· KHβ· KHα [1,с.14]
где КА –коэффициент, учитывающий внешнюю динамическую нагрузку;
КА =1 [1,с.15];
КHv –коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
V = 0,1· nдв· d1/ 2000
V = 0,1·1430·53/2000=3,78 м/с
При такой скорости следует принять 8 степень точности и тогда:
КHv=1[5,с.40];
KHβ –коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;
KHβ=1,3 [5,с.39];[1,с.58];
KHα –коэффициент, учитывающий распределение нагрузки между зубьями;
KHα =1,09[5,с.39];
КН =1·1·1,03·1,09 =1,12
σно=190·2,41·0,76·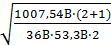 
=308,84МПа
σн = σно·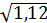 
= 326,84
Определяем процент недогрузки
(σн – σнр)/ σнр · 100%
(326,84-368)/368·100%= 10%
что соответствует рекомендации.
2.3.2 Проверочный расчёт на усталость по напряжениям изгиба выполняем по условию прочности
σF ≤ σFP [1,с.29]
Расчётное местное напряжение при изгибе определяем по формуле:
σF = KF · YFS · Yβ · Yε · FtF /(в · m) [1,с.29]
Для коэффициента нагрузки КF принимают:
КF = КА · КFv · KFβ · KFα [1,с.29]
где КА –коэффициент, учитывающий внешнюю динамическую нагрузку;
КА=1 [1,с.29];
КFv –коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
КFv =1,3[5,с.43];
KFβ –коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
KFβ=1,08[1,с.59];
KFα –коэффициент, учитывающий распределение нагрузки между зубьями.
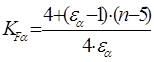5,с.295]
KFα= 
=0,89
YFS –коэффициент, учитывающий форму зуба и концентрацию напряжений, определяется в зависимости от эквивалентного числа зубьев
Zv1 = Z1 / cos3β [1,с.62]
при этом YFs1 =…[1,с.38],[5,с.42].
Zv2 = Z2 /cos3β
при этом YFs2=…[1,с.38],[5,с.42].
Так как шестерня и колесо выполнены из одинаковых материалов, то расчёт ведём по тому из колёс, для которого YFS больше, то есть по шестерне.
Yε –коэффициент, учитывающий перекрытие зубьев:
Yε =1/ εα [1,с.32]
Yβ – коэффициент, учитывающий наклон зуба.
Уβ = 1- εβ · β / 120
εβ = b2 / Рх
Px= Pn / sinβ
Pn= mn· π
Напряжение изгиба σF значительно ниже допускаемого напряжения σFР, но это нельзя рассматривать как недогрузку передачи, поскольку основным критерием её работоспособности является контактная усталость.
Определение геометрических параметров колёс
2.4.1 Высота головки зуба
ha = mn
2.4.2 Высота ножки зуба
hf = 1,25 · mn
2.4.3 Диаметры вершин зубьев
da1 = d1 + 2 · ha
da2 = d2 + 2 · ha
2.4.4 Диаметры впадин зубьев
df1 = d1 - 2 · hf
df2 = d2 - 2 · hf
Дата: 2019-05-28, просмотров: 196.
