Одна из задач уроков трудового обучения — развитие у детей младшего школьного возраста творческого мышления и воображения. В методической литературе приводятся некоторые виды творческих заданий, предлагаемых на уроках труда. Они могут быть связаны, например, с изменением конструкции изделия, а именно: формы, размеров, количества, способов соединения комплектующих деталей; с заменой материалов и с различным оформлением изделия.
В настоящей статье мы хотим рассмотреть задания творческого характера на этапе работы с чертежами и графическими картами, а также предложить в помощь учителю возможные способы разметки к некоторым изделиям.
Обратимся к самому распространенному на уроках труда виду работы с бумагой и картоном — аппликации из геометрических фигур. Эти работы выполняются учащимися начальной школы в разных классах в зависимости от дидактических целей и сложности конструкции изображения.
При изготовлении аппликаций из геометрических фигур у детей совершенствуются навыки разметки, приемы работы с ножницами и клеем; решаются задачи сенсорного развития учащихся, так как, расчленяя сложные фигуры на простые и, наоборот, составляя из простых фигур более сложные, школьники закрепляют и углубляют свои знания о геометрических фигурах, учатся различать их по форме, величине, цвету, пространственному расположению. Кроме того, эти уроки дают возможность знакомить младших школьников с различными техническими объектами (машинами, орудиями труда), их применением в народном хозяйстве, устройством, принципом действия, а также с технической терминологией. Занятия с элементами плоскостного конструирования способствуют в дальнейшем изготовлению объемных моделей технических устройств. Таким образом, эти занятия открывают возможность для развития творческого конструкторского мышления.
Изображения в данном случае носят силуэтный характер. Однако аппликации можно сделать и цветными, если организовать работу в парах, т.е. обменяться какой-либо деталью (деталями) другого цвета с соседом по парте. Возможен и другой вариант — перевернуть деталь неокрашенной стороной (рис. 2).
| Рисунок 1 |
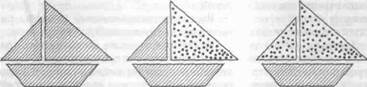
Парусник (рис. 1а) — одна из первых аппликаций из геометрических фигур, которую можно изготовить с первоклассниками, Необходимо организовать деятельность учащихся на уроке таким образом, чтобы она развивала воображение детей. В данном случае у них должен возникнуть образ парусника на основе предложенного графического изображения его деталей.
Для первоклассников эту работу лучше организовать в игровой форме. Учитель может создать ситуацию с любимым героем какой-либо сказки или мультфильма. Например: у Айболита, который в Африке лечит обезьян, кончились лекарства, и ему нужно помочь — отвезти новые.
— Кто помнит, как добирался Айболит до Африки? (Плыл на корабле.)
— Значит, и нам предстоит плыть. Какие средства передвижения по воде вы знаете? (Плот, лодка, корабль, катер, водный велосипед и др.)
— У вас на столах лежат квадраты цветной бумаги, из которых нужно будет построить то, на чем мы поплывем.
— Посмотрите на доску. Какая фигура здесь изображена? (Квадрат.)
— На какие фигуры разделен квадрат? (На два треугольника и четырехугольник.) Это детали будущего изделия.
— Сколько всего геометрических фигур в квадрате, т.е. в заготовке изделия? (Три.) Есть ли одинаковые? Какие? (Треугольники.) Чем они отличаются друг от друга? (Размером.)
— На части какого плавающего средства похожи эти геометрические фигуры? Посмотрите на четырехугольник. Что он вам напоминает? (Лодочку.)
— На что похожи треугольники? (На паруса.)
Далее следует выставить готовый образец аппликации или техникой мокрых деталей собрать на доске изображение парусника (смочить в воде заранее заготовленные детали из бумаги и приклеить на доску.)
— Покажите на аппликации и назовите части парусника. (Корпус, большой парус и маленький парус.) Какую форму они имеют?
— Покажите на рисунке большой парус. Маленький парус. Корпус.
Таким образом, анализ чертежа и соотнесение геометрических форм с частями реальных технических объектов позволили создать образ парусника.
В любой работе учителю важно выделить то главное, что поможет детям воссоздать необходимый образ. В данной работе таким ключевым моментом является вопрос о том, на что похож четырехугольник. При этом существенным может оказаться даже пространственное расположение чертежа, отражающее более или менее естественное положение фигуры в пространстве (четырехугольника) и помогающее увидеть в этой фигуре образ будущего объекта (лодочку).
К тому же оба варианта разметки квадрата могут быть использованы на уроке как задание на развитие воссоздающего воображения. Например: какая лодочка — на берегу, а какая — в море? Почему?
Заготовка деталей аппликации начинается с разметки. Разметка — исходная, основная операция при изготовлении любого изделия. От того, насколько точно и правильно она выполнена, зависит качество работы. При этом нужно отметить, что разметка — одна из сложнейших операций как для учащихся, в силу их возрастных особенностей, так и для учителя, поскольку в литературе, где предлагаются конкретные практические работы, дается только чертеж и в лучшем случае указывается порядок изготовления изделия. А то, каким способом выполнять разметку по данному чертежу, — решать учителю.
Очень важно знать все способы разметки и владеть ими, чтобы выбрать наиболее рациональный, приемлемый, доступный.
Рассмотрим возможные способы разметки деталей аппликации парусника.
Во-первых, можно использовать разметку сгибанием с последующим разрезанием заготовки по линиям сгиба. В I классе, особенно в первом полугодии, дети еще не умеют пользоваться чертежными инструментами и не владеют необходимым математическим материалом. Поэтому разметка сгибанием, где вычерчивание линий заменяется линиями сгибов, часто используется уже в начале учебного года (рис. 2).
| Рисунок 2 |

Однако нужно помнить, что данный прием несколько снизит качество аппликации, так как резать по сгибу неудобно, ровный разрез получить трудно.
Во-вторых, для разметки можно использовать и линейный шаблон (полоску картона нужной ширины). Шаблоном может служить также обычная линейка. В этом случае несколько изменятся пропорции деталей (корпус лодочки уменьшится, т.е. будет уже, а маленький парус соответственно увеличится), но для данной аппликации это несущественно.
В-третьих, разметку можно выполнить и с помощью линейки. Однако для учащихся I класса это будет самый сложный вариант. Разметка диагонали сама по себе не вызовет у детей затруднений, так какне требует разметки точек — достаточно только провести по линейке линию из угла в угол. Сложнее разметить вторую линию, так как нужно найти и отметить точками середину сторон квадрата, а затем по линейке соединить найденные точки. Важно учитывать размер заготовки, чтобы при делении стороны квадрата пополам получилось целое количество сантиметров.
Далее рассмотрим задание творческого характера на примере изготовления аппликации ракеты. В этом случае задание требует от детей деятельности на восстановление недостающих линий чертежа. На начало работы учащимся предлагается образец изделия и неполная схема деления квадрата .
Анализ данного образца и построение чертежа к нему можно организовать следующим образом.
— Ребята, для того чтобы вы смогли собрать такую ракету (показ образца), я сделала на доске чертеж ее деталей. Но злая колдунья Ундина решила вам помешать и испортила его: стерла несколько линий. Перед нами встала задача восстановить их.
Посмотрите на аппликацию. Из каких геометрических фигур построен корпус ракеты? (Из квадрата и прямоугольника.) Покажите их.
— Какую форму имеет нос ракеты? (Форму треугольника.) Ступени? (Тоже треугольники.) Чем они отличаются друг от друга? (Размером.) Сколько всего треугольников использовано в аппликации? (Три.)
— Посмотрите на рисунок, Какую форму имеет заготовка, из которой будем собирать ракету? (Форму квадрата.)
— На какие фигуры разделен квадрат? (На прямоугольники.) Сколько их? (Два.) Сколько прямоугольников нужно для изготовления ракеты? (Один.)
— Значит, из второго прямоугольника мы можем получить недостающие детали. Какие? (Нос, ступени и верхнюю часть корпуса ракеты.) Какую геометрическуюорму они имеют? (Форму квадрата и треугольников.)
— Как получить квадрат (? (Прямоугольник разделить пополам.) Сколько квадратов получилось? (Два.) Сколько нам нужно? (Один.)
— Какой формы детали нам нужно еще заготовить? (Треугольники.) Сколько? (Три.) Какие? (Один большой и два маленьких.)
— Как из второго квадрата разметить треугольники? (Разделить по диагонали.) Сколько треугольников получили? (Два.)
— Какую часть ракеты можем оформить? (Нос.) Что осталось разметить? (Ступени.) Покажите, как вы это сделаете Целесообразно, чтобы всю работу по разметке линий чертежа дети выполняли на доске сами.
Работа по разметке деталей ракеты немного сложнее парусника, так как квадрат нужно разделить на большее количество деталей, но способы разметки аналогичны. Разметка сгибанием.
Порядок разметки и раскроя деталей указан в графической инструкционной карте (рис. 7).
|
|
|
|
2. Разметка с помощью линейного
шаблона.
Если в качестве шаблона, как и в предыдущей работе, использовать линейку, то нужно знать ее ширину. Она может быть 25 мм и 30 мм. При ширине квадрата в 10 см нам нужна узкая линейка (25 мм). Чтобы найти середину стороны заготовки, линейку нужно будет приложить дважды. При разметке первая линия будет вспомогательной, а вторая уже рабочей — линией разреза. Порядок размет
ки и раскроя показан на графической карте.
Если используется другой размер квадрата, то нужно заготовить полоску картона, ширина которой будет равна половине ширины квадрата. При помощи такого линейного шаблона можно будет сразу размечать рабочую линию.
3, Разметка по линейке.
При данном способе порядок разметки фигур сохраняется: прямоугольник, квадрат, треугольники. Сначала удобнее сделать всю разметку, а затем выполнить раскрой деталей. Такая организация работы (когда это возможно) является наиболее целесообразной, так как повторение одинаковых операций (сначала разметка по линейке, а затем разрезание ножницами) больше способствует формированию трудовых умений. Кроме того, это позволяет экономить время на уроке.
Итак, мы рассмотрели задания творческого характера на этапе работы с чертежами и графическими картами, а также предложили возможные способы разметки на примере лишь двух аппликаций из квадратов цветной бумаги. Однако существует много работ подобного типа.
Заключение
Главный принцип формирования мышления учащихся—системность. Все основные компоненты мыслительного развития (целевой, содержательный, операционный, мотивационный и контрольно-коррекционный) неразрывно связаны между собой: знания—основа мыслительного развития; чем целесообразнее способы добывания знаний, тем они полноценнее; учение с интересом, с увлечением активизирует процесс мышления, воспитания положительных качеств личности. Если, пользуясь аналогией, целенаправленно добытые знания можно представить в виде фундамента здания, то способы мыслительной деятельности — это орудия труда, а мотивы деятельности — это энергия, которая движет строителями. Н если в данной системе не будет какого-то компонента, то не будет и «здания».
Ведущая роль в умственном развитии принадлежит содержанию образования, системе научных знаний, которыми овладевают учащиеся. Поэтому, предлагая детям ту или иную задачу, мы прежде всего учитываем наличие знаний по данному вопросу, так как знаем, что «пустая голова не рассуждает» (П. П. Блонский). И вместе с тем бывает, что ученик десять лет лихорадочно заполнял «емкости» своей памяти самой разнообразной информацией, а самостоятельно применять знания не умеет. По выражению академика А. Л. Минца, такой человек напоминает фаршированную рыбу, которая плавать неспособна.
Известно, что если у ребенка нет желания учиться, отсутствует интерес к знаниям, к способам их освоения, то и нет надежды воспитать из него человека-творца. Вот почему содержательная сторона обучения, являясь ведущей, не должна умалять роли мотивационной и операционной сторон. Поэтому не случайно, как подчеркивал П. П. Блонский, развитое мышление проявляет себя в рациональных способах запоминания и припоминания. И только низким уровнем развития мышления, его операционных структур можно объяснить те случаи, когда ученики заучили материал, но не умеют выделить в нем главное, сопоставить факты, явления, обобщить, доказать свою мысль и т. п. Наряду с этим нельзя развивать мышление вне мотивацнонного аспекта. С какой целью, для чего учится школьник? С каким настроением? Каковы мотивы и потребности учащегося? Все это есть своеобразный движитель мысли, ее пытливости, глубины, широты и т. п. В этой связи следует заметить, что принцип сознательности в обучении иногда трактуется упрощенно: понимают учащиеся материал, уверенно отвечают на вопросы учителя,—значит, и усваивают сознательно. Истинная же сознательность заключается в том, что ученик убежден, знает, почему ему необходимо учиться, зачем нужны те или иные знания, умения, навыки, как и где применить.
Школьник учится, думая и думает, учась: там, где нужно найти ответ на вопрос, что-то понять, и начинается мышление. Однако думает, мыслит каждый ученик по-своему. Поэтому, изучая характер мышления ученика, важно выяснить, как он преимущественно мыслит: понятиями или образами? Известно, что И. П. Павлов на этой основе различал «мыслителей», «художников» и смешанный тип людей. На практике нетрудно и среди учащихся отличить «мыслителя» от «художника» по приемам его работы. Например, составляя план, ученики с развитым понятийным мышлением кратко, обобщенно формулируют пункты, делают пометки в виде вопросов, выводов и др. Ученики с образным типом мышления делают план в рисунках, цитатный план. При этом надо учитывать, что развитие мышления школьников в возрастном аспекте осуществляется от наглядно-действенного в дошкольном возрасте к образно-речевому в младшем и к понятийному, теоретическому в среднем и старшем школьных возрастах. Конечно, границы эти подвижны, динамичны; многое тут зависит от характера и качества процесса обучения, которое «ведет за собой развитие». Данное положение Л. С. Выготского имеет методологическое значение для понимания детского мышления.
Таким образом, учить мыслить школьников в процессе обучения—это значит, учитывая их природные особенности, опираться на методологические и психологические основы их развития, обеспечивать усвоение содержания учебных предметов при одновременном учете операционного и мотивационного аспектов учения.
Литература
1. Выбор методов обучения в средней школе.-М.,1981
2. Дусавицкий.А.К .2*2=?.-М.,1995
3. Еремеева.О.О.Один из приемов поиска решения задач.//Начальная школа.-№7.-2003.-с.43
4. ЗанковМ.И.Обучение и развитие.-М.,1975
5. Лук.А.Н.Мышление и творчество.- М.,1976
6. Паламарчук В.Ф. Школа учит мыслить. – М.,1987
7. Пономерев.Я.А.Знания, мышления и умственное развитие.-М.,1967
8. Пономарев.Я.А.-Психология творческого мышления.-М.,1960
9. Развитие творческой активности школьника. – М.,1991
10. РубинштейнС.Л.О мышлении и путях его исследования.-М,1958
11. СуриковаМ.В.Задания творческого характера//Начальная школа.-№12.-1997.-с.51
Приложение
Задание 1.
На рассмотроение слов по одному общему признаку: по буквам. обозначающим гласные звуки.
Сон, сын, сад, рот, рак, дом, дым, дал, вол, выл, вал, рыл.
Устно дается инструкция; "Прочитайте слова. На какие три равные группы можно разделить эти слова?"
Целью данного задания является привлечение учащихся к обдумыванию, сравнению слов, рассуждению, высказыванию собственного суждения. Данное задание дает простор мысли ученика. Первые же слова сон-сын наблюдательных детей приведут к выводу: слова различаются буквами, обозначающими гласные звуки. Если этот признак будет распространен на все остальные слова, последует вывод, что в словах встречаются все три буквы, обозначающие гласные звуки: о, ы, а, и в каждой группе должны быть слова с одной из этих букв.
сон сын сад
рот рыл рак
дом дым дал
вал выл вал
Другие дети могут зафиксировать различия слов по их значениям. Допустим, дети разделят так:
1) одушевленные - сын, рак, вол (само понятие одушевленности им еще неизвестно, но интуитивно дети могут выделить признак "живые";
2) неодушевленные (неживые) - сон, сад, рот, дом, дым, вал.
3) "что-то делают" - рыл, дал, выл.
Во всех этих случаях получается неравное количество слов, что противоречит условию задания. Может возникнуть и предложение разделить слова по начальным или конечным согласным. Но разных согласных больше, чем три, следовательно, искомых трех групп тоже не получится.
Путем коллективного обсуждения, привлечения всех учашихся к участию в выполнении задания, оно будет выполнено. В заключение учитель дает задание записать каждую группу слов в отдельный столбик.
Дата: 2019-05-28, просмотров: 337.

