Свободная длина элемента верхнего пояса фермы при расчете в плоскости фермы при е0 = 0,031 < h / 8 = 0,025 равна l0 = 0.9l = 0.9·3=2,7 м [2, табл.33].
Вычисляем случайные эксцентриситеты:
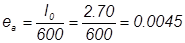 м ,
м , 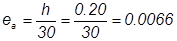 м.
м.
Принимаем наибольшее значение: eo = 0.031 м.
кНм.
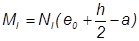 = 664··(0.031 + 0.01 – 0.04) = 60,42 кНм
= 664··(0.031 + 0.01 – 0.04) = 60,42 кНм
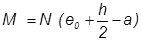 = 817.695·(0.031 + 0.1 – 0.04) = 74.4 кНм
= 817.695·(0.031 + 0.1 – 0.04) = 74.4 кНм
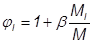 =
= 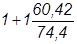 =1.812;
=1.812;
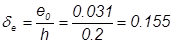 , но не менее:
, но не менее:
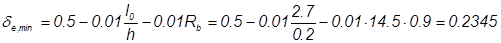 ,
,
принимаем δe = 0,2345;
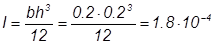 м-4;
м-4;
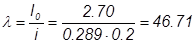 , откуда
, откуда 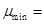 0,2% [3, табл. 38];
0,2% [3, табл. 38];
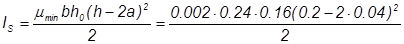 = 0.023·10-4 м-4;
= 0.023·10-4 м-4;
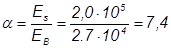
Критическая сила при потере устойчивости:
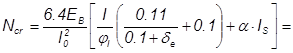
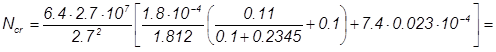 1413 кН
1413 кН
Коэффициент продольного изгиба:
5.3.2. Определение сечения арматуры при симметричном армировании
Эксцентриситет с учетом продольного изгиба:
е0·η = 0,031·2,374 = 0,0725м, что больше 0,3h = 0.3·0.2 = 0.06м
Предварительно принимаем случай “больших” эксцентриситетов.
1. Задаем сечение арматуры (4 Æ20 с AS = A’S=12.56см2) [1, прил.3].
2. Определяем 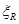 (граничную высоту сечения).
(граничную высоту сечения).
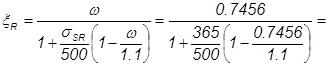 0,605 [3, (25)],
0,605 [3, (25)],
где ω =0,85 – 0,08·RB = 0.85 – 0.08·17·0.9 = 0.7456 [3, (26)]
для арматуры A-IV: σSR = RSC + 400 - σSP - ΔσSP = 510 + 400 = 910МПа,
σSP = 0, ΔσSP =0, тк. отсутствует предварительное напряжение.
3. Определим требуемую относительную высоту сжатой зоны сечения:
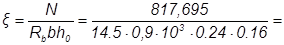 1,47 > 0.605
1,47 > 0.605
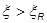 - случай “малых” эксцентриситетов.
- случай “малых” эксцентриситетов.
Определим требуемую относительную высоту сжатой зоны сечения для случая “малых” эксцентриситетов:
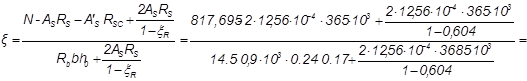 0,651
0,651
4. Определяем
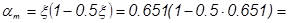 0,439
0,439
5. Проверяем несущую способность по формуле:

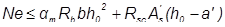 [3, (36)],
[3, (36)],
где:
Ne =N 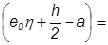 817.695·(0,031·2,374 + 0.2/2 – 0.03)=117.42 кНм
817.695·(0,031·2,374 + 0.2/2 – 0.03)=117.42 кНм
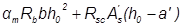 =
=
=0,439·0,24·0,172·14,5·103·0,9 + 365·103· 12.56·10-4·(0,17-0,03) =104Нм
 Условие не выполняется 117,42кНм>104кНм.
Условие не выполняется 117,42кНм>104кНм.
Увеличим сечение арматуры, принимаем (4 Æ20 с AS = A’S=15,2см2)
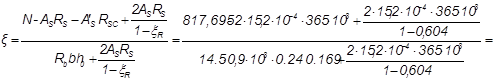 0,754
0,754
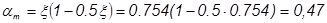
Ne =N 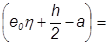 817.695·(0,031·2,374 + 0.2/2 – 0.031)=116,6 кНм
817.695·(0,031·2,374 + 0.2/2 – 0.031)=116,6 кНм
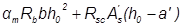 =
=
=0,47·0,24·0,1692·14,5·103·0,9 + 365·103· 12.56·10-4·(0,169-0,031) =118,6Нм
116,6 кНм <118,6Нм
Условие [3, (36)] выполняется. Сечение показано на рисунке 5.2.
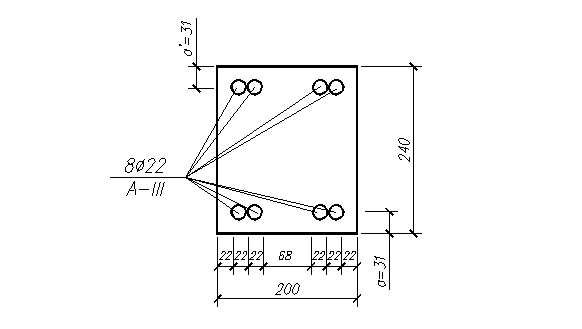 Рис. 5.2 – Сечение верхнего пояса.
Рис. 5.2 – Сечение верхнего пояса.
Назначение поперечной арматуры
Согласно [3, п.5.22] принимаем поперечную арматуру с шагом 400, что меньше 20d = 20  22 = 440 и 500 мм. Диаметр арматуры назначаем из условия свариваемости [4, прил.9] и наличия в сортаменте. Принимаем ø6AIII.
22 = 440 и 500 мм. Диаметр арматуры назначаем из условия свариваемости [4, прил.9] и наличия в сортаменте. Принимаем ø6AIII.
Расчет нижнего пояса
Исходные данные:
Класс бетона: В25, Rb =14,5 МПа; γb2=0.9, EB = 27000 МПа.,
Rb,ser = 18,5 МПа, Rbt,ser 1,6 МПа;
Класс арматуры A-IV; Rs = 510 МПа; Rsc = 450 МПа; Rs,ser =590МПа;
ES = 19000МПа
Сечение 24´22см.
Расчетные усилия: М = - 32,63 кНм, N = 776,7 кН.
a=a’=0,05 м.
Определение сечения арматуры
Армирование симметричное AS = A’S
Эксцентриситет силы N (рис. 5.3):
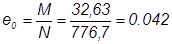 м;
м;
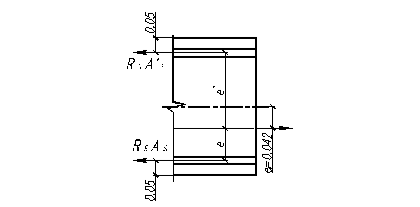
Рис.5.3 - Расчетная схема нижнего пояса.
Так как е0 < 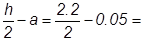 0,06 м, то сила N находится между арматурами и это случай “малых” эксцентриситетов, расчет ведется по формулам:
0,06 м, то сила N находится между арматурами и это случай “малых” эксцентриситетов, расчет ведется по формулам:
Ne ≤ A’SRS(h0-a’) [3, (61)]
Ne’ ≤ ASRS(h0-a’) [3, (62)]
При симметричном армировании получим:
е0 = 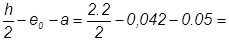 0.018м;
0.018м;
е’ = 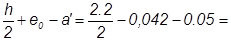 0.102м.
0.102м.
Выбираем большее значение и получим:
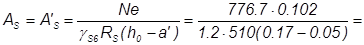 10.6·10-4м2
10.6·10-4м2
где γS6 = η =1.2 для арматуры класса A-IV [3, п.3.13].
Принимаем 3Æ22 AS = A’S = 11,4м2 [1, прил.3].
Суммарная арматура: AS + A’S = 22,8 м2.
Процент армирования сечения:
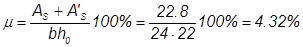
Проверка размещения стержней в сечении:
b > 3·2,2 + 2·5 + 2·2,5 = 21см.
Размещение стержней показано на рисунке 5.4.
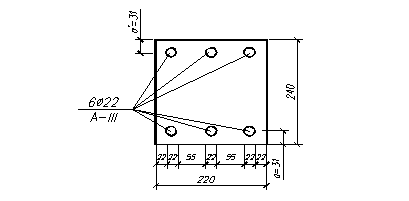
Рис. 5.4 – Размещение продольной напрягаемой арматуры.
5.4.2. Назначение предварительного напряжения
В соответствии с [3, п. 123] должны удовлетворяться условия:
σsp + p ≤ Rs,ser; σsp - p ≥ 0.3Rs,ser; [3, (1)]
Величина р при механическом способе натяжения арматуры принимается равной p = 0.05σsp [2, п.1,23], тогда:
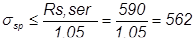
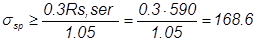 МПа.
МПа.
Назначаем σsp = 550МПа.
5.4.3. Потери предварительного напряжения
Натяжение арматуры производится на упоры [по заданию].
Первые потери
1) От релаксации напряжения при механическом способе натяжения стержневой арматуры:
σ 1 = 0.1σsp -20 = 55 – 20 = 35МПа;
2) От перепада температур для бетона В25:
σ 1 = 1.25Δt = 1.25·65 =81МПа;
3) От деформации анкеров:
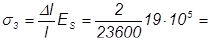 16МПа;
16МПа;
4) От позиции 4 [3, табл.5] потерь нет (натяжение на упоры);
5) От позиции 5 [3, табл.5] потерь нет (стержневая арматура);
6) Потери от быстро натекающей ползучести 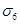 :
:
Усилие в арматуре с учетом потерь (позиции 1 – 5):
P1 = [σ – (σ1+σ2+σ3)]Asp = [550 – (35+81+16,1)]22,8·10-4·103 = 953 кН;
Сжимающие напряжения в бетоне от силы Р1:
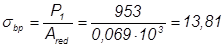
где Ared = Ab + αAS = 0.24·0.22 + 7.04·22.8·10-4 = 0.069 м2
Передаточная прочность бетона принимается по [3, п.2.6].
Для арматуры класса А-IV:
Rbp ≥ 11МПа кроме того, Rbp ≥ 0,5B = 0,5·25 =12,5МПа.
Принимаем Rbp =12,5МПа;
α=0,25+0,025Rbp =0.25+0.025·12.5 =0.563 < 0.8;
β=5.25-0.185 Rbp = 5.25 – 0.185·12.5 = 2.94 (но не более 2.5), принимаем β=2,5;
Т.к. 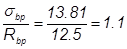 > α, то
> α, то
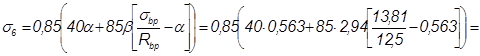 117МПа
117МПа
Суммируем, первые потери напряжений:
σlos1 = 35+81+16+0+0+117 = 249МПа
Усилие в арматуре с учетом первых потерь:
P1 = (σsp –σlos1 )As = (550 – 249)22.8·10-4·103 = 682.3кН.
Вторые потери
7) Потери релаксации напряжений арматуры учтены в 1) пункте;
8) Потери напряжений от усадки бетона при классе бетона В25 и тепловой обработке σ8=35 МПа.
9) Ползучесть бетона:
Сжимающие напряжения в бетоне с учетом первых потерь:
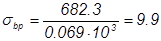 МПа. Так как
МПа. Так как 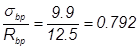 >0.75, то:
>0.75, то:
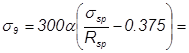 106МПа.
106МПа.
α = 0,85 –коэффициент принимаемый для бетона подвергнутого тепловой обработке при атмосферном давлении.
Полные потери:
σlos = σlos1 + σlos2 = 249+(35+106) = 390МПа
МПа 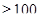 МПа.
МПа.
Усилие предварительного обжатия с учетом полных потерь напряжений:
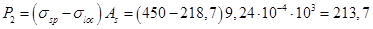 кН.
кН.
5.4.4. Расчет по образованию трещин
Средний коэффициент надежности по нагрузке определяем по [табл.2.1] с учетом снеговой нагрузки:
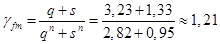 ;
;
Нормативные усилия равны (первая панель нижнего пояса):
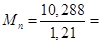 8,502 кНм;
8,502 кНм;
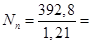 324,6 кН.
324,6 кН.
Нормативные усилия от длительных нагрузок (см. раздел п.5.3):
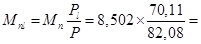 7,262 кНм;
7,262 кНм;
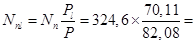 277,3 кН.
277,3 кН.
Проверка по образованию трещин производится по формуле
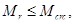 [3, (124)]
[3, (124)]
где 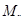 - момент от внешних сил относительно оси параллельной нулевой линии и проходящей через ядровую точку наиболее удаленную от растянутой зоны, трещиностойкость которой проверяется:
- момент от внешних сил относительно оси параллельной нулевой линии и проходящей через ядровую точку наиболее удаленную от растянутой зоны, трещиностойкость которой проверяется:
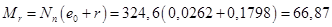 кНм;
кНм;
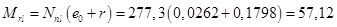 кНм,
кНм,
где 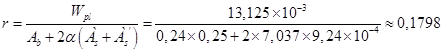 м,
м,
где 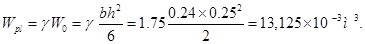
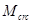 - момент, воспринимаемый сечением при образовании трещин.
- момент, воспринимаемый сечением при образовании трещин.
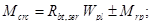 [3, (125)]
[3, (125)]
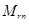 - ядровый момент от силы
- ядровый момент от силы 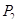 .
.
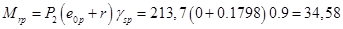 кНм [3, (129)]
кНм [3, (129)]
где 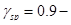 коэффициент точности натяжения арматуры при механическом способе натяжения [3, п.1.27].
коэффициент точности натяжения арматуры при механическом способе натяжения [3, п.1.27].
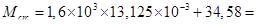 55,58 кНм.
55,58 кНм.
Так как при полном загружении нормативной нагрузкой условие [3, (124)] не выполняется ( 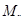 = 66,87 >
= 66,87 > 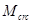 = 55,58), а так же при действии длительной части нагрузки условие [3, (124)] не выполняется (
= 55,58), а так же при действии длительной части нагрузки условие [3, (124)] не выполняется ( 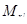 = 57,12 >
= 57,12 > 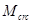 = 55,58), трещины образуются и необходимо проверить их раскрытие.
= 55,58), трещины образуются и необходимо проверить их раскрытие.
Расчет на раскрытие трещин
Ферма находится в закрытом помещении и поэтому относится к 3-ей категории трещиностойкости, для которой допускается ограниченное по ширине непродолжительное ( 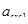 =0,4 мм) и продолжительное (
=0,4 мм) и продолжительное ( 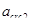 =0,3 мм) раскрытие трещин [3, п.1.16, табл.2].
=0,3 мм) раскрытие трещин [3, п.1.16, табл.2].
Раскрытие трещин определяется по формуле:
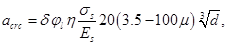 [3, (144)]
[3, (144)]
где 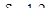 для внецентренно растянутых элементов;
для внецентренно растянутых элементов; 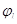 - коэффициент длительности действия нагрузки. Для непродолжительного действия нагрузки
- коэффициент длительности действия нагрузки. Для непродолжительного действия нагрузки 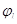 =1. Для тяжёлого бетона естественной влажности при длительном действии нагрузки
=1. Для тяжёлого бетона естественной влажности при длительном действии нагрузки 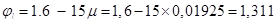 , где
, где 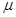 - коэффициент армирования сечения:
- коэффициент армирования сечения: 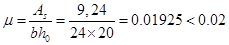 ;
; 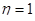 - для стержневой арматуры периодического профиля; d=14 - диаметр арматуры в мм;
- для стержневой арматуры периодического профиля; d=14 - диаметр арматуры в мм; 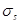 - приращение напряжений в арматуре от действия внешней нагрузки [3, п.4.15].
- приращение напряжений в арматуре от действия внешней нагрузки [3, п.4.15].
1. Определяем раскрытие трещин от кратковременного действия всех нагрузок 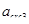 . Эксцентриситет равнодействующей продольных сил
. Эксцентриситет равнодействующей продольных сил 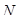 и
и 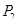 относительно центра тяжести сечения равен:
относительно центра тяжести сечения равен:
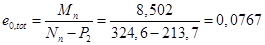 м
м 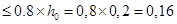 м.
м.
Т.к. 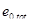
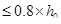 то можно в формуле [3, (148)] принять
то можно в формуле [3, (148)] принять 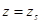 (
( 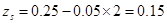 м расстояние между арматурой
м расстояние между арматурой  и
и  ).
).
Тогда напряжение в арматуре:
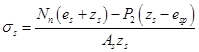 [3, (148)]
[3, (148)]
где 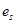 - эксцентриситет силы
- эксцентриситет силы 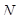 относительно арматуры
относительно арматуры 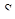 (рис. 5.5)
(рис. 5.5)
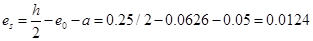 м
м
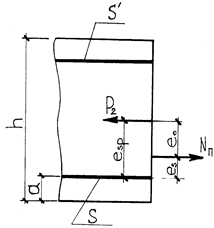
Рис.5.5 - Приложение силы преднапряжения.
Эксцентриситет силы 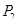 относительно арматуры
относительно арматуры 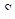 :
:
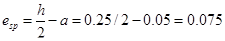 м.
м.
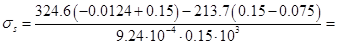 206,6 МПа [3, (148)];
206,6 МПа [3, (148)];
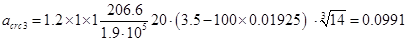 мм [3, (144)];
мм [3, (144)];
2. Определяем  - раскрытие трещин от кратковременного действия постоянной и длительной нагрузки при
- раскрытие трещин от кратковременного действия постоянной и длительной нагрузки при 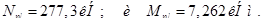
Так как 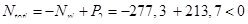 сечение растянуто.
сечение растянуто.
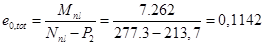 м
м 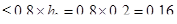 м.
м.
Т.к. 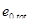
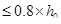 то можно в формуле [3, (148)] принять
то можно в формуле [3, (148)] принять 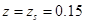 м.
м.
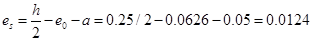 м
м
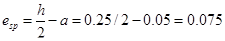 м.
м.
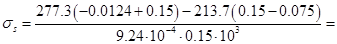 159,7 МПа [3, (148)];
159,7 МПа [3, (148)];
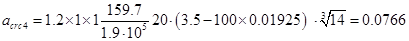 мм [3, (144)];
мм [3, (144)];
3. Определяем 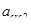 - продолжительное раскрытие трещин (от постоянной и длительной нагрузки) при
- продолжительное раскрытие трещин (от постоянной и длительной нагрузки) при 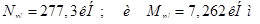 и
и 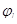 =1,311:
=1,311:
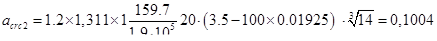 мм [3, (144)];
мм [3, (144)];
Непродолжительное раскрытие трещин равно:
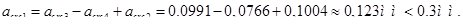
Полученные значения раскрытия трещин 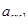 и
и 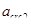 не превышают предельных величин, установленных нормами проектирования.
не превышают предельных величин, установленных нормами проектирования.
Дата: 2019-05-28, просмотров: 352.