Важливим показником експлуатаційної роботи залізничної ділянки є пропускна спроможність, визначувана мінімальним, таким, що реалізовується при відповідній системі забезпечення безпеки руху (СЗБР) інтервалом попутного проходження потягів. Методика розрахунку даного інтервалу для різних елементів залізничної ділянки при існуючих СЗБР викладена в спеціальних інструкціях. Проте доцільно оцінити величину мінімального інтервалу попутного проходження потягів, що реалізовується, забезпечуваної при устаткуванні ділянки деякій ідеальною СЗБР, в якій управління поїздом здійснюється на підставі отримання в кожній точці шляху у будь-який момент часу точної інформації про координату, швидкість проходження і шляху екстреного гальмування складу, що йде попереду. Розрахована для ідеальної системи величина інтервалу міжпотягу, а отже, і пропускна спроможність, що потенційно реалізовується, є еталоном при оцінці експлуатаційних показників залізничної ділянки і якості управління в тих, що існують і СЗБР, що розробляються. Завданню визначення інтервалу міжпотягу, що потенційно реалізовується, для різних елементів залізничної ділянки присвячені роботи [1...3]. У даній роботі вирішення вказаної задачі, а також оцінку пропускної спроможності, що потенційно реалізовується, в різних точках залізничної ділянки пропонується здійснювати з використанням спеціальних математичних моделей.
При організації безупинного руху потягів через довільно узяту точку залізничної ділянки можна розглядати як формування в ній послідовності імпульсів з тривалістю Тп, визначуваною довжиною складу l і швидкістю V його проходження.
Період проходження імпульсів обернено пропорційний середньому значенню швидкості складу на даному інтервалі:
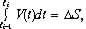 (3)
(3)
При устаткуванні ділянки ідеальної СЗБР, що передбачає управління по координаті кінця потягу, що йде попереду, і використання рівносповільненої моделі службового гальмування, мінімальна можлива відстань між двома поїздами може бути обчислено за формулою:
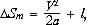 (4)
(4)
де а — розрахункова величина уповільнення складу на даній ділянці.
Процес формування імпульсів при постійній швидкості V руху потягів по даній ділянці може бути описаний математичною моделлю, представленою на мал. 1, розробленій на основі моделі частотно-імпульсної модуляції [4]. Нелінійний елемент забезпечує задання швидкості потягу залежно від відстані _Sm до кінця поїзду, що йде попереду. При досягненні параметром S значення _Sm виробляється d-функція, використовувана для формування лінійною ланкою прямокутного імпульсу і скидання інтегратора в нуль. Збільшенню швидкості руху на ділянці обов'язково повинне передувати збільшення відстані між поїздами _Sm.
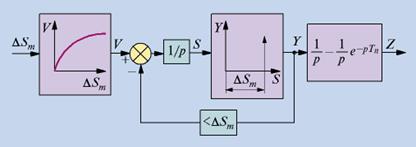
Рис.14 Математична модель, що описує рух потягів з постійною швидкістю і міжпоїздовим інтервалом, що потенційно реалізовується, по ділянці, обладнаній ідеальною СЗБР
Розрахункова довжина і довжина, що реалізовується в режимі службового гальмування уповільнення потягів визначаються характеристиками залізничної ділянки і рухомого складу, що рухається на нім. Тому доцільно досліджувати залежність що потенційно реалізовується при ідеальній СЗБР інтервалу міжпотягу від встановленої швидкості руху на ділянці. Використання рівносповільненої моделі службового гальмування дозволяє записати:
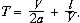 (5)
(5)
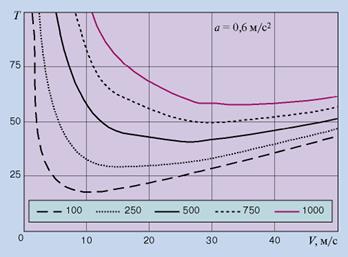
Рис.14 Залежність інтервалу між потягу, що потенційно реалізовується, від швидкості руху потягів по ділянці, обладнаній ідеальною СЗБР
Досліджуючи функцію на екстремум, досягнемо значення швидкості
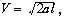
при якому забезпечується мінімальне, рівне 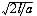 значення інтервалу міжпотягу. Залежність даного інтервалу від швидкості руху на ділянці при різних розрахункових значеннях довжини і уповільнення складів ілюструє Рис.14. Тут же в таблиці (див. мал. 2) приведені значення що потенційно реалізовуються в точках екстремуму функції інтервалу міжпотягу Tmin, а також відповідні кожній точці значення швидкості Vэкст і довжини l складу.
значення інтервалу міжпотягу. Залежність даного інтервалу від швидкості руху на ділянці при різних розрахункових значеннях довжини і уповільнення складів ілюструє Рис.14. Тут же в таблиці (див. мал. 2) приведені значення що потенційно реалізовуються в точках екстремуму функції інтервалу міжпотягу Tmin, а також відповідні кожній точці значення швидкості Vэкст і довжини l складу.
| l, м | 100 | 250 | 500 | 750 | 1000 |
| Vэкст, м/с | 10,95 | 17,32 | 24,5 | 30 | 34,64 |
| Tmin, с | 18,26 | 28,87 | 40,82 | 50 | 57,74 |
Для оцінки що реалізовується в умовах ідеальної СЗБР інтервалу входу на станцію або ділянку обмеження швидкості передбачається використовувати математичну модель, представлену на мал. 3. Завдання закону зміни швидкості потягу на підході до ділянки її обмеження а або станції б здійснюється за допомогою вхідних до складу моделі нелінійних елементів 1, 2. Елемент 1 відтворює закон зміни швидкості V0, реалізація якого забезпечує проходження складів з мінімально можливим в даному випадку міжпоїздовим інтервалом [1...3]. Елемент 2 визначає зміну швидкості Vи, що реалізовується при досліджуваному процесі управління веденням потягу. Елементи 3, 4 забезпечують ухвалення параметром V значення Vи або V0, що обирається з урахуванням співвідношення швидкостей, що задаються. Призначення елементів 5...7 ідентично призначенню вже розглянутих вище аналогічних функціональних елементів, що входять до складу моделі, представленої на Рис.13.
Дата: 2019-05-28, просмотров: 318.