Вступ
Математична модель в механіці - це замкнута система математичних співвідношень, що дозволяє з прийнятною точністю вивчати особливості поведінки даного об'єкту, що цікавлять дослідника.
Математичне моделювання в механіці керованих систем має ряд особливостей:
· Що вивчаються в механіці керованого руху об'єкти надзвичайно різноманітні. Автомобіль, гіроскопічний стабілізатор, крокуючий робот, імітатор космічного польоту і т.п. складаються з різних жорстких конструктивних елементів, пристроїв, датчиків, двигунів. З теоретико-механічної точки зору всі ці об'єкти можуть розглядатися як системи, що складаються з великого числа взаємодіючих твердих тіл. Спроба скласти математичну модель такого об'єкту за допомогою класичних методів теоретичної механіки, наприклад у формі рівнянь Лагранжа, зазвичай приводить до неймовірно громіздких рівнянь, що налічують сотні і тисячі доданків. Виникає потреба в наближеному моделюванні, яке для чітко обумовленого класу руху описує потрібні явища з прийнятною точністю.
· Для систем, керованих рухів, що вивчаються механікою, характерні сильні загасання високочастотних власних складових руху. Наближене моделювання таких систем тяжіє до побудови розкладань А. Пуанкаре і погрансольним методам А.Н. Тихонова - А.Б. Васильєвої.
Проникнення математичних методів в найрізноманітніші, часом несподівані сфери людської діяльності означає можливість користуватися новими, як правило, вельми плідними засобами дослідження. Зростання математичної культури фахівців у відповідних областях призводить до того, що вивчення загальних теоретичних положень і методів обчислень вже не становить серйозних труднощів. Але на практиці виявляється, що одних лише математичних пізнань далеко не достатньо для вирішення того або іншого прикладного завдання необхідно ще отримати навики в перекладі початкового формулювання завдання математичною мовою.
Ситуації моделюють для різних цілей. Головна з них необхідність передбачати нові результати або нові властивості явища. Ці прогнози можуть бути пов'язані з розповсюдженням існуючих результатів або мати принциповіший характер. Часто вони відносяться до умов, які, ймовірно, матимуть місце в деякий момент в майбутньому. З іншого боку, прогнози можуть відноситься до подій, безпосереднє експериментальне дослідження яких нездійсненно. Найбільш важливий приклад такого роду дають численні прогнози, які робилися на основі математичних моделей в програмі космічних досліджень. Проте для цієї мети моделюються не всі ситуації: в деяких випадках досить вміти описувати математичними засобами роботу системи для того, щоб добитися глибшого розуміння явища (саме цю роль і грають багато видатних фізичних теорій, хоча на їх основі робляться також і прогнози). Зазвичай при такому математичному описі не враховується елемент контролю, проте в моделях, побудованих, наприклад, для дослідження роботи мереж, таких як схеми руху потягів або літаків, контроль часто є важливим чинником.
Математична модель є спрощенням реальної ситуації. Відчутне спрощення наступає тоді, коли неістотні особливості ситуації відкидаються і складне початкове завдання зводиться до завдання, що ідеалізується, піддається математичному аналізу. Саме при такому підході в класичній прикладній механіці виникли блоки без тертя, невагомі нерозтяжні нитки, нев'язкі рідини, абсолютно тверді або чорні тіла і інші подібні моделі, що ідеалізуються. Ці поняття не існують в реальній дійсності, вони є абстракціями, складовою частиною ідеалізації, зробленій автором моделі. І проте їх часто можна з успіхом вважати хорошим наближенням до реальних ситуацій. Описаний образ дій при побудові математичних моделей не є єдиним, і цьому зовсім не варто дивуватися. У іншому можливому підході першим кроком є побудова простій моделі декількох найбільш характерних особливостей явища. Це часто робиться для того, щоб відчути дане завдання, причому робиться це ще до того, як саме завдання остаточно сформульоване. Потім ця модель узагальнюється, щоб охопити інші факти, поки не буде знайдено прийнятне або адекватне рішення. Є ще підхід, коли із самого початку вводиться в розгляд одночасне велике число чинників. Він часто застосовується в дослідженні операцій, і такі моделі зазвичай вивчають імітаційними методами з використанням ЕОМ.
Актуальність теми. Одна з основних проблем сучасного локомотивобудування - забезпечення високих тягових і динамічних характеристик локомотивів, які в основному визначаються конструкцією екіпажної частини і технічним станом системи колесо - рейка.
У останні десятиліття з метою зменшення силової взаємодії і зносу гребенів коліс і рейок в кривих велася цілеспрямована і системна робота по впровадженню нових профілів коліс і технологій змазування гребенів і рейок. Це значно понизило гостроту проблеми виходу з експлуатації рейок і бандажів локомотивних коліс внаслідок підвищеного зносу. В той же час збільшилася контактно-втомна пошкоджуваність коліс і рейок.
Дослідження динаміки локомотивів і зношування гребенів в більшості теоретичних і експериментальних робіт виконувалися на вибігу, а не під тягою, при контакті нових коліс, у тому числі і з криволінійним профілем, з новими або мало зношеними рейками і без змазування.
Вивчення динаміки з погляду силової взаємодії і зношування гребенів коліс локомотива в режимах вибігу і тяга при різному технічному стані системи колесо - рейка є актуальним завданням.
Елементи залізниці
Рейка. Майже всі рейки в поперечному перетині мають тавровий (Т-образний) профіль з плоскою підставою, вузькою вертикальною стінкою і злегка заокругленою по верхніх краях прямокутною головкою. У розвинених країнах зварні рейки замінили рейки, що раніше застосовувалися, завдовжки 12 м, що скріплялися на стиках двоголовними накладками з болтами і гайками. Такі рейки забезпечують безпечніший рух складів без вертикального трясіння на стиках; саме стики найшвидше зношувалися, і їх скасування істотно понизило об'єми ремонтних робіт. Зазвичай між шпалою і підставою рейки вставляється сталева підкладка, чим забезпечуються те, що міцніше скріпляє рейки з шпалою і зменшення зносу внаслідок динамічних ударних навантажень від рухомого складу.
Шпали і баласт. У Західній Європі, Японії і інших місцях, де лісоматеріалів мало і вони дорогі, шпали зазвичай роблять із залізобетону. У США до цих пір широко застосовуються дерев'яні шпали із спеціальним просоченням.
Баласт виконує двояку роль: він служить подушкою шляху і дренирующим шаром для відведення дощової води з полотна. Зазвичай якнайкращим баластом вважається щебінь з твердих скельних порід, роздроблених на шматки розмірами близько 5 см, але як баласт можна використовувати також відходи гірничодобувної промисловості, гальку, гравій і інші подібні матеріали.
У результаті верхній будові додається деяка пружність, завдяки чому рейковий шлях при русі по ньому потягів злегка зміщується вгору-вниз, подібно до пружини. Проте на станціях, в тунелях і на мостах рейковий шлях укладається на жорстку підставу із сталі або бетону.
Ширина рейкової колії. Ширина колії не одна і та ж всюди. Стандартна колія шириною 1,435 м прийнята майже скрізь в Північній Америці і на основних залізничних магістралях країн Західної Європи. Вона ж характерна для Китаю і багатьох інших районів миру. Різновиди широкої колії (з відстанню між рейками шляху від 1,52 до 1,68 м) типові для республік колишнього СРСР, Аргентини, Чилі, Фінляндії, Індії, Ірландії, Іспанії і Португалії. Шляхи з вужчою колією (від 0,6 до 1,07 м) звичайні для Азії, Африки, Південної Америки, а також для другорядних залізниць Європи, особливо в гористій місцевості, і доріг лісовозів Росії.
Кривизна шляху і ухили. Не можна прокласти залізницю взагалі без поворотів, спусків і підйомів, але всі вони знижують ефективність перевезень, бо приводять до обмежень швидкості, довжини і ваги потягів і до необхідності допоміжної тяги. У зв'язку з цим при будівництві залізниць зазвичай використовуються всі можливості для того, щоб зробити дорогу прямо і рівніше.
Нахили на більшості залізничних магістралей не перевищують 1% (т.б. перепад рівня полотна дороги 1 м на її довжині 100 м) від довжини по горизонталі. Нахили, що перевершують 2%, на головних залізницях зустрічаються рідко, хоча в горах бувають і більше 3%. Підйом в 4% для звичайного локомотива практично неможливий, але з ним легко справляється локомотив, оснащений колесом з механізмом зубчатого зачеплення з кремальерою шляху.
Дефекти осей колісних пар
Дефекти, що виникають в осях колісних пар протягом терміну їх служби, можуть бути класифіковані по двох групах.
Дефекти першої групи- виробничі; їх запобігання досягається шляхом вдосконалення технологічних процесів і контрольних операцій на підприємстві-виробнику. Дефекти другої групи- експлуатаційні пошкодження, в основному втомного характеру; запобігти їм, в принципі, не можна, але можна своєчасно виявляти в процесі огляду із застосуванням методів неруйнівного контролю до того, як вони досягнуть небезпечної стадії розвитку.
Поєднання профілактичних заходів, здійснюваних в процесі виготовлення і експлуатації (технічного обслуговування), до теперішнього часу в основному забезпечувало безпеку руху. Проте бажання понизити експлуатаційні витрати хоч би за рахунок збільшення міжремонтних пробігів ставить проблеми глибшого вивчення причин виникнення що підлягають усуненню дефектів. Перша проблема стосується корозійних пошкоджень, ефективним способом запобігання яким є нанесення захисного лакофарбного покриття, друга поверхневих пошкоджень, найчастіше виникаючих унаслідок ударів частинок баласту, вірогідність яких зростає у міру зростання швидкості руху потягів.
Визначено два напрями вирішення другої проблеми. Як одне з них розглядають механічний захист (прикриття) осей від вказаних дій. Практичні способи захисту існують, але вони, з одного боку, утрудняють огляд і технічне обслуговування осей, з іншого боку, немає гарантії в тому, що вони надійні у випадках особливо сильних точкових ударів. Отже, викликає цікавість інший напрям- вивчення впливу ударів на цілісність осі для кращого розуміння закономірностей розвитку пошкоджень в цілях його прогнозування і контролю.
Дані дослідження були присвячені впливу надрізів, що виникають в результаті ударів частинок баласту, на зародження і розвиток тріщин в металі осі.
Характер ударних навантажень
В процесі численних спостережень під мікроскопом поверхні осей з надрізами від ударів частинок баласту встановлена різноманітність конфігурацій надрізів. Сліди від більшої частини ударів мають вид численних подряпин і вибоїн невеликої глибини, тоді як від інших, спостережувані рідше, - надрізів завглибшки до 2 мм складної форми з гострими кутами. Більш того, у випадках найбільш сильних ударів виявлявся феномен адіабатичного зрізу, явища того ж типу, що має місце при випробуваннях броньової сталі шляхом обстрілу з дуже високою швидкістю (de/dt = 104 ? 105 с-1). Це доводить, що вісь може піддаватися таким інтенсивним ударним навантаженням, в результаті яких відбуваються квазіадіабатичні деформації.
В ході спостережень визначено багато параметрів мікронадрізів, що впливають на характер тріщіноутворення. До цих параметрів відносяться глибина і профіль мікронадрізу, від яких залежить розподіл напруги, ступінь холодної спайки і наявність смуг адіабатичного зрізу.
В зв'язку з цим цікаво відзначити, що виникнення мікронадрізу від удару з великою швидкістю супроводжується двома протилежно діючими ефектами. Холодний наклеп і залишкова напруга стиснення в зоні мікронадрізу уповільнюють розвиток тріщини, а концентрація напруги в осі, навпаки, прискорює його.
Сильні удари сприяють початку втомного тріщиноутворення, і тому, очевидно, необхідно знайти відповідь на наступне питання: якщо вісь піддається ударам і зона ударної дії не співпадає з місцеположенням тріщин, які можна виявити методами неруйнівного контролю (дефектоскопії), вживаними при огляді, чи можна гарантувати безпеку експлуатації до найближчого заходу на технічне обслуговування.
Це питання вимагає глибших знань в трьох наступних аспектах:
· визначення умов початку виникнення тріщин;
· оцінка впливу мікронадрізів на розвиток тріщин;
· оцінка темпів розвитку тріщин з урахуванням того, що реальний термін служби осей по пробігу приблизно рівний трьом циклам технічного обслуговування і ремонту.
Виникнення тріщин
Виникнення тріщин під впливом тривалих навантажень розглядали як результат концентрації напруги унаслідок экструзії/інтрузії смуг постійного ковзання (Рис. 1).
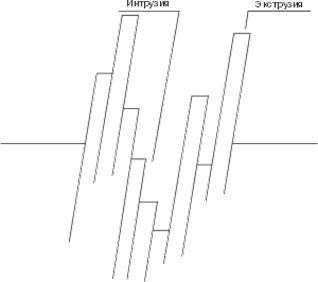
Рис. 1. Схема утворення інтрузій/экструзій на поверхні металу
Дослідження дозволили визначити декілька стадій процесу:
· утворення смуг постійного ковзання в зернах фериту;
· поява экструзії/інтрузії;
· виникнення уздовж інтрузій мікротріщин і не зв'язаних між собою тріщин невеликої довжини;
· розвиток тріщин переважний в зернах фериту уздовж інтрузій в кожному зерні або уздовж меж між зернами фериту і перліту.
Розвиток в основному відбувається під кутом 45° щодо напряму максимальної напруги вигину.
Потім, починаючи з певної довжини, відбувається злиття коротких тріщин в довгі, які розвиваються перпендикулярно напряму максимальної напруги і упоперек зерен перліту.
Одним із завдань досліджень було визначення межі між стадіями зародження і розвитку тріщин в сталях, вживаних для виготовлення осей.
Експерименти проводили на відшліфованих випробувальних зразках , на яких зручно відстежувати виникнення первинних коротких тріщин і відповідно початку стадії розвитку їх перетворення на довгі з одночасним визначенням глибини тріщин по їх формі.
Спостереження за тріщинами з вимірюванням їх довжини в ході досліджень здійснювали за допомогою електронного мікроскопа по методу реплікації. Довжину можна співвіднести з глибиною, визначуваною після шліфовки в різних місцях по фронту тріщини. Крім того, виконуючи мікроскопічні зрізи, можна візуально прослідкувати еволюцію орієнтації тріщин.
Результати досліджень дозволили встановити граничну глибину тріщини 300 мкм, після якої починається стадія розвитку.
Слід зазначити, що до вказаного значення глибини тріщини практично не піддаються виявленню засобами дефектоскопії. Отже, можна припустити, що осі, на яких в процесі поточного огляду дефекти не виявлені, все ж таки можуть мати тріщини, що знаходяться на стадії виникнення або на переході до стадії розвитку.
Вимоги до земляного полотна
Необхідність підвищення пропускної спроможності залізничних ліній, а також збільшення частки залізничного транспорту в перевезеннях пред'являє підвищені вимоги до інфраструктури і, зокрема, до земляного полотна.
Регламентуючі документи
Проектування, будівництво і технічний зміст земляного полотна в Німеччині здійснюють відповідно до норм DS 836. Геотехнічні вимоги в цій інструкції відносяться виключно до шляху на баласті, причому вони дані для двох діапазонів швидкості: до 160 км/г і більше 160 км/г. Ці вимоги повинні виконуватися як при реконструкції тих, що існують, так і при будівництві нових ліній на баластній підставі для швидкісного руху.
Геотехнічні вимоги до земляного полотна безбаластного шляху містяться у відповідному каталозі, який є доповненням до DS 836. На Державних залізницях Німеччини (DBAG) крім цього введені додаткові технічні умови і рекомендації по виконанню земляних робіт.
Геотехнічні вимоги
До несучих шарів земляного полотна пред'являють певні вимоги відносно розмірів, виду грунту, його щільності і водопроникності. При цьому завжди слід віддавати перевагу земляному полотну і грунту, що володіє рівномірно розподіленою несучою здатністю і щільністю, тим більше що існує метод проведення земляних робіт з суцільним динамічним контролем ущільнення (FDVK), що дозволяє виявити дефектні місця.
Жорстка підстава безбаластного шляху створює інші (в порівнянні з баластним) умови навантаження розташованих під ним шарів грунту. У зв'язку з цим до них пред'являються інші вимоги, зокрема, потрібна мінімальна деформованість. На нових лініях, що реконструюються, є відмінності як в товщині захисних шарів, так і у вимогах до несучої здатності і щільності.
Порівняння геотехнічних вимог до баластних і безбаластних шляхів стосовно нових ліній, що реконструюються, показало, що до шляху на жорсткій підставі вимоги значно вищі.
2.2 Дослідження напруженого стану плями контакту колеса і рейки
Взаємодія колеса і рейки є фізичною основою руху рухомого складу по залізницях. Від параметрів цієї взаємодії багато в чому залежать безпека руху і основні техніко-економічні показники господарств шляху і рухомого складу. Так, зокрема, втрати енергії, обумовлені зношуванням в системі колесо-рейка, складають 10% - 30% паливно-енергетичних ресурсів, що витрачаються на тягу. Крім того, витрати на реновацію рейок і колісних пар складають чималу частину загальних витрат дистанцій шляху і локомотивних і вагонних депо відповідно. Особливо великі витрати у зв'язку з цими витратами несуть локомотивні депо, оскільки за останні півстоліття середній термін служби локомотивної колісної пари істотно скоротився.
Серед причин, що викликали в 60-х – 80-х роках минулого сторіччя значне зростання інтенсивності зношування колісних пар, слід зазначити заміну самшитових підшипників ковзання підшипниками кочення, збільшення довжини і маси потягів, звуження колії до 1520 мм, введення профілю рейок (1979г.), що передбачає двоточковий контакт бандажа з головкою рейки та інші. Все це в сукупності призвело до істотної зміни навантаження зони контакту, температури і умов змазування в цій зоні, а також до зміни середньостатистичній швидкості ковзання колеса в поперечному щодо головки рейки напрямі. Результатом цих змін стало істотне зростання інтенсивності зношування коліс рухомого складу, яке, у свою чергу привело до катастрофічних результатів для локомотивного господарства: до кінця дев'яностих років витрати на реновацію колісних пар досягли неприпустимо великих розмірів.
На мал. 1. і 2. представлені графіки заповнення мережі залізниць Росії загартованими рейками [1] і діаграми структури обточувань колісних пар по експлуатаційному парку локомотивів на мережі залізниць Російської Федерації за 1999 і 2002 рр. [2].
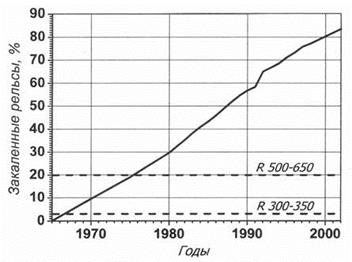
Рис.2 - Заповнення мережі залізниць Росії загартованими рейками
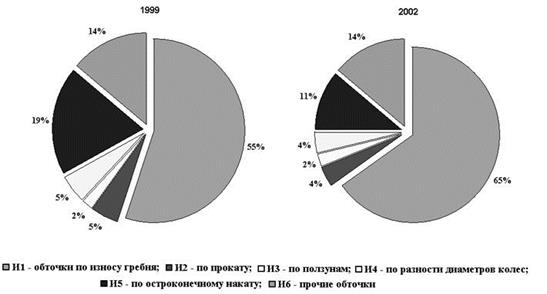
Рис.3 - Структури обточувань колісних пар по експлуатаційному парку
локомотивів на мережі залізниць Російської Федерації за 1999 і 2002 рр.
З порівняльного аналізу діаграм очевидно, що одночасно із зростанням питомої ваги об'ємно загартованих рейок зростає і частка обточувань по зносу гребеня. Така інтенсивність зносу викликала зростання експлуатаційних витрат в локомотивному і вагонному господарствах, пов'язаних з позаплановими обточуваннями колісних пар, додатковим придбанням нових бандажів і коліс.
Відзначимо, що обточування коліс, досягши товщини гребеня мінімального значення, пов'язане із зрізом більшого об'єму металу (так званий технологічний знос) з поверхні катання. Це істотно скорочує термін служби бандажа Рис.4.
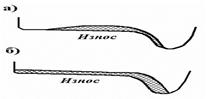
Рис.4- Профіль зносу гребеня:
а – профіль зносу 1960 р., б – профіль зносу 1986 р.
З метою зниження інтенсивності зношування КП до прийнятних значень останніми роками проводиться ряд заходів технічного і організаційно-технологічного характеру [3] (поліпшення конструкції шляху і рухомого складу, вдосконалення геометрії профілю поверхні катання КП і рейок, підвищення якості їх металу і т.д.). На жаль жодне з цих заходів в повному об'ємі проблеми не вирішило.
Кардинальне рішення питання може бути знайдене тільки на базі використання наукових знань в області взаємодії пари колесо-рейка. Необхідне проведення науково обгрунтованої модернізації колісних пар з одночасною розробкою заходів, що забезпечують ефективну експлуатацію і ремонт модернізованих колісних пар.
До технологічних заходів щодо зниження зносу бандажів колісних пар локомотивів відносяться наступні заходи: дослідження процесу взаємодії колеса з рейкою і дія на чинники, що впливають на швидкість зношення бандажа, конструктивні заходи щодо підвищення ресурсу, технологічні методи зміцнення бандажів, зменшення тертя між бандажем і рейкою, контроль і прогнозування технічного стану і ін. (Рис.5.).
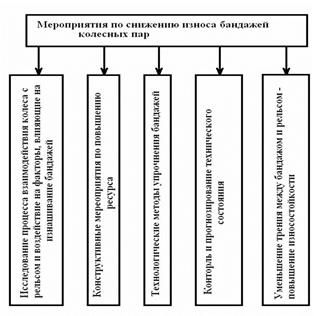
Рис.5- Заходи щодо зниження зношення бандажів колісних пар
На зносостійкість пари “колесо – рейка” за даними [4] впливають: твердість матеріалу бандажів, рейки, вміст вуглецю, структура металів і вміст сірки. Твердість металу є одним з найбільш важливих чинників, які впливають на зношення коліс рухомого складу. Впровадження за останнє десятиліття термічної обробки рейок і додання їм твердості 360 НВ безперечно зіграло важливу роль в поліпшенні роботи залізниць. Проте із зміною твердості рейок заходів по підвищенню твердості бандажів зроблено не було. В результаті відношення твердостей сталі колеса і рейки стало 0,75, це істотно змінило характер зносу в парі “колесо – рейка”. У дослідженнях Вніїжта [4], [5] 1960 – 1990х років наголошувалося, що для рівної зносостійкості відношення твердості колісного зразка до твердості рейкового зразка повинне бути близько 1,2 при прослизанні до 1%, а при прослизанні до 10% – 1,0 – 1,1.
Таким чином, встановлення оптимальної твердості поверхні катання колеса є складним завданням, рішення якого повинне здійснюватися системно з обліком, різних параметрів, а величина твердості поверхні катання коліс на сьогоднішній час обмежена величиною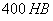 
.
Розробка ефективних методів зниження ступеня зносу залежить від наявності методик дослідження, оцінки параметрів контактної взаємодії пари “колесо – рейка” за допомогою чисельних методів.
Завдання контакту кочення двох пружних тіл, що мають однакові характеристики пружності, як для колеса і рейки, може бути представлене роздільно у вигляді нормального і тангенціального завдань. Мета першого завдання полягає у визначенні розміру і форми площадки контакту, а також розподіли нормальної контактної напруги. Результати вирішення нормальної задачі використовуються для знаходження рішення тангенціальною, такою, що полягає в знаходженні розподілу дотичної напруги і моменту в зонах зчеплення і прослизання контактної площадки.
Г. Герц дав перше надійне математичне рішення нормальної задачі. Відстань між недеформованими тілами може бути знайдена геометрично, якщо відомі радіуси кривизни тіл в точці контакту. Пружні властивості колеса і рейки, що описуються коефіцієнтом Пуассона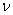 
і модулем пружності, вважаються однаковими. Якщо тіла навантажені нормальною силою, з'являється зона контакту еліптичної форми з великою напіввіссю у напрямі подовжньої осі рейки представленою на Рис.6.
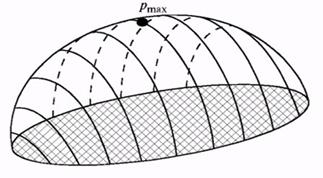
Рис.6 - Розподіл нормальної герцевської напруги на площадці контакту
Максимальна контактна напруга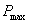 
може бути розрахована по формулі:
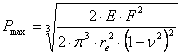(1)
де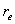 
еквівалентний радіус, залежний від характерних радіусів взаємодіючих тіл (колеса і рейка) в місці контакту.
Таким чином, нормальна напруга на поверхнях катання рейки і колеса залежить від навантаження від колеса на рейку, радіусів поверхонь катання колеса і рейки, властивостей взаємодіючих матеріалів.
Слід мати на увазі, що контактна теорія Герца справедлива при наступних допущеннях:
контактуючі поверхні однорідні і ізотропні;
сили тертя в зоні контакту не діють;
розмір контактної площадки малий в порівнянні з розмірами контактуючих тіл і характерними радіусами кривизни недеформованих поверхонь;
для контактного завдання використано вирішення лінійного пружного напівпростору;
контактуючі поверхні гладкі.
При русі екіпажу положення колісної пари по відношенню до рейок істотно міняється, приводячи до виникнення різних поєднань контактних зон колеса і рейки.
Навіть за умови постійного осьового навантаження нормальна напруга істотно мінятиметься внаслідок відмінності в радіусах кривизни контактуючих поверхонь цих зон.
Якщо в області контакту має місце один радіус кривизни поверхні, можна використовувати рішення Герца. Якщо в області контакту є два або декілька радіусів кривизни, наприклад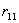 
і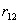 
(Рис.7.), рішення Герца несправедливе, і для визначення майданчика контакту слід використовувати негерцівське рішення. Це особливо важливо при різноманітних поєднаннях зношених профілів колеса і рейки.
При знаходженні нормальної контактної напруги для неконформного негерцівського контакту використовуються різні методи і програми. Зокрема, повне розв’язання негерцевскої задачі може бути знайдене за допомогою програми CONTACT [6]. Проте через те, що вирішення задачі за допомогою цієї програми вимагає великого часу, запропоновані різні варіанти наближеного розв’язання негерцівської задачі. Наприклад, з використанням методу апроксимації негерцівській геометрії еліпсами отримані результати, в достатній мірі що узгоджуються з точним рішенням (Рис.7.) [7].
Інший підхід, що використовується для знаходження контактної напруги між зношеним колесом і рейкою, полягає в моделюванні контактуючих тіл з використанням пружної підстави, при якій деформація поверхонь пропорційна нормальній контактній напрузі [8]. Отримана при цьому максимальна контактна напруга буде в 1,3 більше, ніж при герцівському розв’язанні. Розмір площадки контакту і розподіл нормальної напруги залежать від нормального навантаження, що діє від колеса на рейку, профілів колеса і рейки, поперечного і кутового положення колісної пари на рейках і подуклонки рейок.
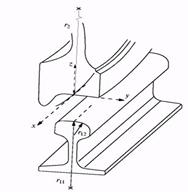
Рис.7 - Геометрія контакту колеса і рейки:
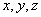осі системи координат; 
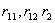характерні радіуси ( 
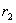– радіус профілю колеса)
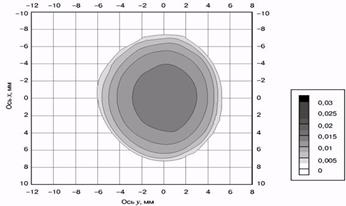
Рис.8 - Форма площадки контакту і розподіл тиску:
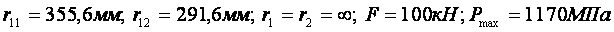
Колісна пара може контактувати з рейкою в двох різних точках [9]. Двоточковий контакт приводить до утворення двох площадок контакту: А на поверхні катання рейки і В на бічній поверхні головки рейки в районі викружки (Рис.9.,а). Внаслідок того що колісна пара при русі в кривій переміщається з деяким кутом набігання а, площадка контакту В зрушена вперед (мал. 8.,б). Збільшення кута набігання приводить до збільшення відстаней між площадками контакту (забігу) і до миттєвої осі обертання колісної пари і тим самим до зростання відносного прослизання і тангенціальної сили, що з ним зв'язана. У зоні того, що стосується гребеня колеса і робочої грані головки зовнішньої рейки рівень розрахункової контактної напруги може досягати 3000 Мпа.
При контакті сильно зношеної рейки з новим або зношеним колесом змінюється форма області розподілу тиску. Розмір площадки контакту істотно зменшується, він зрушується до зовнішньої поверхні зовнішньої рейки, приводячи до збільшення контактного тиску, рівень якого може досягати межі текучості, що викликає пластичну деформацію головки рейки.
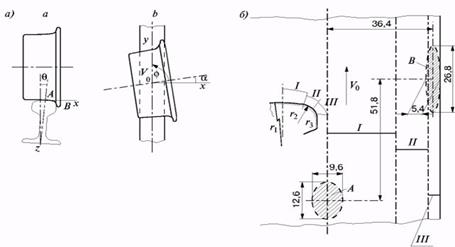
Рис.9 - Положення і розміри контактних майданчиків при двоточковому контакті колеса і рейки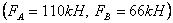 
:
а) А, В – точки контакту колеса з рейкою; 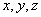осі координат 
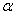кут набігання колеса на рейку; 
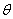кут подуклонки рейки; 
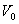вектор швидкості руху колісної пари б) А, В – майданчики контакту; I, II, III – області контакту; 
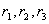радіуси кривизни головки рейки
Зазвичай контактна напруга на поверхні катання (область А) колеса вантажного вагону знаходиться в межах 1300 – 1700 Мпа. Збільшення осьового навантаження приводить до зростання контактної напруги пропорційно до її величини (див. формулу 1).
Якщо поверхня катання колеса має прокат з поперечним профілем, що утворився, це призводить до істотного збільшення контактного тиску, який може мати місце по обох сторонах цього профілю. Так, при величині прокату профілю 2 мм розрахункова контактна напруга на обох краях може досягати 6000 Мпа, що свідчить про значний пластичний перебіг матеріалів.
Висока контактна напруга виникає у випадках, якщо профіль колеса своїм зовнішнім краєм спиратиметься на рейку або контактна зона не досягає зовнішнього краю колеса, приводячи до виникнення виступу (фальшивого гребеня) в області зовнішньої частини поверхні катання колеса.
Величина і розподіл контактної напруги істотно залежать від профілів колеса і рейки і від того, який має місце контакт: одноточковий або двоточковий. При конформному профілі розмір площадки контакту збільшується, приводячи до зменшення рівня контактної напруги в порівнянні з неконформними профілями.
Таким чином для оцінки загального напруженого стану в парі колесо-рейка досить вирішити завдання Герца для одноточкового контакту бандажа і рейки. Вирішення задачі проводилося в програмному комплексі ANSYS.
При побудові моделі “колесо – рейка” і проведенні розрахунків розглядався тип рейки Р65 по ГОСТ 18267 – 82, і бандаж ГОСТ 398 – 96, при цьому розглядався незношений профіль бандажа і рейки. Механічні властивості бандажа і рейки, що використовуються для розрахунку представлені в таблиці 1.
Таблиця 1
Механічні властивості бандажа і рейки
| Механічні властивості | Бандаж ГОСТ 398 – 96 | Рейка ГОСТ 18267 – 82 |
| Щільність, кг/м3 | 7850 | 7850 |
| Модуль Юнга, Па |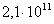 
|
|
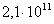
| Коефіцієнт Пуассона | 0,3 | 0,3 |
Схема сил, що завантажують колісну пару, представлена на малюнку 9.
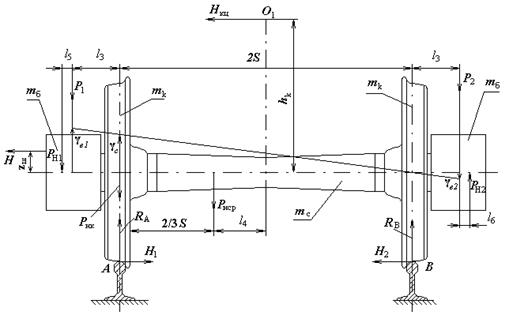
Рис.10. Схема сил, що завантажують колісну пару
У глобальній декартовій системі координат проводилося розбиття колісної пари на тетраедричні кінцеві елементи. Кінцево елементна сітка представлена на Рис11.
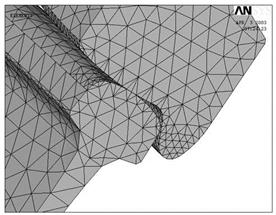
Рис.11. Кінцево елементна модель пари “Колесо - рейка”
На Рис.12 представлена эпюра розподілу напруги в парі “колесо - рейка”.
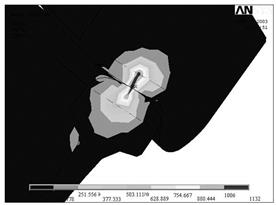
Рис.12. Эпюра розподілу напруги в контакті пари “Колесо - рейка”
При розрахунку було виявлено, що в зоні контакту на поверхні катання колеса напруги досягають значних величин, але вони локалізовані в межах невеликої області. Розмір цієї області порівняємо з розміром плями контакту.
Висновки
1. Встановлення оптимальної твердості поверхні катання колеса є складним завданням, вирішення якого повинне здійснюватися системно, з обліком, різних параметрів.
2. Твердість поверхні катання коліс в даний час обмежена величиною .
3. Напруга локалізована в межах малої області колеса і рейки. Розмір області порівняємо з розміром плями контакту.
4. Повздовжні зусилля, що виникають при різних режимах гальмування, є одним з основних показників, що враховуються в тягових розрахунках і розрахунках на міцність потягів.
5. Розроблена і підтверджена практикою експлуатації методика для оцінки повздовжніх динамічних зусиль і гальмівних шляхів у вантажних потягах і показаний вплив характеристик гальм на динаміку потягу.
6. Математична модель руху поїзда є необхідною і невід’ємною часткою розвитку сучасної транспортної системи.
Література
1. Лисицын А.Л., Мугинштейн Л.А., Терещенко В.П. Поезда повышенного веса и длины. Опыт, проблемы, возможности // Железнодорожный
2. П. Динамика торможения тяжеловесных поездов. М.: Транспорт, 1977. 151 с.
3. Ступин Д.А., Беляев В.И. Разработка российского эластомерного поглощающего аппарата для автосцепного устройства грузовых вагонов // Вестник ВНИИЖТ. 1998. № 6. С. 29...31.
4. Исследование динамики поезда с гидрогазовыми поглощающими аппаратами ГА-500 / С.В. Вершинский, П.Т. Гребенюк, Г.В. Костин, А.Д. Кочнов, Ю.М. Черкашин / Сб. науч. тр. ВНИИЖТ. Вып. 649. М.: Транспорт, 1982. С. 49...65.
5. Баранов Л.А. Потенциальная оценка пропускной способности железнодорожной линии по системам обеспечения безопасности // JYЖЕЛ: «The 7th International scientific conference of railway experts». Yugoslavia, Vrnjacka Banja: 2000. Р. 43...49.
6. Расчет и оптимизация координатного сближения поездов метрополитена / Л.А. Баранов, А.А. Моисеев, В.М. Абрамов, В.Н. Полоцкий // Вестник ВНИИЖТ. 1992. № 6. С. 24...28.
7. Шур Е.А. К вопросу об оптимальном соотношении твердости рельсов и колес //Современные проблемы взаимодействия подвижного состава и пути: Материалы научно-практической конференции/ ВНИИЖТ. – М., 2003. с. 87 – 93.
8. Бартенева Л.И. Технология лубрикации боковой поверхности рельсов передвижными рельсосмазывателями – комплексное решение проблемы износа в контакте гребень колеса – рельс //Современные проблемы взаимодействия подвижного состава и пути: Материалы научно-практической конференции/ ВНИИЖТ. – М., 2003. с. 114 – 122.
Вступ
Математична модель в механіці - це замкнута система математичних співвідношень, що дозволяє з прийнятною точністю вивчати особливості поведінки даного об'єкту, що цікавлять дослідника.
Математичне моделювання в механіці керованих систем має ряд особливостей:
· Що вивчаються в механіці керованого руху об'єкти надзвичайно різноманітні. Автомобіль, гіроскопічний стабілізатор, крокуючий робот, імітатор космічного польоту і т.п. складаються з різних жорстких конструктивних елементів, пристроїв, датчиків, двигунів. З теоретико-механічної точки зору всі ці об'єкти можуть розглядатися як системи, що складаються з великого числа взаємодіючих твердих тіл. Спроба скласти математичну модель такого об'єкту за допомогою класичних методів теоретичної механіки, наприклад у формі рівнянь Лагранжа, зазвичай приводить до неймовірно громіздких рівнянь, що налічують сотні і тисячі доданків. Виникає потреба в наближеному моделюванні, яке для чітко обумовленого класу руху описує потрібні явища з прийнятною точністю.
· Для систем, керованих рухів, що вивчаються механікою, характерні сильні загасання високочастотних власних складових руху. Наближене моделювання таких систем тяжіє до побудови розкладань А. Пуанкаре і погрансольним методам А.Н. Тихонова - А.Б. Васильєвої.
Проникнення математичних методів в найрізноманітніші, часом несподівані сфери людської діяльності означає можливість користуватися новими, як правило, вельми плідними засобами дослідження. Зростання математичної культури фахівців у відповідних областях призводить до того, що вивчення загальних теоретичних положень і методів обчислень вже не становить серйозних труднощів. Але на практиці виявляється, що одних лише математичних пізнань далеко не достатньо для вирішення того або іншого прикладного завдання необхідно ще отримати навики в перекладі початкового формулювання завдання математичною мовою.
Ситуації моделюють для різних цілей. Головна з них необхідність передбачати нові результати або нові властивості явища. Ці прогнози можуть бути пов'язані з розповсюдженням існуючих результатів або мати принциповіший характер. Часто вони відносяться до умов, які, ймовірно, матимуть місце в деякий момент в майбутньому. З іншого боку, прогнози можуть відноситься до подій, безпосереднє експериментальне дослідження яких нездійсненно. Найбільш важливий приклад такого роду дають численні прогнози, які робилися на основі математичних моделей в програмі космічних досліджень. Проте для цієї мети моделюються не всі ситуації: в деяких випадках досить вміти описувати математичними засобами роботу системи для того, щоб добитися глибшого розуміння явища (саме цю роль і грають багато видатних фізичних теорій, хоча на їх основі робляться також і прогнози). Зазвичай при такому математичному описі не враховується елемент контролю, проте в моделях, побудованих, наприклад, для дослідження роботи мереж, таких як схеми руху потягів або літаків, контроль часто є важливим чинником.
Математична модель є спрощенням реальної ситуації. Відчутне спрощення наступає тоді, коли неістотні особливості ситуації відкидаються і складне початкове завдання зводиться до завдання, що ідеалізується, піддається математичному аналізу. Саме при такому підході в класичній прикладній механіці виникли блоки без тертя, невагомі нерозтяжні нитки, нев'язкі рідини, абсолютно тверді або чорні тіла і інші подібні моделі, що ідеалізуються. Ці поняття не існують в реальній дійсності, вони є абстракціями, складовою частиною ідеалізації, зробленій автором моделі. І проте їх часто можна з успіхом вважати хорошим наближенням до реальних ситуацій. Описаний образ дій при побудові математичних моделей не є єдиним, і цьому зовсім не варто дивуватися. У іншому можливому підході першим кроком є побудова простій моделі декількох найбільш характерних особливостей явища. Це часто робиться для того, щоб відчути дане завдання, причому робиться це ще до того, як саме завдання остаточно сформульоване. Потім ця модель узагальнюється, щоб охопити інші факти, поки не буде знайдено прийнятне або адекватне рішення. Є ще підхід, коли із самого початку вводиться в розгляд одночасне велике число чинників. Він часто застосовується в дослідженні операцій, і такі моделі зазвичай вивчають імітаційними методами з використанням ЕОМ.
Актуальність теми. Одна з основних проблем сучасного локомотивобудування - забезпечення високих тягових і динамічних характеристик локомотивів, які в основному визначаються конструкцією екіпажної частини і технічним станом системи колесо - рейка.
У останні десятиліття з метою зменшення силової взаємодії і зносу гребенів коліс і рейок в кривих велася цілеспрямована і системна робота по впровадженню нових профілів коліс і технологій змазування гребенів і рейок. Це значно понизило гостроту проблеми виходу з експлуатації рейок і бандажів локомотивних коліс внаслідок підвищеного зносу. В той же час збільшилася контактно-втомна пошкоджуваність коліс і рейок.
Дослідження динаміки локомотивів і зношування гребенів в більшості теоретичних і експериментальних робіт виконувалися на вибігу, а не під тягою, при контакті нових коліс, у тому числі і з криволінійним профілем, з новими або мало зношеними рейками і без змазування.
Вивчення динаміки з погляду силової взаємодії і зношування гребенів коліс локомотива в режимах вибігу і тяга при різному технічному стані системи колесо - рейка є актуальним завданням.
Розділ 1. Опис фізичних явищ, що впливають на рух поїзда
Дата: 2019-05-28, просмотров: 197.
