Приток жидкости к несовершенной скважине даже в горизонтальном однородном пласте постоянной толщины перестаёт быть плоскорадиальным. Строгое математическое решение задачи о притоке жидкости к несовершенной скважине в пластах конечной толщины представляет большие (а в некоторых случаях непреодолимые) трудности.
Приведём здесь без выводов и доказательств наиболее распространённые окончательные расчётные формулы притока жидкости к различного типа несовершенным скважинам.
Прежде всего допустим, что скважина вскрыла кровлю пласта неограниченной толщины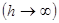 
и при этом её забой имеет форму полусферы.
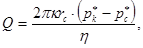(3.25)
где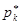 
и 
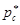- приведённые давления.
Если скважина вскрыла пласт неограниченной толщины на глубину b, то её дебит можно найти по формуле Н.К. Гиринского:
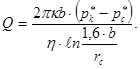(3.26)
Задача о притоке жидкости к несовершенной по степени вскрытия пласта скважине в пласте конечной толщины h исследовалась М. Маскетом. Вдоль оси скважины на вскрытой части длиной b он располагал воображаемую линию, поглощающую жидкость, каждый элемент которой dz является стоком. Интенсивность расходов q, т.е. дебитов, приходящихся на единицу длины поглощающей линии, подбиралась различной в разных её точках для выполнения нужных граничных условий.
Необходимо получить решение, удовлетворяющее следующим граничным условиям: кровля и подошва пласта непроницаемы; цилиндрическая поверхность радиусом r =R является эквипотенциалью Ф =Ф; поверхность забоя скважины также является эквипотенциалью Ф =Ф.
Выполнение указанных граничных условий потребовало отображения элементарных стоков qdz относительно кровли и подошвы пласта бесчисленное множество раз.
Подбирая интенсивность расходов q и используя метод суперпозиции действительных и отображённых стоков, М. Маскет получил следующую формулу для дебита гидродинамически несовершённой по степени вскрытия пласта скважины:
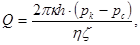(3.27)
где
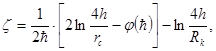(3.28)
а функция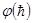 
имеет следующее аналитическое выражение:
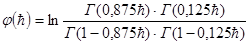(3.29)
Здесь
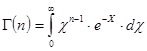
- интеграл Эйлера второго рода, называемый гамма - функцией, для которой имеются таблицы в математических справочниках.
Нетрудно заметить, что если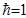 
, то есть пласт вскрыт на всю толщину, формула (3.28) переходит в формулу Дюпюи для плоскорадиального потока.
Иногда для расчёта дебита несовершенной по степени вскрытия пласта скважины используется более простая формула, чем (3.28) М. Маскета, предложенная И. Козени:
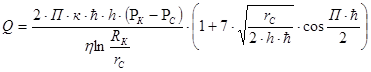(3.30)
Дебит несовершенной скважины удобно изучать, сравнивая её дебит Q с дебитом совершенной скважины Qсов, находящейся в тех же условиях, что и данная несовершенная скважина. Гидродинамическое несовершенство скважины характеризуется коэффициентом совершенства скважины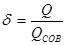 
.
Широкое распространение получил метод расчёта дебитов несовершенных скважин, основанный на электрогидродинамической аналогии фильтрационных процессов.
Электрическое моделирование осуществляется следующим образом. Ванна заполняется электролитом. В электролит погружается один кольцевой электрод, моделирующий контур питания. В центре ванны погружается электрод на заданную глубину, соответствующую степени вскрытия пласта скважиной. К обоим электродам подводится разность потенциалов, являющаяся аналогом перепада давления, сила тока служит аналогом дебита скважины. Дебит гидродинамически несовершенной скважины подсчитываются по формуле
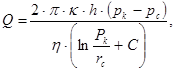(3.31)
где С=С1 +С2 - дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия пласта (С1) и характеру вскрытия (С2).
Измеряя разность потенциалов и силу тока, можно подсчитать сопротивление по закону Ома, сделать пересчёт на фильтрационное сопротивление и определить дополнительное фильтрационное сопротивление.
Такие экспериментальные исследования были проведены В.И. Щуровым. Им определены дополнительные фильтрационные сопротивления С и С для различных видов несовершенства скважин и построены графики зависимости С от параметров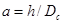 
и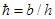 
(Рис.6.2) (см. Приложение), а также С от трёх параметров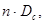 
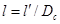и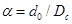 
(Рис.6.3) (см. Приложение), где n - число перфорационных отверстий на 1 м вскрытия толщины пласта; 
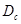- диаметр скважины; 
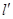- глубина проникновения пуль в породу; 
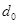- диаметр отверстий.
Выражение дополнительного фильтрационного сопротивления получено И.А. Чарным с использованием формулы Маскета (3.28) в виде
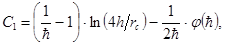(3.32)
где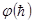 
определяется по формуле (3.30) или по графику
А.М. Пирвердян получил для коэффициента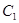 
следующее выражение:
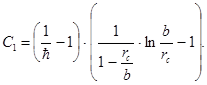(3.33)
Сравнив дебиты совершенной скважины (формула Дюпюи) и несовершенной скважины (3.31), получим выражение коэффициента совершенной скважины в следующем виде:
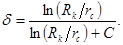(3.34)
Иногда бывает удобно ввести понятие о приведённом радиусе скважин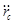 
, т.е. радиусе такой совершенной скважины, дебит которой равен дебиту данной несовершенной скважины:
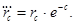(3.35)
Тогда (3.31) можно заменить следующей формулой:
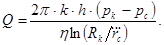(3.36)
И.А. Чарный предложил следующий способ определения дебита скважины, несовершенной по степени вскрытия, если величина вскрытия пласта b мала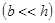 
. Область движения условно разбивается на две зоны (Рис.6.4). Первая - между контуром питания и радиусом 
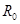, равным или большим толщины пласта 
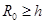, в этой зоне движение можно считать плоскорадиальным. Вторая - между стенкой скважины и цилиндрической поверхностью 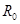, где движение будет существенно пространственным. Обозначим потенциал при r =R через Ф. Тогда для зоны 
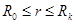можно записать формулу Дюпюи:
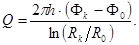(3.37)
Для зоны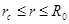 
, считая здесь приближённо движение радиально - сферическим между полусферами радиусами r и R, имеем:
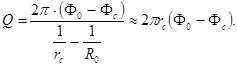(3.38)
Из формул (3.31) и (3.33) по правилу производных пропорций получается формула для дебита скважины:
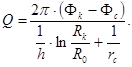(3.39)
Приняв R =1,5h, получим окончательно формулу для дебита несовершенной скважины, вскрывшей пласт на малую глубину:
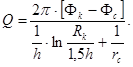(3.40)
Задачи притока жидкости к скважинам, гидродинамически несовершенным по характеру вскрытия пласта, и к скважинам с двойным видом несовершенства, ещё более сложны для исследования, чем приток к несовершенным по степени вскрытия пласта скважинам. Такого рода задачи решались теоретически М.М. Глоговским, А.Л. Хейном, М. Маскетом и другими исследователями. Все полученные ими решения весьма сложны. Наибольшее распространение в практике расчётов дебитов несовершенных скважин по характеру вскрытия пласта и с двойным несовершенством получили результаты теоретических и экспериментальных исследований, проведённых В.И. Щуровым, Г.Г. Поляковым, М.Н. Тиховым и М.С. Ватсоном.
Лабораторные исследования
Все образцы керна, пробы нефти, воды и газа, отобранные в процессе бурения и испытания скважин, должны подвергаться лабораторным исследованиям.
По образцам керна, взятым из интервалов залегания продуктивных пластов, определяются следующие параметры:
общая и открытая пористость,
проницаемость
остаточная водонасыщенность,
нефтенасыщенность,
карбонатность,
глинистость.
Образцы керна также подвергаются изучению на определение флоры, фауны и микрофауны, споропыльцевому анализу.
Производится также минералогический и гранулометрический анализы, как коллекторов, так и пород-покрышек.
Порядок отбора керна на лабораторные исследования таков - из одного, в смысле литологической изменчивости, слоя - через 0.25-0.30 м, из неоднородного слоя образцы отбираются через0.2 м и чаще.
По отборным пробам пластовых жидкостей и газа должны быть определены:
а) для нефти - фракционный и групповой составы, содержание селикагеливых смол, масел, асфальтенов, парафина, серы, а также вязкость и плотность (как в поверхностных - при температуре 20 градусов по Цельсию и давлении 0.1 Мпа, так и в пластов условиях), величина давления насыщения нефти газом, изменение объема и вязкости нефти при различных давлениях в пластовых и поверхностных условиях, коэффициенты упругости, при отборе глубинных проб-забойные давления и температуры, газовый фактор.
б) для пластовой воды - полный химический состав, включая определение ценных попутных компонентов (йода, брома, бора, лития и других элементов), количество и состав растворенного в воде газа, измерение температуры и электрического сопротивления вод.
в) для газа, растворенного в нефти, и свободного газа - плотность по воздуху, теплота сгорания, химический состав (объемные доли метана. Этана, пропана, бутанов, пентанов, гексанов и более тяжелых углеводородов в%, а также гели, сероводорода в граммах на 100 м3 газа, углекислоты и азота).
Таблица 3.3 - Перечень лабораторных исследований
| № | Наименование исследования, анализа | Интервал отбора | Кол-во образцов (проб) | Организация, выполняющая исследования |
| 1 | Определение общей пористости | 0.1-0.5 | 30-150 | СибНННП |
| 2 | Определение открытой пористости | 0.1-0.5 | 30-150 | СибНИИНП |
| 3 | Определение эффективной пористости | 0.1-0.5 | 30-150 | СибНИИНП |
| 4 | Определение проницаемости | 0.1-0.5 | 30-150 | СибНИИНП |
| 5 | Определение нефтенасыщенности | 0.1-0.5 | 30-150 | СибНИИНП |
| 6 | Определение коэффициента вытеснения | 0.1-0.5 | 30-150 | СибНИИНП |
| 7 | Определение остаточной водонасыщенности | 0.1-0.5 | 30-150 | СибНИИНП |
| 8 | Определение карбонатности | 1-2 | 7-15 | СибНИИНП |
| 9 | Определение глинистости | 1-2 | 7-15 | СибНИИНП |
| 10 | Минералогический анализ | 5-10 | 2-3 | СибНИИНП |
| 11 | Гранулометрический анализ | 5-10 | 2-3 | СибНИИНП |
| 12 | Микрофаунический анализ | 1-2 | 7-15 | СибНИИНП |
| 13 | Анализ шлама на содержание углеводородов | 1-5 | 1-3 | СибНИИНП |
| 14 | Анализы поверхностных проб нефти и газа | 3/на объект | 3 | ЮНИПИН |
| 15 | Анализы глубинных проб нефти и газа | 3/на объект | 3 | СибНИИНП ЮНИПИН |
| 16 | Анализы проб воды | 2/ на объект | 2 | СибНИИНП |
Дата: 2019-05-28, просмотров: 393.
