2.1. Тематическое планирование
Одним из существенных моментов в организации обучения является систематизация за знаниями и умениями учащихся. От того, как она организована, на что нацелена, существенно зависит содержание работы на уроке, как всего класса в целом, так и отдельных учащихся. Вся система систематизации знаний и умений учащихся должна планироваться таким образом, чтобы охватывались все обязательные результаты обучения для каждого ученика. Одновременно в ходе систематизации надо дать учащимся возможность проверить себя на более высоком уровне, проверить глубину усвоения материала. В ходе изучения темы учитель проверяет результаты обучения путем проведения текущих самостоятельных работ, устного опроса, систематизационных работ и других форм систематизации.
История развития математического знания даёт возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры.
Требования к знаниям и умениям учащихся в данном курсе не завышены. Так как чрезмерность требований порождает перегрузку, что ведёт к угасанию интереса к математике. Применение компьютерной технологии (презентации, слайды, поиск информации по имеющимся источникам) заинтересовывает учащихся данным курсом, что, помогая лучше овладеть ЗУН. Курс оснащён информационно-программным средством “Этот удивительный мир чисел, электронная версия”.
Цели курса: обобщение и систематизация, расширение и углубление знаний о множестве чисел, обретение практических навыков при выполнении тренировочных заданий, привитие устойчивого интереса к математике, повышение уровня математической подготовки школьников; увеличение количества учащихся, для которых математика станет профессионально значимым предметом.
Задачи курса:
· сформировать у учащихся логическое представление о числах; > восполнить пробелы в знаниях о числах;
· сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;
· сформировать навыки самостоятельной работы;
· сформировать умения и навыки исследовательской работы, работы со справочной литературой, с компьютером;
· способствовать развитию алгоритмического мышления, воспитанию умений действовать по данному алгоритму;
· показать, что источник возникновения изучаемых понятий - реальный мир, что они возникли из практических потребностей людей;
· показать, что понятия не изолированы друг от друга, а представляют определённую систему знаний, все звенья которой находятся во взаимной связи;
· способствовать развитию творческого и логического мышления учащихся;
· способствовать формированию познавательного и устойчивого интереса к математике;
· пополнить исторические сведения;
· обеспечить условия для расцвета личности школьника с учётом возрастных особенностей;
· привить навыки работы в группах, выступать, вести переговоры, отстаивать свое мнение и интересы;
· подготовка учащихся к профильной школе.
Календарно – тематическое планирование.
| №/№ | Тема занятий. | Кол - во часов. | Дата проведения. | Виды деятельности. | Оборудование. |
| 1. | Натуральные и целые числа. | Зч. | |||
| 1 | Натуральные числа. Система счисления. | 1ч. | Анкетирование, аукцион знаний, демонстр. презентации. | Лист ответов, компьютер, программ. обеспечение. | |
| 2 | 1ростые и составные числа. НОД (Алгоритм Евклида). | 1ч. | Исследов. работа, Работа со справочником, практикум. | Компьютер, программное обеспечение | |
| 3 | Множество целых чисел. Самостоятельная работа. | 1ч. | Беседа, работа со справочником. Самостоят. проверочная работа | Компьютер, программное обеспечение. Лист ответов. | |
| 2. | Рациональные числа. | 1ч. | |||
| 1 | Обыкновенные и десятичные дроби. Периодические дроби. - | 1ч. | Исследов. работа. Работа со справочником, практикум. | Компьютер, программное обеспе-ние . | |
| 3. | Действительные числа. | Зч. | |||
| 1 | Непериодические бесконечные десятичные дроби. Иррациональные числа. | 1ч. | 1екция, аукцион знаний. | Компьютер, программное обеспечение. | |
| 2 | Коредь 1с-й степени из действительного числа. | 1ч. | Работа со справочником, практикум. | Компьютер, программное обесп. | |
| 3 | Систематизацияное тестирование. | 1ч. | Самостоятельная работа. | Компьютер, лист ответов. | |
| 4. | Комплексные числа. | Зч. | |||
| 1. | Алгебраическая форма комплексного числа. Действия с комплексными числами. | 1ч. | Проблемная беседа Практикум. | Компьютер, программное обссп. | |
| 2. | Применение комплексного числа. | 1ч. | Лекция. | Компьютер, программное обесп. | |
| 3. | Систематизационное тестирование. | 1ч. | Самостоятельная работа. | Компьютер, лисе ответов. | |
| 5. | Круглый стол | 2ч. | Вопросы - ответы. Обсуждение. Анкетирование | Заготовленные вопросы. Лист ответов. | |
| Итого: | 12ч. |
Тест
Действительные числа
1. Обратить обыкновенную дробь в десятичную:
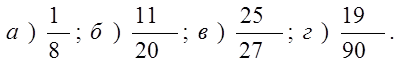
Ответ: а) 1) 0,102; 2) 0,125; 3) 0,1205.
б) 1) 0,55; 2)0,505; 3)0,255.
в) 1) 0,(925); 2) 0,9(25); 3) 0,92(5).
г) 1) 0;21; 2) 0,2(1); 3)0,(21).
2. Обратить десятичную дробь в обыкновенную:
а) 0,15; б) 0,225; в) 0,(6); г) 2,2(41).
Ответ: а) 1) 3/20; 2) 4/17; 3) 3/5.
б) 1) 9/40; 2) 2/19; 3) 1/40.
в) 1) 2/3; 2) 1/9; 3) 3/7.
г) 1) 2219/90; 2) 2219/990; 3)2219/999.
3)Выписать из данных чисел иррациональные:
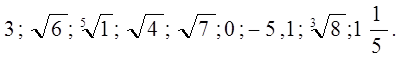
Ответ: а) 1)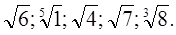 
2) 
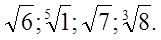
3) 
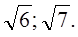
4. При каких х имеет смысл выражение:
А.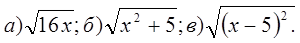 
Ответ: а) 1) х>0; 2) x <0; 3) x- любые числа.
б) 1) х>5; 2) x <5; 3) x- любые числа.
в) 1) х ≥5; 2) x ≤5; 3) x- любые числа.
Б.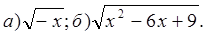 
Ответ: а) 1) х ≥0; 2) x ≤0; 3) x- любые числа.
б) 1) х ≥3; 2) x ≤3; 3) x- любые числа.
5* Упростить выражение:
Б.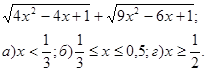 
Ответ: а) 1) 2-5х; 2) 5х-2; 3) x;
б) 1) 5х-2; 2) 2-5х; 3) x;
в) 1) 2-5х; 2) x; 3) 5х-2;
В.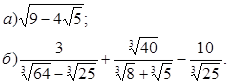 
Ответ: а)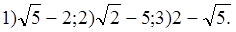 
б)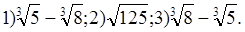 
Тест
Комплексные числа.
1. Изобразить комплексные числа на координатной оси: z1=4-6i ; z2=3+i ; z3=-5i ; z4=4-0i ; z5=-1,5=3i ; z1=-2-8i ;
2. Для комплексных чисел z1 и z2 найти:
1)z1+ z2; 2)z2- z1; 3) z1z2; 4) z1: z2:
z1 = 5-3i , z2 = -4+7i.
Ответ:1. а)z1+ z2=1+4i; б)z1+ z2 =4+i; в)z1+ z2=2+3i;
2. а)z2- z1=9-10i; б) z2- z1=-9+10i ; в)z2- z1= -9-10i ;
3. а)z1z2=-41+47i ; б) z1z2=-1-47i ; в)z1z2=1+47i ;
4. а)z1: z2=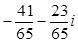 
; б) z1: z2= 
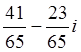; в) z1: z2= 
.
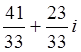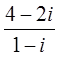3. Составить квадратное уравнение с действительными коэффициентами, если известен один из его корней
х1 =
Ответ: а) x2-6x+10=0; б) x2-6x+8=0; в) x2+6x-10=0
4. Вычислить: 1)i21 ,2) i75 ,3) i44
Ответ: 1) а)i; б)1; в)- i;
2) а)i; б)1; в)- i;
3) а)i; б)1; в)- i.
5. Выполнить действия:
1) (2+5i)2 (3-i);
2)* 
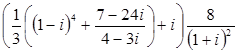
Ответ: 1. а)-43+81i ; б)-83+81i ;в)-23+39i ;
2. а)8i ; б)0; в)-4i .
2.2. Планы-конспекты уроков
План-конспект №1. Тема урока: «Графический способ решения систем уравнений».
Цели урока:
· открыть совместно с учащимися новый способ решения систем уравнений, закрепить навыки построения графиков элементарных функций;
· формировать потребность приобретения новых знаний, создать условия для систематизации (самосистематизации) усвоения умений и навыков;
· развивать математическую речь при комментировании решения;
· воспитывать уважение друг к другу, взаимопонимание, уверенность в себе, развивать самостоятельность и творчество.
Ход урока.
Для урока мы используем следующую литературу: Учебник Ю.Н. Макарычева “Алгебра 9” под редакцией С.А. Теляковского., “Сборник задач для проведения письменного экзамена по алгебре за курс основной школы” “Дрофа” Москва 2001г., Материалы Единого Государственного Экзамена.
Во время урока учащийся ведет лист самосистематизации, где в ходе урока оценивает свое участие по 3-х бальной шкале (0,1,2).
1 – Самоопределение к деятельности. Организационный момент
Эпиграф: Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю (Гёте И.)
Дата: 2019-05-28, просмотров: 202.
