Для определения индекса наблюдаемости системы используется программа Observ.exe. Индекс наблюдаемости используется в программе Luen.exe для определения порядка необходимого корректирующего фильтра.
Индексом наблюдаемости системы называется такое минимальное целое число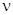 
, при котором матрица 
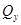, определяемая выражением 
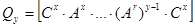, имеет ранг равный 
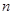. В общем случае 
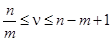. Если ранг 
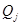равен 
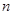, в то время как ранг 
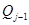меньше 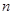, то индекс наблюдаемости 
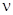равен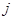 
. Если ранг 
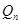меньше 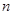, то система считается ненаблюдаемой.
Для расчета индекса наблюдаемости 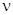необходимо ввести порядок матрицы 
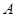и матрицы 
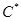. Так как по условию наблюдаемыми состояниями являются 
, 
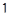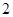и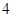 
, то матрица 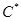будет иметь вид:
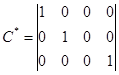. (3.1)
Использовав программу Observ.exe, получим значение индекса наблюдаемости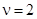 
. Порядок наблюдателя Люенбергера определяется из соотношения:
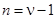. (3.2)
Таким образом, в системе будет использоваться наблюдатель Люенбергера первого порядка, то есть наблюдатель будет состоять из одного интегратора.
Проектирование САУ с заданными свойствами с использованием наблюдателя Люенбергера
Построение структурной схемы САУ с наблюдателем Люенбергера
Используя программу Luen.exe, получим следующие значения параметров, необходимых для построения структурной схемы САУ с наблюдателем Люенбергера:
— собственные значения наблюдателя: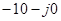 
;
— коэффициенты характеристического полинома: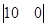 
;
— матрица F: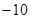 
;
— матрица G1: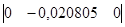 
;
— матрица G2: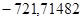 
;
— коэффициенты ОС по выходу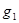 
: 
; 
; 
;
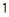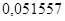— коэффициенты ОС наблюдателя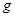 
: .
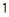Для наблюдателя Люенбергера справедлива следующая система уравнений:
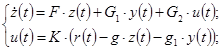(3.3)
Используя систему (3.3), построим структурную схему САУ с наблюдателем Люенбергера (рис. 3.4).
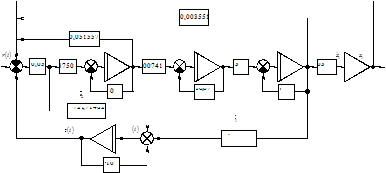
Рисунок 3.4 — Структурная схема САУ с наблюдателем Люенбергера
Оценка качества скорректированной САУ
На основании структурной схемы САУ в пространстве состояний (рис. 3.4) запишем матрицы коэффициентов, входных сигналов на интеграторы и выходных сигналов с интеграторов:
, 
, 
.
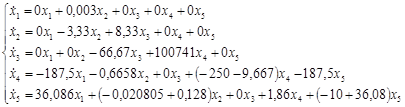
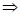
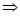
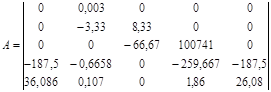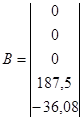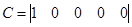Используя программу Stvarfdbk.exe, получим следующую передаточную функцию системы с наблюдателем Люенбергера:
.
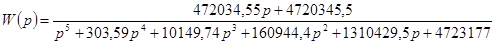С помощью программы Perehod.exe определяем время переходного процесса и перерегулирование:
, 
.
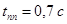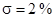Погрешность по времени переходного процесса будет равна:
.
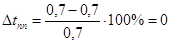Погрешность по перерегулированию:
.
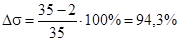График переходного процесса представлен на рисунке 3.5.
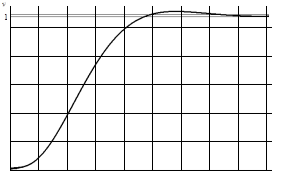
Рисунок 3.5 — Переходной процесс в скорректированной системе
ВЫВОДЫ
В процессе выполнения работы была проанализирована автоматическая система — электропривод постоянного тока. Для нее были выполнены последовательная и параллельная коррекция.
Последовательное корректирующее устройство вводит производную по рассогласованию, что увеличивает запас устойчивости системы и улучшает качество переходных процессов. При реализации этого вида коррекции были достигнуты следующие параметры точности:
, 
.
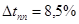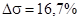Недостатки этого вида коррекции:
— в процессе эксплуатации при изменении параметров последовательных элементов системы, уменьшается эффект коррекции;
— 
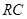-контуры чувствительны к высокочастотным помехам.
Параллельные корректирующие устройства работают при меньшем уровне помех, чем последовательные, так как сигнал поступает на него пройдя в начале через всю систему, являющуюся фильтром низких частот. Благодаря этому эффективность действия параллельного корректирующего устройства при наложении помех на сигнал ошибки снижается в меньшей мере, чем последовательного. Здесь были достигнуты следующие параметры точности:
, 
.
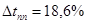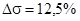Коррекция с помощью обратных связей обладает следующими достоинствами:
— нелинейные свойства элементов, охваченных обратной связью, линеаризуются, так как передаточные свойства охваченного участка определяются параметрами контура в цепи обратной связи.
Вместе с достоинствами есть и недостатки, такие как:
— сложность и большая стоимость их реализации;
— трудности при суммировании сигнала обратной связи и сигнала обратной связи и сигнала ошибки;
— контур обратной связи сам по себе может оказаться неустойчивым.
Последовательная коррекция применяется в маломощных системах, а коррекция с ОС в мощных системах.
Наблюдатель Люенбергера является наилучшим корректирующим устройством, которое приближает переходной процесс к желаемому, но его реализация сложна, так как необходимо выполнить еще одно интегрирующее устройство, а также устройство сложения и сравнения сигналов от различных интеграторов. Этот вид коррекции применяется в тех случаях, когда ОС нельзя поставить во все измеряемые точки.
Наблюдатель Люенбергера по нескольким измеряемым состояниям, после обработки и сравнения данных судит о протекающем технологическом процессе и выдает соответствующие сигналы на регулятор, который корректирует САУ.
ПЕРЕЧЕНЬ ССЫЛОК
1. Зайцев Г. Ф. Теория автоматического управления и регулирования. — К.: "Высшая школа", 1989, — 431с.
2. Юревич Е. И. Теория автоматического управления. Учебник для студентов высших технических учебных заведений. Издание 2-е, переработанное и дополненное —Л.: "Энергия", 1975.
3. Сборник задач по теории автоматического регулирования и управления, под редакцией В. А. Бесекерского, 5-е издание, переработанное. — М.: "Наука", 1978, — 512с.
4. Клюев А. С. Автоматическое регулирование. Издательство 2-е, переработанное и дополненое. — М.: "Энергия", 1973.
5. Солодовников В. В. Основы теории и элементы системы автоматического регулирования. — М.: "Машиностроение", 1985, - 476с.
6. Воронов А. В. Теория автоматического управления. — М.: "Машиностроение", 1977, - 455с.
Дата: 2019-05-28, просмотров: 284.
