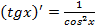
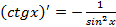
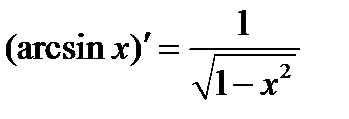
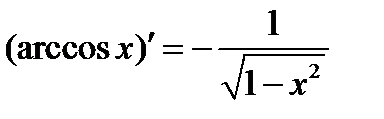
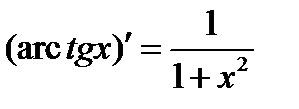
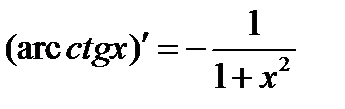
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
Правила вычисления производной
· Производная константы (числа) равна нулю: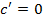 
· 
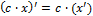, где c – константа
· Производная суммы (разности) равна сумме (разности) производных: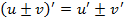 
· Производная произведения: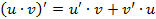 
· Производная отношения: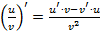 
при 
· Пр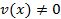оизводная сложной функции: если функция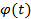 
имеет производную в точке 
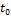, а функция 
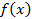имеет производную в точке 
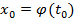, то сложная функция 
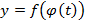имеет производную в точке 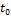, причем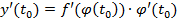 
Пример 3
Найти производную от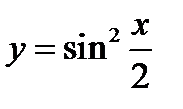 
.
Пример 4
Дана функция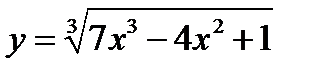 
. Нужно найт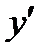и 
и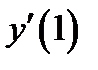 
.
Геометрический смысл производной
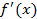в точке 
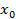равна угловому коэффициенту (тангенсу угла наклона) касательной к графику функции 
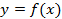в точке 
.
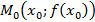Уравнение касательной к кривой 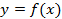в точке :
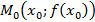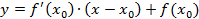
Фактически это уравнение прямой, проходящей через точку 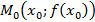и имеющую угловой коэффициент 
.
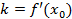Пример 5
В каких точках касательная к графику функции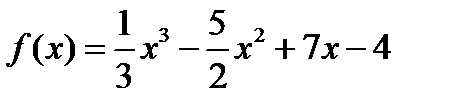 
образует с Ох угол в 45 градусов?
Применение производной для исследования функций и построения эскизов графиков функций
Первая производная
С помощью производной первого порядка (первой производной) мы можем определить экстремумы функции, а также промежутки возрастания и убывания функции.
Если в каждой точке интервала (a, b) f'(x)>0, то функция f(x) возрастает на этом интервале.
Если в каждой точке интервала (a, b) f'(x)<0, то функция f(x) убывает на этом интервале.
Возрастающие или убывающие функции называются монотонными.
Точка х0 называется точкой минимума функции ƒ, если найдется такая окрестность точки х0, что для всех х из этой окрестности справедливо неравенство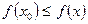 
.
Точка х0 называется точкой максимума функции ƒ, если найдется такая окрестность точки х0, что для всех х из этой окрестности справедливо неравенство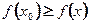 
.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках называются экстремумами функций.
x0 называется критической точкой функции f(x), если
1) x0 – внутренняя точка области определения f(x);
2) f'(x0)=0 или f'(x0) не существует.
Условия существования экстремума
Необходимое условие экстремума:
Если x0 – точка экстремума функции f(x), то эта точка является критической точкой данной функции (критической точкой первого рода).
Достаточное условие экстремума:
Если при переходе через точку x0 производная функции меняет знак, то x0 – точка экстремума функции f(x).
Пример 6
Имеет ли уравнение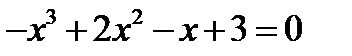 
корни на отрезке [0;2]?
Вторая производная
Вторая производная – или производная второго порядка – это производная от первой производной.
Для понимания смысла этого действия можно привести такой пример:
Пусть у нас есть формула, которой задается преодоленное объектом расстояние s в зависимости от времени t: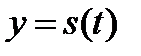 
. Тогда скорость объекта v – это первая производная от у: 
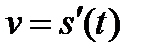. А ускорение а, то есть скорость изменения скорости, - это вторая производная от у: 
.
При исследовании функции с помощью производной второго порядка (второй производной) мы можем определить промежутки выпуклости и вогнутости функции, а также точки перегиба.
График функции называется выпуклым на интервале, если он расположен ниже касательной, проведенной к кривой в любой точке этого интервала
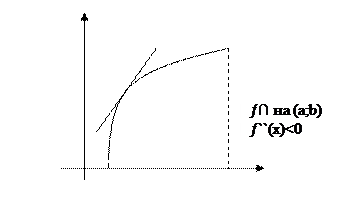
График функции называется вогнутым на интервале, если он расположен выше касательной, проведенной к кривой в любой точке этого интервала
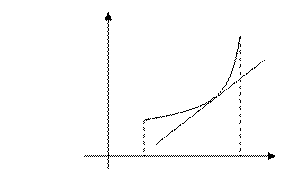
Теорема. Достаточное условие выпуклости (вогнутости) графика функции
Пусть функция дважды дифференцируема на интервале. Если ƒ′′(х) <0 на (a;b), то график функции выпуклый на (a;b); если ƒ′′(х)>0 на (a;b), то график функции вогнутый на (a;b).
Точкой перегиба называется точка графика функции, отделяющая его выпуклую часть от вогнутой, и наоборот.
Дата: 2019-04-23, просмотров: 172.
