Лекция 2-7
Производная
Монотонность, выпуклость. Касательная к графику в точке
Определение производной и ее смысл
Пусть есть тропинка, по которой можно идти то вверх, то вниз, не сворачивая при этом ни вправо, ни влево
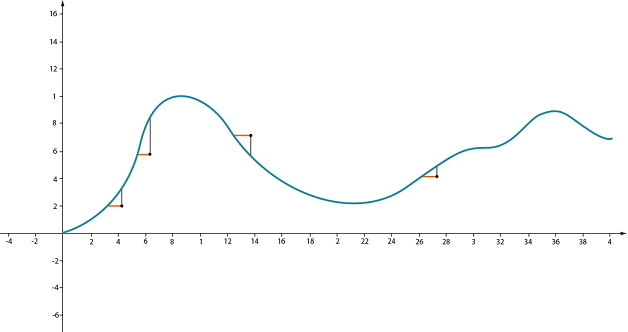
Допустим, мы хотим понять, насколько крутой уклон нас ждет впереди. Чтобы измерить эту крутизну, нужно понять, насколько сильно (круто) увеличивается высота при перемещении вперед на единицу расстояния:
.
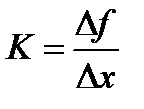Если мы поднимаемся, то K>0, если спускаемся, K<0. Если дорога ровная, без уклона, то K=0.
Возникает вопрос, что взять за единицу расстояния. Если взять слишком большую величину, может оказаться так, что это расстояние включит в себя, например, холм, и мы не поймем, что в процессе уклон будет меняться.
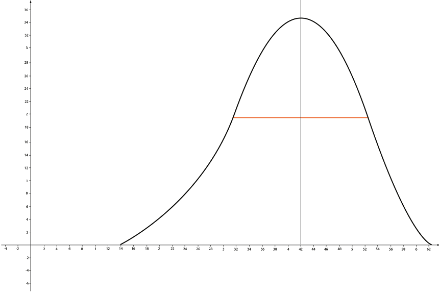
Чтобы не сталкиваться с такой проблемой, в математике берется бесконечно малая величина, то есть в нашем примере крутизна уклона будет измеряться как
.
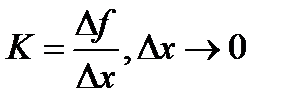Собственно, это и будет производная. Она показывает скорость изменения функции в данной точке.
П роизводная функции – это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю , если такой предел существует.
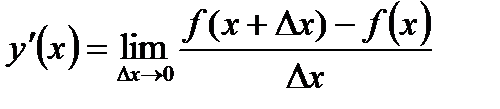
Функцию, имеющую конечную производную в данной точке, называют дифференцируемой в этой точке, а процесс вычисления производной - дифференцированием. Функция дифференцируема на множестве точек (например, на отрезке, интервале или на всей области определения), только если она дифференцируема в каждой точке этого множества.
Пример 1
По определению выведите производную для функции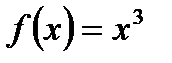 
.
Правой (левой) производной функции f(x) в точке x0 называется предел справа (слева) отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Теорема (1)
Функция имеет производную в точке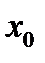 
, если в этой точке существуют и равны между собой производные справа и слева.
При этом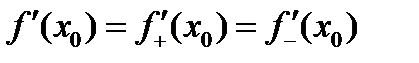 
.
Обратное также верно: если в точке 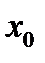существуют и равны между собой производные справа и слева, то функция имеет производную в этой точке.
Функция f(x) называется непрерывной в точке х0, если f(x) имеет предел в точке х0, и этот предел совпадает со значением функции f(x0):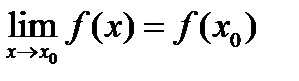 
.
Функция непрерывна на множестве, если она непрерывна в каждой точке этого множества.
График непрерывной функции является непрерывной линией.
Теорема (2)
Если функция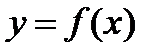 
имеет производную в точке 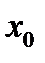, то функция непрерывна в этой точке.
Пример 2
Проверить существование производной функции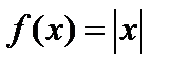 
в точке х=0.
Производные элементарных функций
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
· 
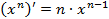
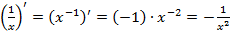
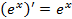
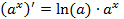
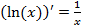
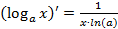
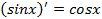
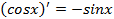
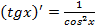
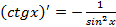
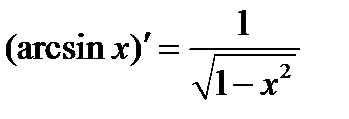
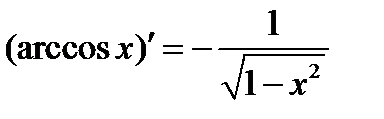
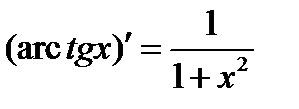
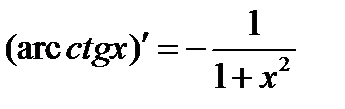
Пример 3
Найти производную от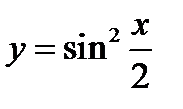 
.
Пример 4
Дана функция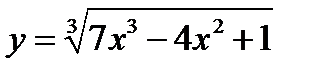 
. Нужно найти 
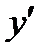и 
.
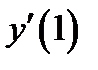Пример 5
В каких точках касательная к графику функции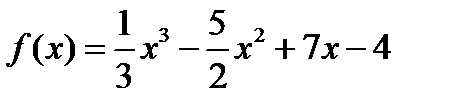 
образует с Ох угол в 45 градусов?
Первая производная
С помощью производной первого порядка (первой производной) мы можем определить экстремумы функции, а также промежутки возрастания и убывания функции.
Если в каждой точке интервала (a, b) f'(x)>0, то функция f(x) возрастает на этом интервале.
Если в каждой точке интервала (a, b) f'(x)<0, то функция f(x) убывает на этом интервале.
Возрастающие или убывающие функции называются монотонными.
Точка х0 называется точкой минимума функции ƒ, если найдется такая окрестность точки х0, что для всех х из этой окрестности справедливо неравенство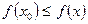 
.
Точка х0 называется точкой максимума функции ƒ, если найдется такая окрестность точки х0, что для всех х из этой окрестности справедливо неравенство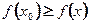 
.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках называются экстремумами функций.
x0 называется критической точкой функции f(x), если
1) x0 – внутренняя точка области определения f(x);
2) f'(x0)=0 или f'(x0) не существует.
Пример 6
Имеет ли уравнение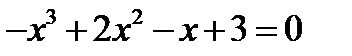 
корни на отрезке [0;2]?
Вторая производная
Вторая производная – или производная второго порядка – это производная от первой производной.
Для понимания смысла этого действия можно привести такой пример:
Пусть у нас есть формула, которой задается преодоленное объектом расстояние s в зависимости от времени t: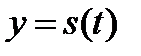 
. Тогда скорость объекта v – это первая производная от у: 
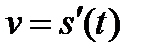. А ускорение а, то есть скорость изменения скорости, - это вторая производная от у: 
.
При исследовании функции с помощью производной второго порядка (второй производной) мы можем определить промежутки выпуклости и вогнутости функции, а также точки перегиба.
График функции называется выпуклым на интервале, если он расположен ниже касательной, проведенной к кривой в любой точке этого интервала
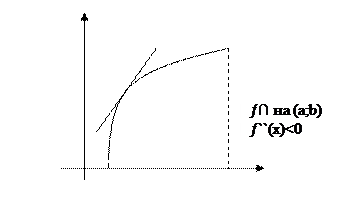
График функции называется вогнутым на интервале, если он расположен выше касательной, проведенной к кривой в любой точке этого интервала
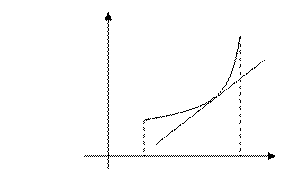
Теорема. Достаточное условие выпуклости (вогнутости) графика функции
Пусть функция дважды дифференцируема на интервале. Если ƒ′′(х) <0 на (a;b), то график функции выпуклый на (a;b); если ƒ′′(х)>0 на (a;b), то график функции вогнутый на (a;b).
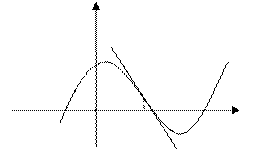
Точкой перегиба называется точка графика функции, отделяющая его выпуклую часть от вогнутой, и наоборот.
Семинар 2-7
Марта 2019
1. По определению выведите производную для функции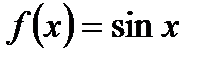 
2. Найти все с, при которых функции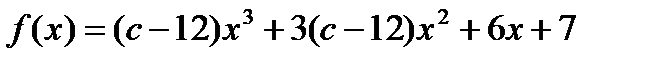 
монотонно возрастает при всех х.
3. Число 18 разбить на два слагаемых так, чтобы сумма их квадратов была наименьшей.
4. Найти площадь треугольника, отсекаемого осями координат и касательной к графику функции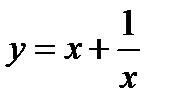 
в точке 
.
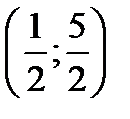5. Найти вторую производную для функции 
.
Домашнее задание 2-7
1. Вычислить:
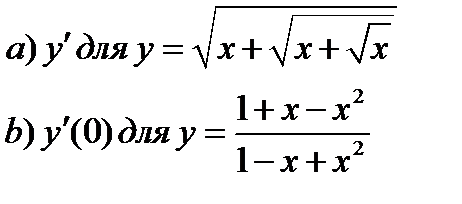
2. Найти точки максимума функции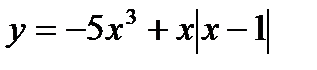 
и ее наименьшее значение на отрезке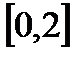 
3. При каких а функция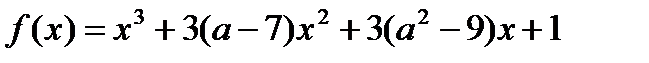 
имеет положительную точку максимума?
4. Прямая касается графика функции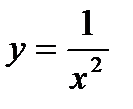 
в точке с абсциссой 
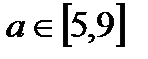. Эта прямая, ось Ох и прямая х=4 ограничивают треугольник. При каких а его площадь будет наибольшей? Найти эту наибольшую площадь.
5. Прямая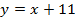 
является касательной к графику функции 
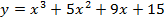. Найдите абсциссу точки касания.
6. Найти наибольшее значение функции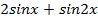 
на отрезке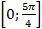 
7. При каких значениях а функция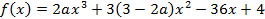 
возрастает на отрезке 
?
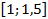8. Вычислить площадь треугольника, ограниченного осями координат и касательной к графику функции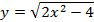 
в точке с абсциссой 
.
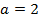9. Найти координаты точек пересечения с осью абсцисс касательных к графику функции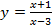 
, которые образуют угол 
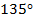с осью ОX.
10. Найти точки перегиба и промежутки выпуклости/вогнутости функции для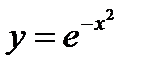 
.
Лекция 2-7
Производная
Монотонность, выпуклость. Касательная к графику в точке
Определение производной и ее смысл
Пусть есть тропинка, по которой можно идти то вверх, то вниз, не сворачивая при этом ни вправо, ни влево
Допустим, мы хотим понять, насколько крутой уклон нас ждет впереди. Чтобы измерить эту крутизну, нужно понять, насколько сильно (круто) увеличивается высота при перемещении вперед на единицу расстояния:
.
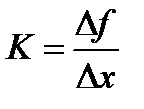Если мы поднимаемся, то K>0, если спускаемся, K<0. Если дорога ровная, без уклона, то K=0.
Возникает вопрос, что взять за единицу расстояния. Если взять слишком большую величину, может оказаться так, что это расстояние включит в себя, например, холм, и мы не поймем, что в процессе уклон будет меняться.
Чтобы не сталкиваться с такой проблемой, в математике берется бесконечно малая величина, то есть в нашем примере крутизна уклона будет измеряться как
.
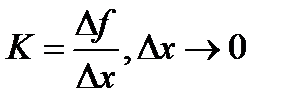Собственно, это и будет производная. Она показывает скорость изменения функции в данной точке.
П роизводная функции – это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю , если такой предел существует.
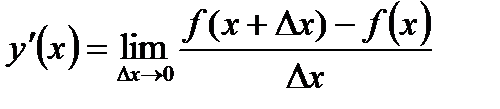
Функцию, имеющую конечную производную в данной точке, называют дифференцируемой в этой точке, а процесс вычисления производной - дифференцированием. Функция дифференцируема на множестве точек (например, на отрезке, интервале или на всей области определения), только если она дифференцируема в каждой точке этого множества.
Пример 1
По определению выведите производную для функции .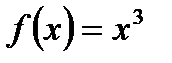
Правой (левой) производной функции f(x) в точке x0 называется предел справа (слева) отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Теорема (1)
Функция имеет производную в точке 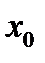, если в этой точке существуют и равны между собой производные справа и слева.
При этом .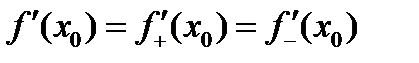
Обратное также верно: если в точке 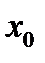существуют и равны между собой производные справа и слева, то функция имеет производную в этой точке.
Функция f(x) называется непрерывной в точке х0, если f(x) имеет предел в точке х0, и этот предел совпадает со значением функции f(x0): .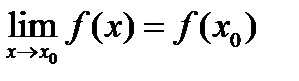
Функция непрерывна на множестве, если она непрерывна в каждой точке этого множества.
График непрерывной функции является непрерывной линией.
Теорема (2)
Если функция 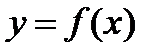имеет производную в точке 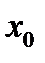, то функция непрерывна в этой точке.
Пример 2
Проверить существование производной функции 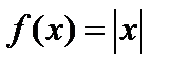в точке х=0.
Дата: 2019-04-23, просмотров: 248.
