Контрольная работа
для студентов 2 курса заочного отделения
Правила выбора варианта контрольного задания, оформления и зачета контрольных работ
1. Контрольная работа должна быть оформлена в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
2. Контрольную работу следует выполнять в обыкновенной ученической тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
3. На обложке тетради должны быть разборчиво написаны фамилия, имя, отчество студента, номер варианта, название дисциплины (Математика). В конце работы следует поставить дату ее выполнения и расписаться.
4. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
5. Номер варианта выполняемого задания совпадает с порядковым номером студента в списке группы. Например, вариант № 4 содержит задания 1.4, 2.4, 3.4, 4.4, 5.4. Решение задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач.
6. Решения задач необходимо оформлять аккуратно, подробно объясняя все действия и используемые формулы, а также делая необходимые чертежи.
7. Срок проверки работ - 7 дней. Студенты обязаны сдавать письменные работы не позже, чем за неделю до экзамена.
8. Зачтенная контрольная работа остается в учебном отделе. Не зачтенная контрольная работа возвращается студенту на доработку. После получения прорецензированной не зачтенной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, выполнить все его рекомендации и сдать повторно.
При выполнении контрольной работы необходимо пользоваться методическим пособием, лекциями, а также др. литературой.
Интернет источники:
1. Интегрирование иррациональных функций http://www.mathprofi.ru/integrirovanie_kornei.html
2. Интегрирование тригонометрических функций http://www.mathprofi.ru/integraly_ot_trigonometricheskih_funkcij.html
2. Интегрирование дробно-рациональной функции http://www.mathprofi.ru/integraly_ot_drobno_racionalnoj_funkcii.html
3. Криволинейные интегралы http://www.mathprofi.ru/krivolineinye_integraly.html
4. Несобственные интегралы http://www.mathprofi.ru/nesobstvennye_integraly.html
5. Ряды Фурье http://www.mathprofi.ru/ryady_furie_primery_reshenij.html
6. Ряд Тейлора. Ряд Маклорена. http://www.mathprofi.ru/razlozhenie_funkcij_v_stepennye_ryady.html
7. Неоднородное дифференциальное уравнение второго порядка http://www.mathprofi.ru/kak_reshit_neodnorodnoe_uravnenie_vtorogo_poryadka.html
Вычислить интеграл
а) 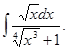 б)
б) 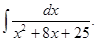
Вычислить интеграл
а) 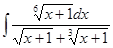 . б)
. б) 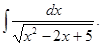
Вычислить интеграл
а) 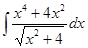 б)
б) 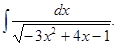
Вычислить интеграл
а) 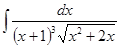 б)
б) 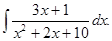
Вычислить интеграл
а) 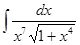 б)
б) 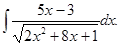
Вычислить интеграл
а) 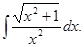 б)
б) 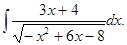
Вычислить интеграл
а) 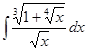 б)
б) 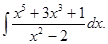
Вычислить интеграл
а) 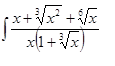 б)
б) 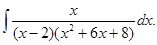
Вычислить интеграл
а) 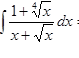 б)
б) 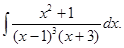
Вычислить интеграл
а) 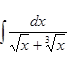 б)
б) 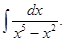
Вычислить интеграл
а) 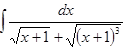 б)
б) 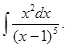
Вычислить интеграл
а) 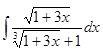 б)
б) 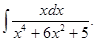
Вычислить интеграл
а) 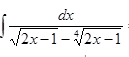 б)
б) 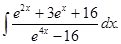
Вычислить интеграл
а) 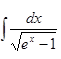 б)
б) 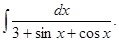
Вычислить интеграл
а) 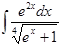 б)
б) 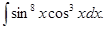
Вычислить интеграл
а) 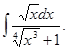 б)
б) 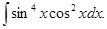
Вычислить интеграл
а) 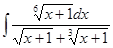 . б)
. б) 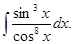
Вычислить интеграл
а) 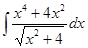 б)
б) 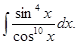
Вычислить интеграл
а) 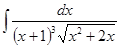 б)
б) 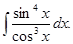
Вычислить интеграл
а) 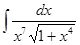 б)
б) 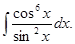
Вычислить интеграл
а) 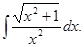 б)
б) 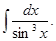
Вычислить интеграл
а) 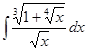 б)
б) 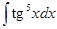
Вычислить интеграл
а) 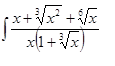 б)
б) 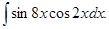
Вычислить интеграл
а) 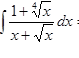 б)
б) 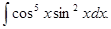
Вычислить интеграл
а) 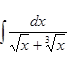 б)
б) 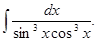
Вычислить интеграл
а) 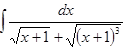 б)
б) 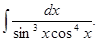
Вычислить интеграл
а) 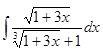 б)
б) 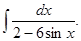
Вычислить интеграл
а) 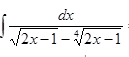 б)
б) 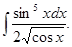
Вычислить интеграл
а) 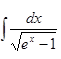 б)
б) 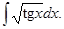
Вычислить интеграл
а) 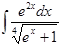 б)
б) 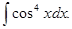
Вычислить интеграл
а) 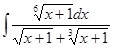 . б)
. б) 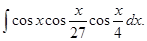
Вычислить интеграл
а) 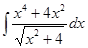 б)
б) 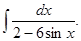
Вычислить интеграл
а) 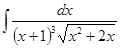 б)
б) 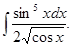
Вычислить интеграл
а) 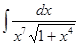 б)
б) 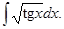
Вычислить интеграл
а) 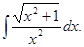 б)
б) 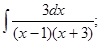
Вычислить интеграл
а) 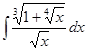 б)
б) 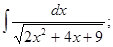
Вычислить интеграл
а) 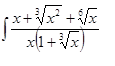 б)
б) 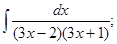
Вычислить интеграл
а) 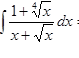 б)
б) 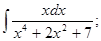
Вычислить интеграл
а) 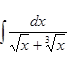 б)
б) 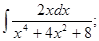
Вычислить интеграл
а) 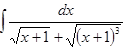 б)
б) 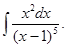
Вычислить интеграл
а) 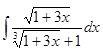 б)
б) 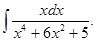
Вычислить интеграл
а) 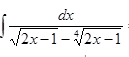 б)
б) 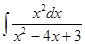
Вычислить интеграл
а) 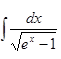 б)
б) 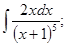
Вычислить интеграл
а) 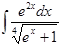 б)
б) 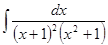
Вычислить интеграл
а) 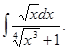 б)
б) 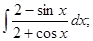
Вычислить интеграл
а) 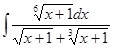 . б)
. б) 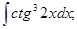
Решить задачу
а) Вычислить криволинейный интеграл
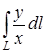 по кривой
по кривой 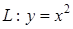 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать на сходимость 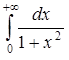
Решить задачу
а) Вычислить криволинейный интеграл
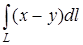 ,
,
где L − отрезок прямой от точки A(0; 0) до точки B(4; 3).
б) Вычислить несобственный интеграл 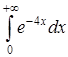 .
.
Решить задачу
а) Найти массу m четверти окружности L радиуса а, расположенной в первом квадранте, если 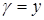 (центр окружности совпадает с началом координат).
(центр окружности совпадает с началом координат).
б) Вычислить несобственный интеграл 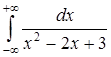 .
.
Решить задачу
а) Вычислить криволинейный интеграл 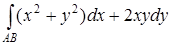 вдоль дуги кубической параболы
вдоль дуги кубической параболы 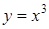 от точки А(1; 1) до В(2; 8).
от точки А(1; 1) до В(2; 8).
б) Исследовать сходимость несобственного интеграла 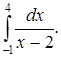
Решить задачу
а) Вычислить криволинейный интеграл 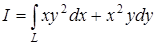 вдоль кривой
вдоль кривой 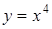 от точки А(1; 1) до точки В(2; 16).
от точки А(1; 1) до точки В(2; 16).
б) Исследовать сходимость несобственного интеграла 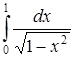 .
.
Решить задачу
а) Вычислить криволинейный интеграл
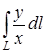 по кривой
по кривой 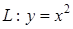 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать сходимость несобственного интеграла
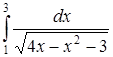 .
.
Решить задачу
а) Вычислить интеграл 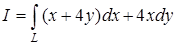 вдоль верхней половины окружности
вдоль верхней половины окружности 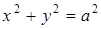 от точки А(-1; 0) до точки В(0; 1).
от точки А(-1; 0) до точки В(0; 1).
б) Вычислить несобственный интеграл 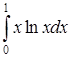 или установить его расходимость.
или установить его расходимость.
Решить задачу
а) Применяя формулу Грина, вычислить 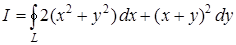 , если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
, если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
б) Определить, сходится ли интеграл 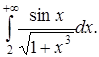
Решить задачу
а) Применяя формулу Грина, вычислить интеграл 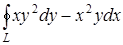 , где L – окружность
, где L – окружность 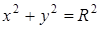 , пробегаемая против хода часовой стрелки.
, пробегаемая против хода часовой стрелки.
б) Исследовать на сходимость интеграл 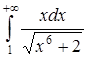 .
.
Решить задачу
а) Выяснить, зависит ли интеграл 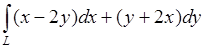 от контура интегрирования.
от контура интегрирования.
б) Исследовать на сходимость 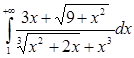 .
.
Решить задачу
а) Вычислить площадь фигуры, ограниченной кривыми у = х2, х = у2, 8ху = 1, примыкающую к началу координат.
б) Исследовать на сходимость интеграл 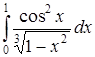 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла: 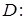
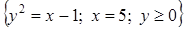 ;
;
б) Вычислить несобственный интеграл 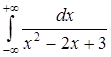 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла 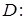
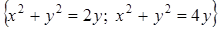 .
.
б) Исследовать на сходимость интеграл 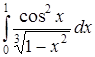 .
.
Решить задачу
а) Вычислить объем пространственного тела V, ограниченного поверхностями
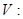
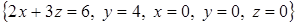 .
.
б) Исследовать на сходимость интеграл
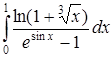 .
.
Решить задачу
а) Вычислить криволинейный интеграл
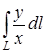 по кривой
по кривой 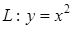 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать на сходимость 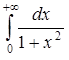
Решить задачу
а) Вычислить криволинейный интеграл
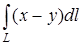 , где L − отрезок прямой от точки A(0; 0) до точки B(4; 3).
, где L − отрезок прямой от точки A(0; 0) до точки B(4; 3).
б) Вычислить несобственный интеграл 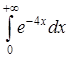 .
.
Решить задачу
а) Найти массу m четверти окружности L радиуса а, расположенной в первом квадранте, если 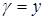 (центр окружности совпадает с началом координат).
(центр окружности совпадает с началом координат).
б) Вычислить несобственный интеграл 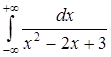 .
.
Решить задачу
а) Вычислить криволинейный интеграл 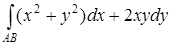 вдоль дуги кубической параболы
вдоль дуги кубической параболы 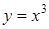 от точки А(1; 1) до В(2; 8).
от точки А(1; 1) до В(2; 8).
б) Исследовать сходимость несобственного интеграла 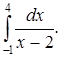
Решить задачу
а) Вычислить криволинейный интеграл 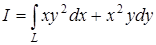 вдоль кривой
вдоль кривой 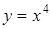 от точки А(1; 1) до точки В(2; 16).
от точки А(1; 1) до точки В(2; 16).
б) Исследовать сходимость несобственного интеграла 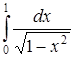 .
.
Решить задачу
а) Вычислить криволинейный интеграл
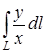 по кривой
по кривой 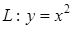 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать сходимость несобственного интеграла
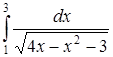 .
.
Решить задачу
а) Вычислить интеграл 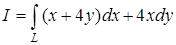 вдоль верхней половины окружности
вдоль верхней половины окружности 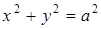 от точки А(-1; 0) до точки В(0; 1).
от точки А(-1; 0) до точки В(0; 1).
б) Вычислить несобственный интеграл 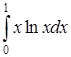 или установить его расходимость.
или установить его расходимость.
Решить задачу
а) Применяя формулу Грина, вычислить 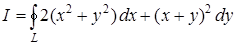 , если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
, если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
б) Определить, сходится ли интеграл 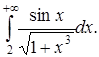
Решить задачу
а) Применяя формулу Грина, вычислить интеграл 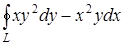 , где L – окружность
, где L – окружность 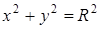 , пробегаемая против хода часовой стрелки.
, пробегаемая против хода часовой стрелки.
б) Исследовать на сходимость интеграл 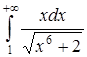 .
.
Решить задачу
а) Выяснить, зависит ли интеграл 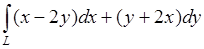 от контура интегрирования.
от контура интегрирования.
б) Исследовать на сходимость 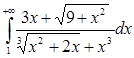 .
.
Решить задачу
а) Вычислить площадь фигуры, ограниченной кривыми у = х2, х = у2, 8ху = 1, примыкающую к началу координат.
б) Исследовать на сходимость интеграл 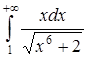
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла: 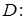
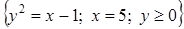 ;
;
б) Определить, сходится ли интеграл 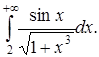
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла 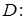
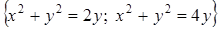 .
.
б) Исследовать на сходимость интеграл 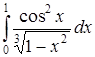 .
.
Решить задачу
а) Вычислить объем пространственного тела V, ограниченного поверхностями
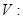
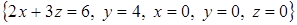 .
.
б) Исследовать на сходимость интеграл
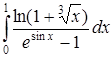 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла 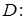
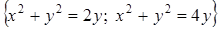 .
.
б) Исследовать на сходимость интеграл 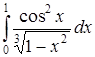 .
.
Решить задачу
а) Вычислить объем пространственного тела V, ограниченного поверхностями
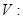
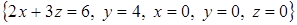 .
.
б) Исследовать на сходимость интеграл
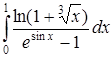 .
.
Решить задачу
а) Вычислить повторный интеграл: 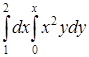
б) Вычислить несобственный интеграл 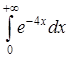 .
.
Решить задачу
а) Вычислить повторный интеграл: 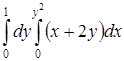 .
.
б) Вычислить несобственный интеграл 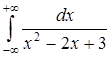 .
.
Решить задачу
а) Вычислить 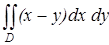 , если область D ограничена линиями
, если область D ограничена линиями 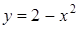 ,
, 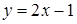 .
.
б) Исследовать сходимость несобственного интеграла 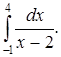
Решить задачу
а) Вычислить интеграл 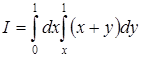 .
.
б) Исследовать сходимость несобственного интеграла 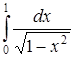 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла, если 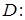
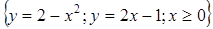 .
.
б) Исследовать сходимость несобственного интеграла
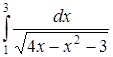 .
.
Решить задачу
а) Вычислить длину дуги циклоиды 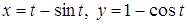
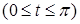
б) Вычислить несобственный интеграл 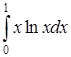 или установить его расходимость.
или установить его расходимость.
Решить задачу
а) Вычислить площадь поверхности цилиндра 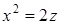 , отсеченной плоскостями
, отсеченной плоскостями 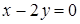 ,
, 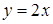 ,
, 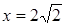 .
.
б) Определить, сходится ли интеграл 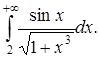
Решить задачу
а) Найти площадь части конуса 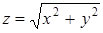 , заключенной внутри цилиндра
, заключенной внутри цилиндра 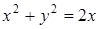 .
.
б) Исследовать на сходимость интеграл 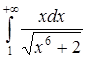 .
.
Решить задачу
а) Будет ли криволинейный интеграл
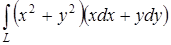
равен нулю по любому замкнутому контуру?
б) Исследовать на сходимость 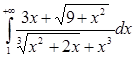 .
.
Решить задачу
а) Применяя формулу Грина, вычислить интеграл 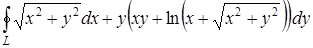 , где L – контур прямоугольника
, где L – контур прямоугольника 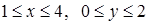 .
.
б) Исследовать на сходимость интеграл 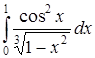 .
.
Решить задачу
а) Выяснить, зависит ли интеграл 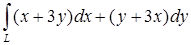 от контура интегрирования.
от контура интегрирования.
б) Вычислить несобственный интеграл 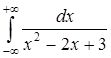 .
.
Решить задачу
а) Вычислить площадь фигуры, ограниченную эллипсом 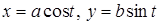 .
.
б) Исследовать на сходимость интеграл 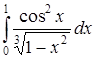 .
.
Решить задачу
а) Вычислите криволинейный интеграл:
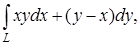 где L – дуга параболы
где L – дуга параболы 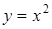 от А(-1; 1) до В(-2; 4);
от А(-1; 1) до В(-2; 4);
б) Исследовать на сходимость интеграл
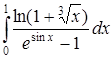 .
.
Решить задачу
а) Вычислите криволинейный интеграл:
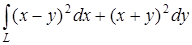 вдоль ломаной, соединяющей точки О(0; 0), А(2; 0) и В(4; 2);
вдоль ломаной, соединяющей точки О(0; 0), А(2; 0) и В(4; 2);
б) Исследовать на сходимость 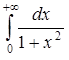
Решить задачу
а) Вычислить криволинейный интеграл
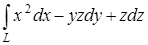 вдоль прямой, соединяющей точки А(1; 2; -−1) и В(3; 3; 2).
вдоль прямой, соединяющей точки А(1; 2; -−1) и В(3; 3; 2).
б) Вычислить несобственный интеграл 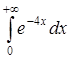 .
.
Решить задачу
а) Вычислите криволинейный интеграл:
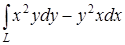 , если
, если 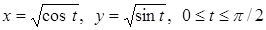 ;б) Вычислить несобственный интеграл
;б) Вычислить несобственный интеграл 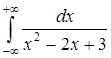 .
.
Контрольная работа
для студентов 2 курса заочного отделения
Правила выбора варианта контрольного задания, оформления и зачета контрольных работ
1. Контрольная работа должна быть оформлена в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
2. Контрольную работу следует выполнять в обыкновенной ученической тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
3. На обложке тетради должны быть разборчиво написаны фамилия, имя, отчество студента, номер варианта, название дисциплины (Математика). В конце работы следует поставить дату ее выполнения и расписаться.
4. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
5. Номер варианта выполняемого задания совпадает с порядковым номером студента в списке группы. Например, вариант № 4 содержит задания 1.4, 2.4, 3.4, 4.4, 5.4. Решение задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач.
6. Решения задач необходимо оформлять аккуратно, подробно объясняя все действия и используемые формулы, а также делая необходимые чертежи.
7. Срок проверки работ - 7 дней. Студенты обязаны сдавать письменные работы не позже, чем за неделю до экзамена.
8. Зачтенная контрольная работа остается в учебном отделе. Не зачтенная контрольная работа возвращается студенту на доработку. После получения прорецензированной не зачтенной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, выполнить все его рекомендации и сдать повторно.
При выполнении контрольной работы необходимо пользоваться методическим пособием, лекциями, а также др. литературой.
Интернет источники:
1. Интегрирование иррациональных функций http://www.mathprofi.ru/integrirovanie_kornei.html
2. Интегрирование тригонометрических функций http://www.mathprofi.ru/integraly_ot_trigonometricheskih_funkcij.html
2. Интегрирование дробно-рациональной функции http://www.mathprofi.ru/integraly_ot_drobno_racionalnoj_funkcii.html
3. Криволинейные интегралы http://www.mathprofi.ru/krivolineinye_integraly.html
4. Несобственные интегралы http://www.mathprofi.ru/nesobstvennye_integraly.html
5. Ряды Фурье http://www.mathprofi.ru/ryady_furie_primery_reshenij.html
6. Ряд Тейлора. Ряд Маклорена. http://www.mathprofi.ru/razlozhenie_funkcij_v_stepennye_ryady.html
7. Неоднородное дифференциальное уравнение второго порядка http://www.mathprofi.ru/kak_reshit_neodnorodnoe_uravnenie_vtorogo_poryadka.html
Вычислить интеграл
а) 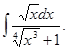 б)
б) 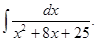
Вычислить интеграл
а) 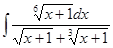 . б)
. б) 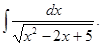
Вычислить интеграл
а) 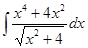 б)
б) 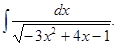
Вычислить интеграл
а) 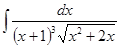 б)
б) 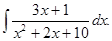
Вычислить интеграл
а) 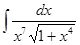 б)
б) 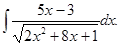
Вычислить интеграл
а) 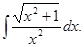 б)
б) 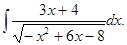
Вычислить интеграл
а) 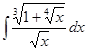 б)
б) 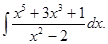
Вычислить интеграл
а) 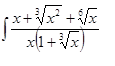 б)
б) 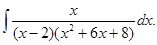
Вычислить интеграл
а) 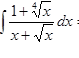 б)
б) 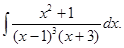
Вычислить интеграл
а) 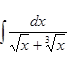 б)
б) 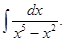
Вычислить интеграл
а) 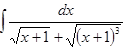 б)
б) 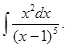
Вычислить интеграл
а) 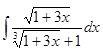 б)
б) 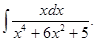
Вычислить интеграл
а) 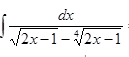 б)
б) 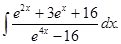
Вычислить интеграл
а) 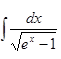 б)
б) 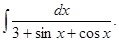
Вычислить интеграл
а) 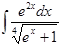 б)
б) 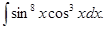
Вычислить интеграл
а) 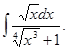 б)
б) 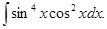
Вычислить интеграл
а) 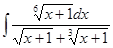 . б)
. б) 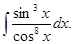
Вычислить интеграл
а) 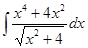 б)
б) 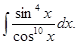
Вычислить интеграл
а) 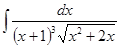 б)
б) 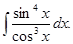
Вычислить интеграл
а) 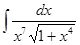 б)
б) 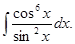
Вычислить интеграл
а) 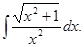 б)
б) 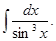
Вычислить интеграл
а) 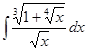 б)
б) 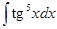
Вычислить интеграл
а) 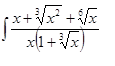 б)
б) 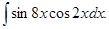
Вычислить интеграл
а) 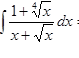 б)
б) 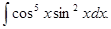
Вычислить интеграл
а) 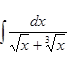 б)
б) 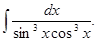
Вычислить интеграл
а) 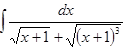 б)
б) 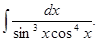
Вычислить интеграл
а) 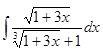 б)
б) 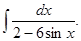
Вычислить интеграл
а) 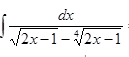 б)
б) 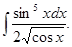
Вычислить интеграл
а) 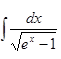 б)
б) 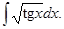
Вычислить интеграл
а) 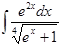 б)
б) 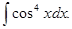
Вычислить интеграл
а) 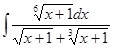 . б)
. б) 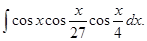
Вычислить интеграл
а) 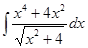 б)
б) 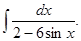
Вычислить интеграл
а) 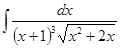 б)
б) 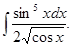
Вычислить интеграл
а) 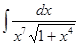 б)
б) 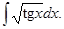
Вычислить интеграл
а) 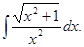 б)
б) 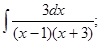
Вычислить интеграл
а) 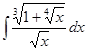 б)
б) 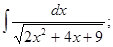
Вычислить интеграл
а) 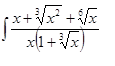 б)
б) 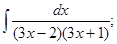
Вычислить интеграл
а) 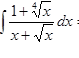 б)
б) 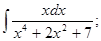
Вычислить интеграл
а) 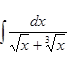 б)
б) 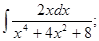
Вычислить интеграл
а) 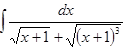 б)
б) 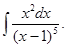
Вычислить интеграл
а) 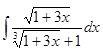 б)
б) 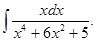
Вычислить интеграл
а) 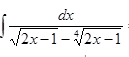 б)
б) 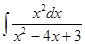
Вычислить интеграл
а) 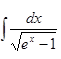 б)
б) 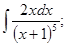
Вычислить интеграл
а) 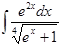 б)
б) 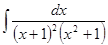
Вычислить интеграл
а) 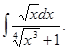 б)
б) 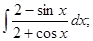
Вычислить интеграл
а) 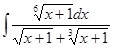 . б)
. б) 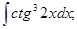
Решить задачу
а) Вычислить криволинейный интеграл
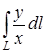 по кривой
по кривой 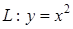 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать на сходимость 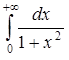
Решить задачу
а) Вычислить криволинейный интеграл
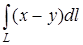 ,
,
где L − отрезок прямой от точки A(0; 0) до точки B(4; 3).
б) Вычислить несобственный интеграл 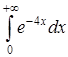 .
.
Решить задачу
а) Найти массу m четверти окружности L радиуса а, расположенной в первом квадранте, если 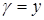 (центр окружности совпадает с началом координат).
(центр окружности совпадает с началом координат).
б) Вычислить несобственный интеграл 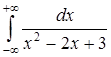 .
.
Решить задачу
а) Вычислить криволинейный интеграл 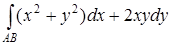 вдоль дуги кубической параболы
вдоль дуги кубической параболы 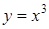 от точки А(1; 1) до В(2; 8).
от точки А(1; 1) до В(2; 8).
б) Исследовать сходимость несобственного интеграла 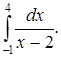
Решить задачу
а) Вычислить криволинейный интеграл 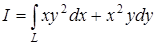 вдоль кривой
вдоль кривой 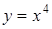 от точки А(1; 1) до точки В(2; 16).
от точки А(1; 1) до точки В(2; 16).
б) Исследовать сходимость несобственного интеграла 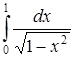 .
.
Решить задачу
а) Вычислить криволинейный интеграл
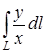 по кривой
по кривой 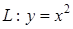 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать сходимость несобственного интеграла
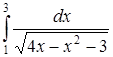 .
.
Решить задачу
а) Вычислить интеграл 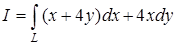 вдоль верхней половины окружности
вдоль верхней половины окружности 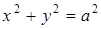 от точки А(-1; 0) до точки В(0; 1).
от точки А(-1; 0) до точки В(0; 1).
б) Вычислить несобственный интеграл 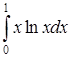 или установить его расходимость.
или установить его расходимость.
Решить задачу
а) Применяя формулу Грина, вычислить 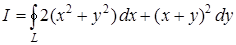 , если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
, если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
б) Определить, сходится ли интеграл 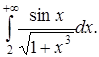
Решить задачу
а) Применяя формулу Грина, вычислить интеграл 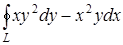 , где L – окружность
, где L – окружность 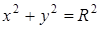 , пробегаемая против хода часовой стрелки.
, пробегаемая против хода часовой стрелки.
б) Исследовать на сходимость интеграл 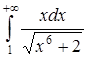 .
.
Решить задачу
а) Выяснить, зависит ли интеграл 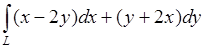 от контура интегрирования.
от контура интегрирования.
б) Исследовать на сходимость 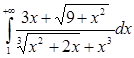 .
.
Решить задачу
а) Вычислить площадь фигуры, ограниченной кривыми у = х2, х = у2, 8ху = 1, примыкающую к началу координат.
б) Исследовать на сходимость интеграл 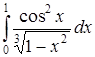 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла: 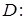
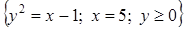 ;
;
б) Вычислить несобственный интеграл 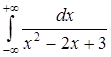 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла 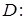
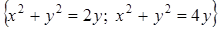 .
.
б) Исследовать на сходимость интеграл 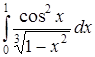 .
.
Решить задачу
а) Вычислить объем пространственного тела V, ограниченного поверхностями
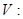
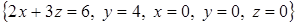 .
.
б) Исследовать на сходимость интеграл
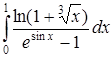 .
.
Решить задачу
а) Вычислить криволинейный интеграл
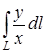 по кривой
по кривой 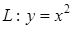 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать на сходимость 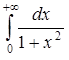
Решить задачу
а) Вычислить криволинейный интеграл
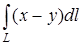 , где L − отрезок прямой от точки A(0; 0) до точки B(4; 3).
, где L − отрезок прямой от точки A(0; 0) до точки B(4; 3).
б) Вычислить несобственный интеграл 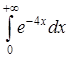 .
.
Решить задачу
а) Найти массу m четверти окружности L радиуса а, расположенной в первом квадранте, если 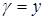 (центр окружности совпадает с началом координат).
(центр окружности совпадает с началом координат).
б) Вычислить несобственный интеграл 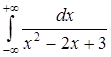 .
.
Решить задачу
а) Вычислить криволинейный интеграл 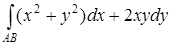 вдоль дуги кубической параболы
вдоль дуги кубической параболы 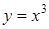 от точки А(1; 1) до В(2; 8).
от точки А(1; 1) до В(2; 8).
б) Исследовать сходимость несобственного интеграла 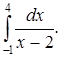
Решить задачу
а) Вычислить криволинейный интеграл 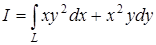 вдоль кривой
вдоль кривой 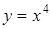 от точки А(1; 1) до точки В(2; 16).
от точки А(1; 1) до точки В(2; 16).
б) Исследовать сходимость несобственного интеграла 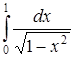 .
.
Решить задачу
а) Вычислить криволинейный интеграл
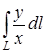 по кривой
по кривой 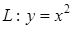 от начала координат до точки с абсциссой х = 2.
от начала координат до точки с абсциссой х = 2.
б) Исследовать сходимость несобственного интеграла
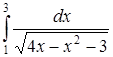 .
.
Решить задачу
а) Вычислить интеграл 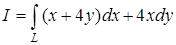 вдоль верхней половины окружности
вдоль верхней половины окружности 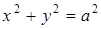 от точки А(-1; 0) до точки В(0; 1).
от точки А(-1; 0) до точки В(0; 1).
б) Вычислить несобственный интеграл 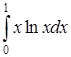 или установить его расходимость.
или установить его расходимость.
Решить задачу
а) Применяя формулу Грина, вычислить 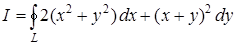 , если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
, если L – контур треугольника с вершинами А(1; 1), В(2; 2), С(1; 3), пробегаемый против хода часовой стрелки.
б) Определить, сходится ли интеграл 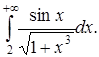
Решить задачу
а) Применяя формулу Грина, вычислить интеграл 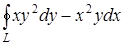 , где L – окружность
, где L – окружность 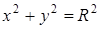 , пробегаемая против хода часовой стрелки.
, пробегаемая против хода часовой стрелки.
б) Исследовать на сходимость интеграл 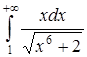 .
.
Решить задачу
а) Выяснить, зависит ли интеграл 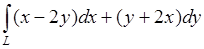 от контура интегрирования.
от контура интегрирования.
б) Исследовать на сходимость 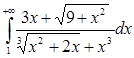 .
.
Решить задачу
а) Вычислить площадь фигуры, ограниченной кривыми у = х2, х = у2, 8ху = 1, примыкающую к началу координат.
б) Исследовать на сходимость интеграл 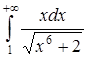
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла: 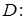
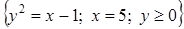 ;
;
б) Определить, сходится ли интеграл 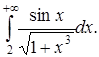
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла 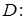
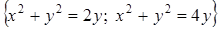 .
.
б) Исследовать на сходимость интеграл 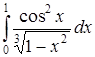 .
.
Решить задачу
а) Вычислить объем пространственного тела V, ограниченного поверхностями
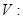
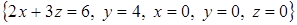 .
.
б) Исследовать на сходимость интеграл
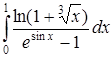 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла 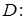
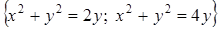 .
.
б) Исследовать на сходимость интеграл 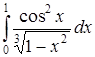 .
.
Решить задачу
а) Вычислить объем пространственного тела V, ограниченного поверхностями
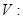
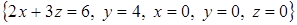 .
.
б) Исследовать на сходимость интеграл
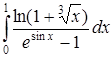 .
.
Решить задачу
а) Вычислить повторный интеграл: 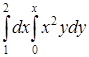
б) Вычислить несобственный интеграл 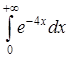 .
.
Решить задачу
а) Вычислить повторный интеграл: 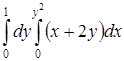 .
.
б) Вычислить несобственный интеграл 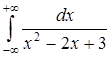 .
.
Решить задачу
а) Вычислить 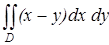 , если область D ограничена линиями
, если область D ограничена линиями 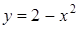 ,
, 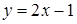 .
.
б) Исследовать сходимость несобственного интеграла 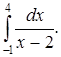
Решить задачу
а) Вычислить интеграл 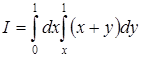 .
.
б) Исследовать сходимость несобственного интеграла 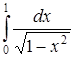 .
.
Решить задачу
а) Вычислить площадь плоской фигуры D с помощью двойного интеграла, если 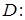
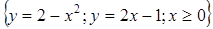 .
.
б) Исследовать сходимость несобственного интеграла
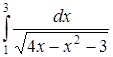 .
.
Решить задачу
а) Вычислить длину дуги циклоиды 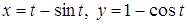
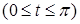
б) Вычислить несобственный интеграл 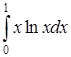 или установить его расходимость.
или установить его расходимость.
Решить задачу
а) Вычислить площадь поверхности цилиндра 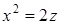 , отсеченной плоскостями
, отсеченной плоскостями 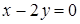 ,
, 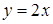 ,
, 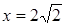 .
.
б) Определить, сходится ли интеграл 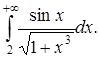
Решить задачу
а) Найти площадь части конуса 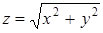 , заключенной внутри цилиндра
, заключенной внутри цилиндра 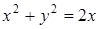 .
.
б) Исследовать на сходимость интеграл 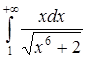 .
.
Решить задачу
а) Будет ли криволинейный интеграл
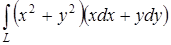
равен нулю по любому замкнутому контуру?
б) Исследовать на сходимость 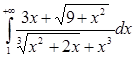 .
.
Решить задачу
а) Применяя формулу Грина, вычислить интеграл 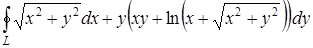 , где L – контур прямоугольника
, где L – контур прямоугольника 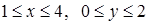 .
.
б) Исследовать на сходимость интеграл 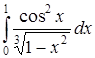 .
.
Решить задачу
а) Выяснить, зависит ли интеграл 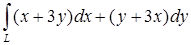 от контура интегрирования.
от контура интегрирования.
б) Вычислить несобственный интеграл 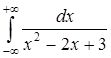 .
.
Решить задачу
а) Вычислить площадь фигуры, ограниченную эллипсом 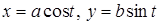 .
.
б) Исследовать на сходимость интеграл 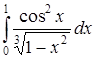 .
.
Решить задачу
а) Вычислите криволинейный интеграл:
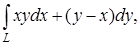 где L – дуга параболы
где L – дуга параболы 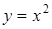 от А(-1; 1) до В(-2; 4);
от А(-1; 1) до В(-2; 4);
б) Исследовать на сходимость интеграл
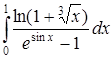 .
.
Решить задачу
а) Вычислите криволинейный интеграл:
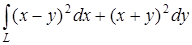 вдоль ломаной, соединяющей точки О(0; 0), А(2; 0) и В(4; 2);
вдоль ломаной, соединяющей точки О(0; 0), А(2; 0) и В(4; 2);
б) Исследовать на сходимость 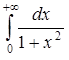
Решить задачу
а) Вычислить криволинейный интеграл
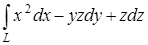 вдоль прямой, соединяющей точки А(1; 2; -−1) и В(3; 3; 2).
вдоль прямой, соединяющей точки А(1; 2; -−1) и В(3; 3; 2).
б) Вычислить несобственный интеграл 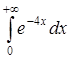 .
.
Решить задачу
а) Вычислите криволинейный интеграл:
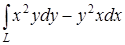 , если
, если 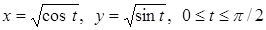 ;б) Вычислить несобственный интеграл
;б) Вычислить несобственный интеграл 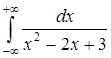 .
.
Исследовать сходимость рядов
а) 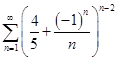
б) Установить равномерную сходимость ряда 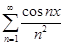 на любом отрезке.
на любом отрезке.
Дата: 2019-05-28, просмотров: 278.