Цели:
· проверить знания учащихся по теме: «Квадратные уравнения»;
· продолжить подготовку учащихся к экзаменам;
· развивать математическую речь, память, самостоятельность;
· воспитывать трудолюбие, усидчивость.
Оборудование: карточки с заданиями
План урока
1. Повторение определений.
2. Решение теста.
3. Повторение формул, терминологический диктант.
4. Решение контрольной работы.
Организационный момент
Сегодня на уроке мы проверим ваши знания по теме: «Квадратные уравнения». Наша работа будет состоять из: повторения определений, решения теста, повторения формул, терминологического диктанта, решения контрольной работы.
Каждому учащемуся выдаются карточки с заданиями.
Задание 1. Повторение определений.
На 2 варианта раздаются карточки.
Определения для первого варианта.
1. Определение квадратного уравнения.
2. Определение полного, неполного квадратного уравнения.
3. Что, значит, решить квадратное уравнение.
Определения для второго варианта.
1. Определение приведенного, неприведенного квадратного уравнения.
2. Определение корней квадратного уравнения.
3. Алгоритм решения квадратного уравнения.
Задание 2. Решение теста.
Тест.
1 в.
1) Выберите приведенное квадратное уравнение из данных:
а) x2-1+x=0; в) x-2x2+2=0
б) 3x-2x2+1=0; г) x2-2=0.
2) Какое из чисел является корнем уравнения 2x2-3x-14=0?
а) 3; б) -2; в) 2; г) -3.
3) Решите уравнение x2-36=0.
а) 6 и 0; б) 6 и -6; в) 0 и -6; г) 6.
4) Сколько корней имеет уравнение x2+10x+25=0?
а) множество; б) один; в) два; г) ни одного.
5) Решите уравнение 6x2+7x+2=0.
а) 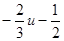 ; б)
; б) 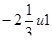 ; в)
; в)  ; г)
; г) 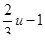 .
.
6) Укажите в квадратном уравнении 4x-3x2+7=0 его коэффициенты:
а) a=4, b=3, c=7; в) a=-3, b=4, c=7;
б) a=4, b=3, c=-7; г) a=7, b=4, c=3.
7) Чему равно произведение корней уравнения 2x2+11x-14=0:
а) 14; б) -14; в) -7; г) 7.
8) Найдите коэффициент k для уравнения x2+kx-30=0, если один из корней равен -6.
а) 5; б) -5; в) 1; г) -1.
Тест.
2 в.
1) Выберите неполное квадратное уравнение из данных:
а) x2-1+x=0; в) 3x-2x2+1=0;
б) x-2x2+2=0; г) x2-2=0.
2) Какое из чисел является корнем уравнения –x2+2x+3=0?
а) 3; б) -2; в) 2; г) -3.
3) Решите уравнение 2x2-12x=0.
а) 6 и 0; б) 6 и -6; в) 0 и -6; г) 6.
4) Сколько корней имеет уравнение x2-2x+7=0?
а) множество; б) один; в) два; г) ни одного.
5) Решите уравнение 3x2-11x+8=0.
а) - 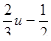 ; б) -
; б) - 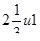 ; в)
; в) 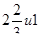 ; г)
; г) 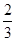 и-1.
и-1.
6) Укажите в квадратном уравнении x2+10x+21=0 его коэффициенты:
а) a= -1, b=10, c= -21; в) a= -1, b= -10, c= 21;
б) a=1, b= 10, c= 21; г) a= 1, b= -10, c 21.
7) Чему равно произведение корней уравнения x2-7x+10=0:
а) 10; б) -10; в) 5; г)-2.
8) Найдите коэффициент k для уравнения x2-3x-k=0, если один из корней равен -1.
а) 4; б) -4; в) 3; г) -3.
Задание 3. Повторение формул, терминологический диктант.
1в.
1. Формула нахождения дискриминанта квадратного уравнения.
2. Формула нахождения корней квадратного уравнения.
Вставьте пропущенные буквы.
Ко фф циент
Б кв дратное ур внение
Св бодный член
Р вносильное ур внение
Тр хчлен
Переме ная
Док зательство
2в.
1. Формула разложения квадратного трехчлена на множители.
2. Формула Виета.
Вставьте пропущенные буквы.
Д скр минант
Пр веденное ур внение
В ет Фр нсуа
Ир циональное ур внение
П раметр
А горитм
Т орема
Задание 4. Решение контрольной работы.
Контрольная работа.
1в.
1. Решите уравнения:
а) 2x2+7x-9=0;
б) 9x2+8=18x.
2. Разложите на множители квадратный трехчлен:
13x+3x2+14.
3. Сократите дробь:
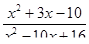 .
.
4. Решите уравнение:
(x-4)(x+4)=2x-16.
5. Решите биквадратное уравнение:
x4-10x2+9=0.
Контрольная работа.
2в.
1. Решите уравнения:
а) 7x2-9x+2=0;
б) 7x-4x2=-15.
2. Разложите на множители квадратный трехчлен:
а) 3x2-8x+6=0.
3. Сократите дробь:
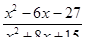 .
.
4. Решите уравнение:
(x-3)(x+12)=0.
5. Решите биквадратное уравнение:
x4-x2-12=0.
Приложение 15

Приложение 16

Приложение 17

Приложение 18
Дата: 2019-05-28, просмотров: 307.