Зачет как одна из форм контроля знаний
Учащихся по алгебре в 8 классе
Выпускная квалификационная работа
по специальности 050201 Математика
Шараповой Яны Николаевны
Специальность 050201
Математика
Группа М-51
отделение: очное
Руководитель: Л.Г. Янкина
преподаватель математики и методики математики
2008
Оглавление
Введение
Глава 1. Теоретические основы проверки знаний, умений и навыков на уроках математики
1.1 Методы контроля знаний, умений и навыков учащихся
1.2 Методика проведения зачетных уроков
Глава 2. Экспериментальная работа по изучению влияния уроков-зачетов по математике в 8 классе
2.2 Анализ аналитической работы по подготовке к эксперименту
2.3 Апробация и описание эксперимента
Заключение
Литература
Приложения
Введение
Обучение – это целенаправленный процесс передачи общественно-исторического опыта, организация усвоения знаний, умений и навыков [2].
Для обучения большое значение имеет установление уровня обученности школьников – уровня определенных стандартов необходимых знаний, для того чтобы была непрерывная система образования, нужно проверять и оценивать знания и умения своих учеников по всем пройденным темам и разделам. Опрашивать их по изученному материалу, проводить письменные проверочные работы, диктанты, тестирования, а также и зачетные уроки. Далее оценивать результаты проверки в баллах или оценочных суждениях.
Учителю контроль знаний позволяет определить уровень усвоения учебного материала по математике и в случае необходимости провести их коррекцию, ученику – привести в систему усвоенной за определенное время учебный материал, обобщить его, выделить главное, с акцентировать на нем внимание, скорректировать в случае необходимости отдельные знания и в оценке и отметке увидеть результаты своей деятельности.
Диагностировать, контролировать, проверять и оценивать знания и умения учащихся по математике нужно последовательно, согласно порядку изучения математического материала. Тематический контроль знания учащихся по математике является одним из основных условий повышения качества обучения. Умелое владение учителем различными формами контроля знаний способствует повышению заинтересованности учащихся в изучении предмета математики, предупреждает отставание, обеспечивает активность учащихся на занятиях.
С целью тематического контроля за уровнем обучения в ходе учебного процесса учителю целесообразно выбрать такую систему контроля, как зачет. От стандартных форм контроля зачетная система отличается по характеру проведения. Зачет – это специальный этап контроля, целью которого является проверка достижения учащимися уровня обязательной подготовки.
Однако задачу такого урока не следует ограничивать только осуществлением функций контроля, урок должен и обучать учащихся – совершенствовать их знания, умения и навыки. Проверке подвергается основное из пройденного по части темы, по учебной теме в целом. При этом контроль не должен быть односторонним – проверять следует как сами знания, так и умения их применять. Лучших результатов достигаются те учителя, которые ориентируются в первую очередь на проверку уровня развития учащихся, а не на проверку их памяти.
Проблемой необходимости проверки знаний, умений и навыков учащихся по математике занимаются многие педагоги и научные работники в области дидактики: Ю.Я. Яковлев, В.А.Оганесян, Ю.М.Колягин, А.В.Соколова, В.В.Пикан и другие [2].
В своих трудах они рассмотрели теоретические вопросы проверки знаний, умений и навыков учащихся старших классов. В педагогической литературе мало освещается проблема введения зачетной системы.
В периодических изданиях, журналах и газетах время от времени можно найти небольшие статьи, посвященные зачетной системе проверки знаний, умений и навыков.
Публикации, посвященные вопросу использования различных форм контроля можно найти в газетах «Математика» и в журнале «Математика в школе».
Они знают представление о применении тестирования, математических диктантов и тематических зачетов в 8 классе. Однако все эти публикации появляются нерегулярно.
Данная тема заслуживает должного внимания, так как без прочного усвоения знаний детьми невозможно дальнейшее обучение, а уровень усвоения знаний можно увидеть с помощью проведения комплексной проверки знаний, умений и навыков учащихся. В этом помогают проведение зачетных уроков.
Цель исследования: выявить зависимость качества образования от зачетной формы контроля знаний на уроках алгебры в 8 классе.
Объект исследования: процесс обучения математике учащихся 8 класса.
Предмет исследования: педагогические условия проведения зачетных уроков с использованием различных форм проверки знаний, умений, навыков учащихся по алгебре 8 класса.
Контингент: учащиеся 8 класса.
Задачи исследования:
- Проанализировать методическую литературу по данной теме;
- Изучить разные формы проверки знаний, умений и навыков на зачетном уроке;
- Разработать и апробировать зачетные уроки в 8 классе.
Гипотеза: если на уроках алгебры в 8 классе систематически использовать зачетную форму контроля учебных достижений школьников, то это положительно скажется на качестве их знаний в данной предметной области.
Устная работа
Наиболее хорошим методом проверки знания фактического материала и качества мышления школьника является устный опрос.
При проведении устного опроса учитель стремится проверить, насколько учащиеся овладели учебным материалом, и, кроме того, вовлечь, по возможности всех учащихся в активную работу. Все это можно выяснить, слушая ответ ученика [8].
Важное значение имеет устный опрос для развития математической речи учащихся: ведь это чуть ли не единственный вид речевой практики ученика на уроке. Для решения этой задачи большое значение имеет характер заданий и вопросов учителя. Следует чаще предлагать вопросы, требующие объяснения: объясни, как ты решил эту задачу, это уравнение.
Полезно включать задания на сравнение: сравни решение примеров, сравни эти трапеции и т. д. Сознательно ли усвоен материал — помогают выявить нетрафаретные задания, особенно задания к решению жизненных задач (сравнить площадь пола в классе и коридоре и т. п.).
При устном опросе дети высказывают свою мысль. Нужно учить высказываться, грамотно оформлять свою мысль. При рецензии ответа используется схема:
-все ли существенное освещено в рассказе;
-сумел ли ученик добавить что-либо к учебнику;
-насколько последовательно изложил рассказ;
-аргументированы ли умозаключения;
-правильно ли сделан вывод;
-оценить речь учащегося.
Ученики к ответу должны готовиться по схеме (по плану):
-главная мысль;
-аргументы для ее развития;
-вывод.
Устный опрос позволяет обстоятельно выяснить знания учащиеся, однако он требует много времени, что ограничивает возможность проверить большое количество учащихся. Кроме того, в устном опросе вопросы учителя и ответы учащихся нигде не фиксируются. Это мешает учителя возможности сравнивать ответы разных учащихся на один и тот же вопрос, ответы оного и того же ученика, данные в разное время учебного года. Но, несмотря на эти недостатки, устный опрос - исключительно ценный элемент урока, если его структура проработана в деталях [8].
Проводя любой вид опроса учитель обязан создать такую психологическую обстановку опроса, при которой отвечающий ученик чувствовал бы себя совершенно спокойно, непринужденно, бодро, чтобы его ничто не нервировало, не подавляло, не мешало. Только при этом условии возможно объективное, полное и глубокое выявление истинных знаний учащегося и, справедливая оценка, которую он должен получить.
Следовательно, устный опрос важный этап урока - зачета, так как проверяются не только знания, но и формируется математическая речь.
Фронтальный опрос – это, в сущности проверочная беседа учителя с классом. Учитель задает классу вопросы, отдельные учащиеся коротко отвечают на них [18].
Обычно прибегают к проверочной беседе тогда, когда не предполагается специально оценить знания учащихся, но необходимо восстановить в их памяти те или иные явления, закономерности, определения. Нередко учителя и эту форму проверки знаний используют для учета успеваемости, так называемый балл составляется из совокупности всей работы ученика на уроке, в том числе и из ответа на проверочной беседе. Это определенным образом повышает ответственность учащихся, дисциплинирует их. Проставление оценок за активное участие в проверочной беседе возможно при условии, что ответы учащегося дают достаточное основание для определенного вывода. Одной из проблем фронтального опроса является недопонимание смысла проверочной беседы. Ее иногда проводят только затем, чтобы не упрекнули, что на уроке отсутствовал опрос. В результате проверочная беседа превращается просто в беглый опрос по самым разнохарактерным и случайным вопросам «прошедшего, предпрошедшего и давно прошедшего». Вопросы в этом случае логически никак не связаны, никакой цельной картины знаний учащихся не выясняют. Пользы в таком опросе, конечно, немного.
Подготавливая проверочную беседу с классом, надо совершенно отчетливо представлять себе, с какой конкретной целью она предпринимается. В главном назначении проверочной беседы является подведение прочного фундамента под усвоение материала, который предстоит изучать учащимся. Поэтому ее обычно и проводят перед изучением нового материала.
Письменная работа
Кроме устного ответа, широко применяется методом проверки знаний учащихся, метод письменных работ, письменная проверка.
Письменные работы имеют огромное значение и большой успех, так как:
- гораздо объективнее, чем в устном ответе выявляются состояния знаний каждого ученика;
- позволяет проверить знания темы сразу у всех учащихся;
- дают возможность увеличить число проверок знаний каждого ученика;
- четко показывают учителю характер отдельных недочетов в знаниях учащихся;
- требуют от учащихся большой точности и самостоятельности в выражении своих знаний;
- усиливают в учащихся чувство ответственности за результат работы [19].
Письменные проверочные работы полезно проводить без специальной подготовки к ним учащихся. Это позволяет объективно проверить прочность усвоения знаний учащимися и предохраняя учащихся от возможной перегрузки домашними учебными заданиями дни, предшествующие письменным проверочным работам, перегрузки, которая происходит от того, что учителя перед этими работами заставляют учащихся специально повторять к ним соответствующий материал. Проведение письменных проверочных работ без специальной подготовки уменьшает волнение учащихся, что очень существенно для объективности проверки.
Таким образом, письменная проверка является одним из важных методов контроля и оценки знаний, умений и навыков учащихся.
Для оперативного контроля знаний и умений по математике учеников средней школы в последние годы в России широко используются тесты [6].
Главное достоинство тестовой проверки в скорости, но работа по созданию тестов их эффективности достаточно сложная и долгая.
Анализ научной литературы позволяет выделить два основных вида тестов: психологические (тесты интеллекта) и педагогические (тесты достижений или тесты успешности). Подробнее рассмотрим тесты достижений. Тесты достижений использовались на различных этапах процесса обучения математике: усвоение новых знаний, формирование умений и навыков, обобщение и систематизация знаний и др. Выступая как инструмент оценивания, тесты достижений, тем не менее, имеют значительные отличия от контрольных работ.
Во-первых, тесты - объективный и более качественный способ оценивания и, во-вторых, показатели тестов ориентированы на измерение степени и определение уровня усвоения ключевых понятий, тем, разделов учебной программы, умений и навыков учащихся. Контрольные работы ориентированы лишь на констатацию наличия у учащихся определенной совокупности формально усвоенных знаний [17].
Хорошо известно, что одним из методов проверки состояния обученности учащихся являются итоговые письменные контрольные работы различных видов [25].
При разработке содержания контрольной работы необходимо правильно определить ее цели с точным учетом времени проведения. При этом очень важно учитывать момент процесса обучения, в который проводится контрольная работа. Помня, что процесс овладения умениями, навыками - длительный. Из этого следует, что подход к определению целей проведения работы должен быть продуманным и осторожным.
Каждая итоговая контрольная работа проводится по окончании изучения темы. К концу изучения темы, с одной стороны, остаются недоработанными еще какие-то вопросы, а с другой стороны, в ходе работы над этой темой продолжалось закрепление, отработка и совершенствование навыков, приобретавшихся еще при изучении предыдущих тем.
В итоговых проверках выявляются такие качества знаний учащегося, как прочность осознанность, оперативность, которая предполагает способность ученика применить одно и тоже умение в ходе решения задач различного содержания. Итоговый контроль нацеливает учащегося на долгосрочное усвоение важнейшего материала, а учителю дает возможность проверить прочность овладения опорными умениями и навыками.
При определении цели проведения контрольной работы необходимо учитывать реальный момент процесса обучения и избегать постановки непостижимых целей. Цель проверки состоит не в том, чтобы «поймать» ученика на чем-то, а в том, чтобы убедиться, что дети действительно усвоили основные вопросы темы.
Определив цель, нужно продумать отбор знаний, отвечающих цели. Приступая к составлению контрольной работы по теме, учителю целесообразно вернутся к началу изучения темы, восстановив в памяти с помощью учебника, методических рекомендаций, своих конспектов уроков все, чему он учил, что и на каком уровне должны были усвоить дети, составить примеры на каждый из изученных приемов, не упуская ни одного из них.
Наряду с определением цели отбором содержания контрольной работы немаловажен и выбор соответствующих форм организации контроля.
Не следует перегружать работу большим количеством заданий и нельзя гнаться за быстротой их выполнения. Это может отрицательно сказаться на результатах. Следует помнить, что цель проведения проверки в этом случае - не скорость выполнения вычислений и не максимальный объем однотипичных примеров, а знания алгоритма письменного вычисления и умения его применять [24].
Задания могут быть различным: это могут быть отдельные карточки с записанными на них примерами, на которых детям останется только написать ответ; можно провести проверку и в форме арифметического диктанта. Очень удобно использовать простейших перфокарт, которые накладываются на страницу тетради или лист бумаги, где пишут только ответы, располагая их в столбик, а перфокарты с примерами сохраняются для последующего использования.
Не исключается и комбинированная работа, когда часть примеров дается в описанной выше форме, а часть - в форме письменной работы ( в число заданий включаются те случаи, по которым формирование навыка только началось). Это будет рационально и интересно, но необычно.
Следует знать, что итоговая проверка может проводиться как в форме устного зачета, так и в форме обычной контрольной работы.
Из таблицы видно (приложение 1), что каждая из форм проверки имеет как свои плюсы, так и свои минусы. Если включить оба вида проверки знаний, умений и навыков в урок, то проверка будет более глубокой и полной. Оба вида проверки можно совместить в уроке-зачете.
Структура урока-зачета очень сложна, возникает очень много трудностей при подготовке и проведению, существует мало методик и рекомендаций для проведения данного типа проверки знаний. Для разработки зачетных уроков была изучена методика проведения зачетных уроков, выделены отрицательные и положительные стороны работы.
Заключение
Проверка знаний, умений и навыков, учащихся от условий проверки знаний зависит, прежде всего, от качества и форм проверяемого материала.
В данной работе был рассмотрен урок-зачет как одна из форм проверки знаний, умений и навыков учащихся.
В последние годы в теории и практике обучения математике вопрос об использовании зачетной системы в оценке уровня усвоения знаний становится все более актуальным.
Из выше проделанной работы можно сделать вывод, что применение зачетной системы контроля положительно сказывается на качестве знаний в данной предметной области, так как:
- проверка знаний есть форма закрепления, обязательное участие в зачете делает его более весомым, заставляет серьезнее относиться к подготовке, что положительно влияет на формирование необходимых умений и навыков;
- проверка знаний есть форма воспитания у учащихся навыков правильного воспроизведения своих знаний и умений, вооружения методикой такого воспроизведения. И тем лучше организован опрос, тем больше оснований надеяться, что учащиеся научаться отвечать так, как требуется;
- проверка знаний есть важная объективная форма самоконтроля учителя. Пробелы в знаниях выявляются именно во время зачета, что позволяет как учителю, так и самому ученику своевременно обратить на их внимание;
Работа носит исследовательский характер, выявление зависимости качества образования от зачетной формы контроля знаний на уроках алгебры в 8 классе, который включает анкетирование учителей математиков разных школ и экспериментальной части. Из работы можно сделать вывод, что в контрольном классе, котором не проводились зачетные уроки, знания остались на прежнем уровне. В экспериментальном классе, котором были проведены ряд зачетных уроков, повысился уровень знаний.
В ходе написания выпускной квалификационной работы по теме « Зачет как одна из форм контроля знаний учащихся по алгебре в 8 классе» были реализованы поставленные цели и задачи. Гипотеза дала положительный результат.
Таким образом, разнообразие форм проверки знаний и их сочетания в системе зачетного урока повышает эффективность усвоения учащимися учебного материала, так как при этом не только проверяется уровень усвоения знаний, и формируются многие навыки и умения, необходимые для дальнейшего обучения.
Выпускная квалификационная работа может стать методическим пособием для студентов Кунгурского педагогического училища, как при подготовке докладов, сообщений на эту тему, так и при проведении пробных уроков или преддипломной практики. А также ею могут воспользоваться учителя математики, преподающие в средней школе, стремящиеся повысить уровень знаний на уроках алгебры, используя для этого зачетные уроки.
Литература
1. Акимова, З.В. Зачет на каждом уроке / З.В.Акимова // Математика в школе. -1994. -№ 1. -С.10.
2. Арнольд, В.И. Математика и математическое образование в современном мире /В.И.Арнольд // Математическое образование, -1997. -№ 2. -С.20.
3. Бантова, М.А., Бельтюкова, Г.В. Методика преподавания математик в начальных классах /под ред. М.А.Бантовой. -3-е изд., испр. -М.:Просвещение, 2000. -С. 154.
4. Батурина, Г.И., Кузина, Т.Ф. Введение в педагогическую профессию: учеб.пособие для студ. сред.пед.уч.заведений /Г.И.Батурина. -М.:Изд.центр «Академия», 1999, -С. 154-155.
5. Бигельдинова, Б.Н. Взаимопроверки на уроках математики /Б.Н.Бигельдинова// Математика. -2001. -№ 10. -С.27-32.
6. Блинова, А.И. и др. Система тестов для математических классов /А.И.Блинова // Математика. -2002. -№ 13. -С. 13-15.
7. Богоявленский, Д.Н., Меченская, Н.А. Психология усвоения знаний в школе / Д.Н.Богоявленский. -М.: Изд-во АПНРСФСР, 1999. -С.345.
8. Быков, А.В. О технологии проведения зачетного урока / А.В.Быков // Математика в школе. -1998. -№ 5. -С.16.
9. Воскерчин, М.И. Об использовании метода тестов при учете успеваемости школьников /М.И.Воскерчин. -М.: Сов.педагогика, 2000. -534с.
10. Генкин, Г.З. Тематический контроль по планиметрии: Методические рекомендации /Г.З.Генкин.-М., 1993.-С.34.
11.Жохов, В.И. Преподавание математики в 5-6 классах. Методические рекомендации для учителя / В.И.Жохов. -М.: Мнемозина, 2000. -С.43 5. 12.3аруцкая, С. Обобщающее повторение / С.Заруцкая // Начальная школа. -2000.-№ 13.-С.5.
13.Зотов, Ю.Б. Организация современного урока / Ю.Б.Зотов. -М.: Просвещение, 2001. -С.102.
14.Иванова, Т. Примерное тематическое планирование / Т.Иванова // Математика. -2000. -№ 29, -С.1-20.
15.Из опыта преподавания математики в средней школе: Пособие для учителей / сост. А.В.Соколова. В.В.Пикан, В.А.Оганесян. -М.:Просвещение, 1999.-С.45.
16.Кабанова-Меллер, Е.Н. Психология формирования знаний и навыков у школьников /Е.Н. Кабанова-Меллер.-М.: Изд-во АПНРСФСР, 1999.-С.65.
17.Каменина, И.П., Ордынкина. И.С. Качественный анализ проверки знаний /
И.П.Каменина // Начальная школа. -2000. -№ 10. -С.95.
18. Каршакова, Л.Б., Чуйкова, Н.В. Московское математическое общество о перспективах школьного курса /Л.Б.Каршакова // Математика в школе. -2001.-№ 13.-С.13
19.Кобзева, А. Использование зачетной системы в оценке уровня усвоения знаний/А.Кобзева //Математика. -1999. -№ 18. -С.13-14.
20.Мартынова, Г. Применение нестандартных уроков в обучении математики /Г.Мартынова // Математика. -2001. -№ 25. -С.30-32.
21.Минина, Л. Тестовые задания /Л.Минина // Математика. -2001. -№ 29. С.5.
22.Никитина, В. Тематические зачеты /В.Никитина // Математика. -2001. -№10. -С.27-32.
23.Портнов, М.Л. Уроки начинающего учителя /М.Л.Портнов // Математика.-2002. -№ 7. -С.5.
24.Сухарский, А. Тематический контроль /А.Сухарский // Народное образование. -1999. -№ 12. -С.57.
25-Селевко, Г.К. Современные познавательные технологии /Г.К.Селевко. М.: 1998.
26-Темербекова, А.А. Методика преподавания математики /А.А.Темербекова.-М.:2003.-С.11б
Приложение 1
Сравнение устной и письменной проверки.
| Устная проверка | Письменная работа |
| «+» | «-« |
| Развивается математическая речь | Не развивается математическая речь |
| Умение выражать и высказывать свою мысль | Не выражают свои мысли |
| «-« | «+» |
| Нельзя проверить всех учащихся | За небольшое количество времени можно проверить знания всех учащихся |
| Не фиксируется проверка | Фиксируются проверка и результаты |
Приложение 2
Контроль и оценка результатов обучения в школе
Письмо Мин. общего и проф. образования от 19.11.98г. Методическое письмо разработано с учетом современных требований к деятельности учителя по контролю и оценке результатов обучения, реализует принципы гуманизации и индивидуализации обучения.
Требования к оцениванию
Прежде всего, необходимо учитывать психологические особенности ребенка младшего школьного возраста: неумение объективно оценить результаты своей деятельности, слабые контроль и самоконтроль, неадекватность принятия оцени учителя и др. Любая проверка знаний должна определяться характером и объемом ранее изученного материала и уровнем общего развития учащихся.
Не менее важно требование объективности оценки. Это проявляется прежде всего в том, что оценивается результат деятельности ученика. Личное отношение учителя к школьнику не должно отражаться на оценке. Это особенно важно потому, что нередко педагог делит детей на отличников, хорошистов, троечников и, невзирая на конкретный результат работы, ставит отметку в соответствии с этим делением: отличнику оценка завышается, а троечнику - занижается.
Характер принятия школьниками оценки учителя зависит от степени сформированности у них самооценки. Реализация этого требования имеет особое значение в развитии учебно-познавательной мотивации ребенка и его отношения к учению. Отрицательной стороной деятельности учителя по контролю и оценке является его эгоцентричность.
Он стоит как бы над детьми, только сам имеет право оценить, похвалить, исправить ошибки, пожалеть, или усилить наказание. Ученик не принимает участия в этой деятельности. Более того, его участие часто наказывается («не подсказывай» - а он нашел у соседа ошибку;
«исправил» - а он у себя нашел ошибку...). Такой подход формирует у школьника убеждение в том, что оценка - проявление отношения учителя не к его деятельности, а к нему самому.
Учителю следует помнить, что одним из основных требования к оценочной деятельности является формирование у школьников умений оценивать результаты, сравнивать их с эталонными, видеть ошибки, знать требования к работам разного вида. Работа учителя состоит в создании определенного общественного мнения в классе, каким требованиям отвечает работа на «отлично», правильно ли оценена эта работа, каково общее впечатление от работы, что нужно сделать, чтобы исправить эти ошибки? Эти и другие вопросы - становятся основой коллективного обсуждения в классе и помогают развитию оценочной деятельности школьников.
Приведем пример. Учитель проводит диктант, перед сдачей предлагает его проверить. Ученик находит в своей работе ошибки и исправляет их сам. В соответствии с инструкцией учитель снижает оценку на балл. Проанализируем эту ситуацию. Ученик сам нашел ошибки, что означает наличие у него навыка самоконтроля. Естественно, в данном случае требуется не наказание, а поощрение. Но найдется учитель, который скажет: «Ученик должен сразу же писать без ошибок». Однако процесс перехода умения в навык (а именно этого требует педагог) достаточно трудный и неровный, поэтому тот факт, что умение еще не может сразу применить правило написания, скорее его беда, а не вина. И пока у школьника не сформирован тот или иной навык, он должен иметь право на исправление ошибки, на совместный с педагогом анализ причин своих неудач. Кроме того, непедагогична эта ситуация еще и потому, что у школьника формируется негативное отношение к действию самоконтроля, безразличное отношение к оцениванию («Зачем искать у себя ошибки, если учитель все равно снизит отметку?»). Противоречие, образующееся при такой ситуации, отрицательно отражается на всем учебно-воспитательном процессе, так как вносит дискомфорт в отношения между обучаемым и обучающим, между одноклассниками, детьми и родителями.
В процессе реализации воспитательной функции создаются условия для формирования тех качеств личности, которые становятся стимулом положительного отношения к учению. Это касается прежде всего умения и желания осуществлять самоконтроль. Сюда относятся: умение сравнить результат своей деятельности с эталоном; умение анализировать правильность (неправильность) выбора способа учебного действия, средств достижения цели, поиск ошибок в чужой и своей работах, анализ их причин и определение путей исправления.
Таким образом, система контроля - оценочная основа обучения становится регулятором отношений школьника и учебной среды. Ученик превращается в равноправного участника процесса обучения. Он не только готов, но стремится к проверке своих знаний, к установлению того, чего он достиг в обучении, а что ему еще предстоит преодолеть.
Учитель применяет для оценивания цифровой балл (отметку) и оценочное суждение.
Оценивание устных ответов
В основу оценивания устного ответа учащегося положены следующие показатели:
правильность, обоснованность, самостоятельность, полнота.
Ошибки:
- неправильный,ответ на поставленный вопрос;
- неумение ответить на поставленный вопрос или выполнение задания с помощью учителя;
- при правильном выполнении задания неумение дать соответствующие объяснения. Недочеты:
- неточный или неполный ответ на поставленный вопрос;
- при правильном ответе неумение самостоятельно или полно обосновать и проиллюстрировать его;
- неумение точно сформулировать ответ решенной задачи;
- медленный темп выполнения задания, не являющийся индивидуальной особенностью школьника;
- неправильное произношение математических терминов.
Особенности организации контроля по математике
Текущий контроль по математике можно осуществлять как в письменной, так и в устной форме. Письменные работы для текущего контроля рекомендуется проводить не реже 1 раза в неделю в форме самостоятельной работы или математического диктанта. Желательно, чтобы работы для текущего контроля состояли из нескольких однотипных заданий, с помощью которых осуществляется всесторонняя проверка только одного определенного умения (например, умения сравнивать натуральные числа, умения находить площадь прямоугольника и др.).
Тематический контроль по математике в начальной школе проводится в основном в письменной форме. Для тематических проверок выбираются узловые вопросы программы:
приемы устных вычислений, действия с многозначными числами, измерение величин и др.
Среди тематических проверочных работ особое место занимают работы, с помощью которых проверяются знания табличных случаев сложения, вычитания, умножения и деления. Для обеспечения самостоятельности учащимся подбирается несколько вариантов работы, каждый из которых содержит 30 примеров (соответственно по 15 на сложение и вычитание или умножение и деление). На выполнение такой работы отводится 5-6 минут урока.
Итоговый контроль по математике проводится в форме контрольных работ комбинированного характера (они содержат арифметические задачи, примеры, задания геометрического характера и др.). В этих работах сначала отдельно оценивается выполнение задач, примеров, заданий геометрического характера, а затем выводится итоговая отметка за всю работу.
Приложение 3
Приложение 4
Билет № 1.
1) Параллелограмм (определение). Его св-ва (сформулировать все и доказать одно свойство).
2) Квадратный трехчлен (определение). Теорема о разложении кв. трехчлена на множители.
Билет М 2.
1) Параллелограмм (определение). Его признаки (сформулировать все и доказать один признак).
2) Теорема Виета (доказательство). Теорема обратная теореме Виета (формулировка)
Билет № 3.
1) Прямоугольник (св-ва, определение, признак). Св-во диагоналей прямоугольника (Доказать)
2) Решение неполных кв. уравнений.
Билет № 4.
1) Ромб (определение, св-ва). Доказать св-ва диагоналей ромба.
2) Вывод формул корней кв. уравнения.
Билет № 5.
1) Определение прямоугольника. Теорема о площади прямоугольника.
2) Решение кв. уравнений со вторым четным коэффициентом.
Билет № 6.
1) Определение параллелограмма. Теорема о площади параллелограмма.
2) Множество действительных чисел.
Билет № 7.
1) Определение треугольника. Теорема о площади треугольника (^=1\2а На)
2) Определения кв. корня из неотрицательного числа. Св-ва кв. корня (записать все равенства). Доказательство теоремы о кв. корне из произведения.
Билет № 8.
1) Определение трапеции. Теорема о площади трапеции.
2) Определение кв. корня из неотрицательного числа. Доказательство теоремы о кв. корне из частного.
Билет № 9.
1) площадь выпуклого четырехугольника с взаимно перпендикулярными диагоналями. Площадь ромба и квадрата (Формулы)
2) Функция у=^х. Ее график, св-ва.
Билет № 10.
1) Теорема Пифагора (Доказательство). Теорема обратная теореме Пифагора (формулировка)
2) построение графиков функций у=Г(х+Ь), у=цх)+а, у=Г(х+Ь)+а, у=-цх), если известен график функций у^х).
Билет № 11.
1) зт, со5,1§, с1§ острого угла в прямоугольном треугольнике. Нахождение их значения для угла 30°.2) функция у=к\х (к>0), ее график и св-ва.
Билет № 12.
1) зт, со8,1§, с1§ острого угла в прямоугольном треугольнике. Нахождение их значения для угла 45°
2) функция у=к\х (к<0), ее график и св-ва.
Билет № 13.
1) 8т, со8, \%, с1§ острого угла в прямоугольном треугольнике. Нахождение их значения для угла 60°
2) функция у=ах (а>0), ее график и св-ва.
Билет № 14.
1) определение подобных треугольников, признак подобия треугольников (формулировка всех и доказательство одного из них).
2) функция у=ах2 (а<0), ее график и св-ва.
Билет № 15.
1) определение средней линии треугольника. Теорема о средней линии треугольника.
2) Теорема о графике функций у=ах2 + вх + с, алгоритм построения его.
Билет №16.
1) Касательная к окружности (определение, св-ва, признаки). Доказательство теоремы св-ве касательной к окружности.
2) Алгебраические дроби, основное св-во, сложение и вычитание алгебраических дробей
Билет №17.
1) Вписанный угол, теорема о вписанном угле.
2) Алгебраические дроби, умножение и деление алгебраических дробей, возведение их в степень.
Приложение 5
Срезовый тест по алгебре
1. Разложите на множители:
1. x2y2-16z2
а) (xy-yz)2 в) (xy-4z)(xy+4z)
б) (x-y-16z)2 г) (xy-16z)(xy+16z)
2. 1+6m+9m2
а) не разлагается на множители в) (3m-1)2
б) (3m+1)(3m-1) г) (3m+1)2
3. 25a2-10a+1
а) (5a-1)2 в) (5a-1)(5a+1)
б) (5a+1)2 г) не разлагается на множители
4. m3-27
а) (m-3)(m2+3m+9) в) (m-3)(m2+6m+9)
б) (m+3)(m2-3m+9) г) (m+3)(m2-6m+9)
5. 1+8b3
а) (2b-1)(4b2-2b+1) в) (1-2b)(4b2-2b+1)
б) (2b+1)(4b2-2b+1) г)(2b+1)(4b2+2b+1)
6. Какое из равенств верно (да), какое неверно (нет)
1. 4x2-12xy2+9y2=(2x-3y2)2
2. m2+8mn+4n2=(m+2n)2
а) 1. да 2. нет в) 1. да 2. нет
б) 1. нет 2. нет г) 1. нет 2. да
7. Вычислите: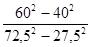 
а) -1 б) 1 в) -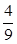 
г) 
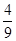
Приложение 6
Приложение 7
Приложение 8
Приложение 9
Приложение 10
Приложение 11
Приложение 12
Приложение 13
Приложение 14
Приложение 15
Приложение 16
Приложение 17
Приложение 18
Приложение 20
Приложение 21
Итоговая контрольная работа
1. Решите уравнение:
.
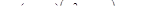
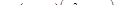2. Решите уравнение:
.
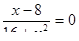
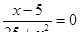3 Дана функция y=f(x), где f(x)=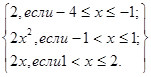 
.
4. Решите графически систему 
.
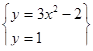5. Решите уравнение:
(x-4)(x+4)=2x-16.
6. Расположите числа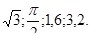 
в порядке возрастания.
Зачет как одна из форм контроля знаний
Дата: 2019-05-28, просмотров: 246.
