Определим устойчивость САР температуры в теплице. Для этого воспользуемся любой из полученных в предыдущем пункте передаточных функций, из которых следует, что характеристическое уравнение системы:
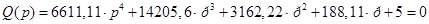
Для анализа устойчивости воспользуемся условиями устойчивости для уравнения четвертой степени:
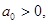
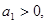
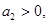
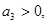
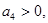
Все коэффициенты характеристического уравнения положительны.
Проверяем второе условие:
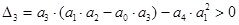
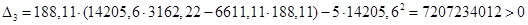
Полученный результат показывает, что система устойчива.
Анализ устойчивости по критерию Найквиста
Этот критерий основан на использовании амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы. Разомкнем систему и запишем передаточную функцию:
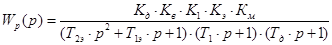
Все звенья разомкнутой системы устойчивы, поскольку одно звено имеет второй порядок, два звена - первый порядок и коэффициенты их характеристических уравнений положительны. 
Частотная передаточная функция разомкнутой системы:
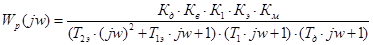
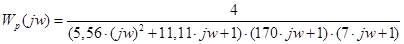
Для построения АФЧХ разомкнутой системы представим частотную передаточную функцию в виде:
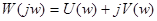 , тогда
, тогда
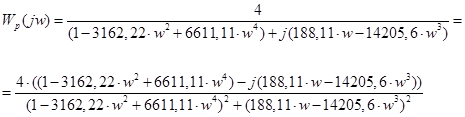 , получаем:
, получаем:
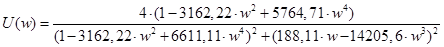
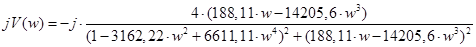
По этим выражениям, придавая  значения от 0 до ∞, строим на комплексной плоскости АФЧХ разомкнутой системы.
значения от 0 до ∞, строим на комплексной плоскости АФЧХ разомкнутой системы.
Таблица 2. - Результаты расчёта.
| w | 0 | 0,005 | 0,01 | 0,015 | 0,02 | 0,03 | 0,04 |
| U (w) | 4 | 2,13 | 0,69 | 0,15 | -0,08 | -0,24 | -0,27 |
| jV (w) | 0 | -2,17 | -1,89 | -1,43 | -1,09 | -0,68 | -0,44 |
Определим запасы устойчивости
Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины - запас устойчивости по фазе ∆φ и запас устойчивости по амплитуде ∆А. При проектировании САУ рекомендуется выбирать ∆φ≥30º и ∆А≥1. Для нашей САР температуры в теплице ∆φ=73º и ∆А=0,86, что удовлетворяет рекомендуемым величинам запасов устойчивости по фазе и амплитуде. Следовательно, это показывает, что наша система устойчива.
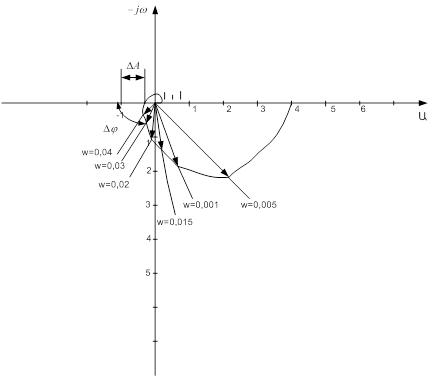
Рисунок 3. АФЧХ системы.
Анализ зависимости статической ошибки системы от изменения управляющего воздействия на систему
При выполнении такого анализа используют передаточную функцию системы для ошибки по управляющему воздействию.
Воспользуемся передаточной функцией для ошибки по управляющему воздействию, полученной ранее:
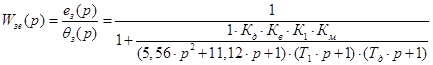
В статике р обращается в ноль, поэтому
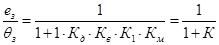 ,
,
где К - коэффициент передачи разомкнутой системы.
Таким образом, 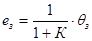
После подстановки численного значения К получаем 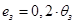 .
.
Рассматриваемая система имеет статическую ошибку, пропорциональную изменению управляющего воздействия на систему.
Из выражения для статической ошибки следует что величина статической ошибки тем меньше, чем больше коэффициент передачи разомкнутой системы.
Дата: 2019-04-23, просмотров: 294.