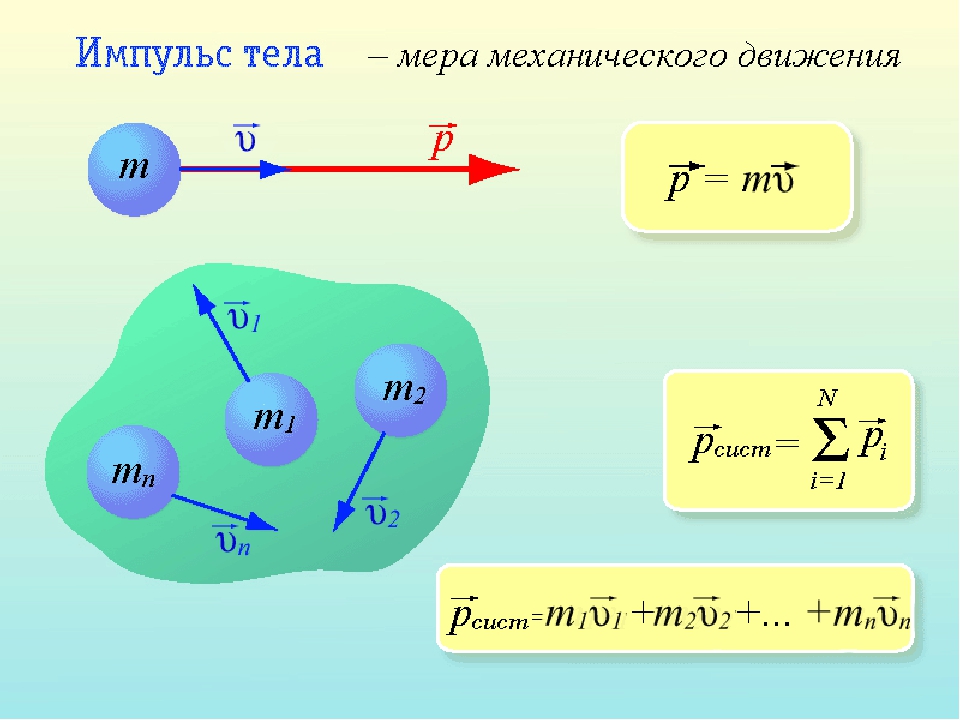
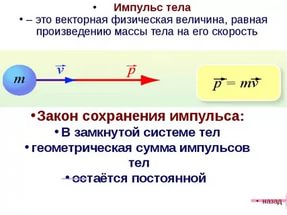
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является кг·м/с. Направление импульса тела совпадает с направлением скорости движения тела.

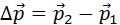Изменение импульса тела

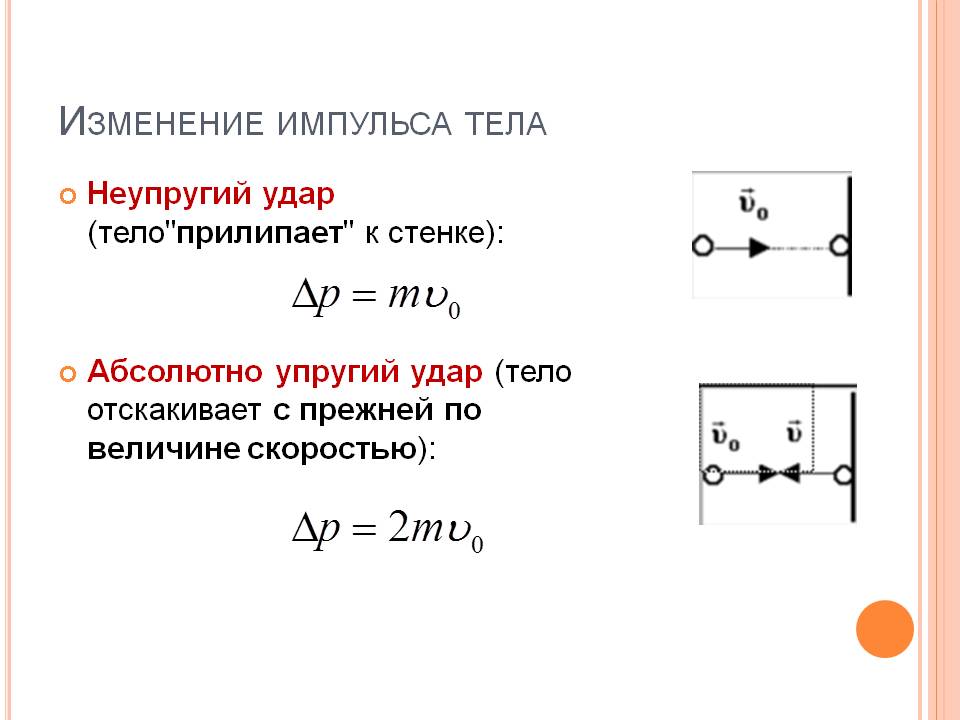
При абсолютно неупругом ударе                          при абсолютно упругом ударе                                                                                                                                       

Δ p = mυ ₀                                                        Δ p = 2 mυ ₀

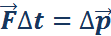  Импульс силы – векторная физическая величина, которая одновременно учитывает влияние модуля, направления и времени действия силы на изменение состояния движения тела.

· Вектор изменения импульса тела Δ p направлен по направлению действующей силы F

 Суммарный (полный) импульс системы тел – векторная сумма импульсов всех тел.

p = mυ₁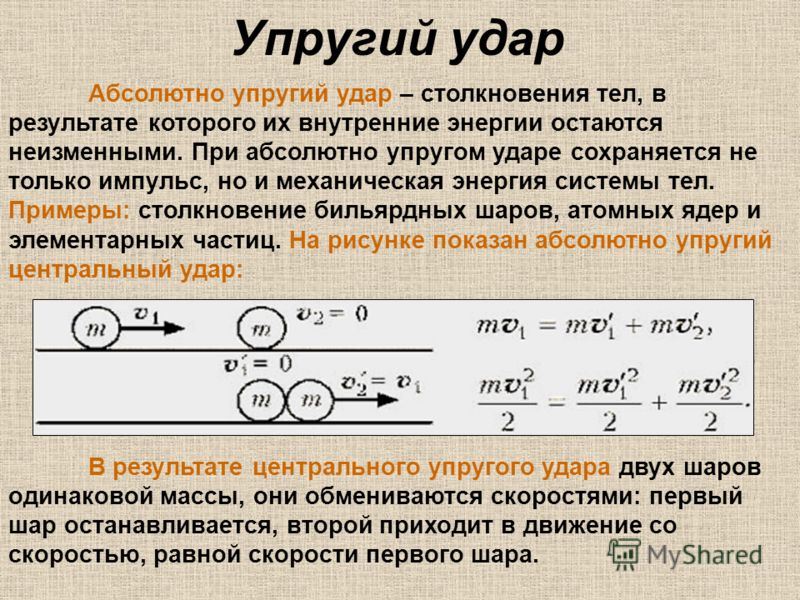                              

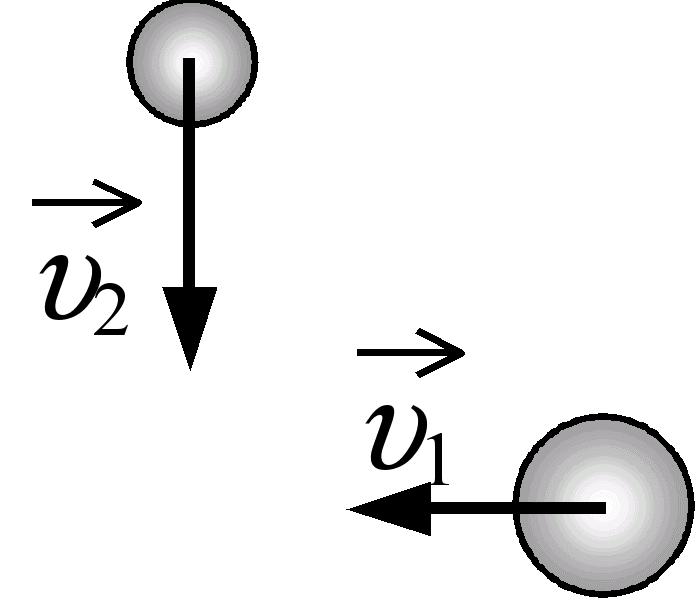
p = p₁ + p₂

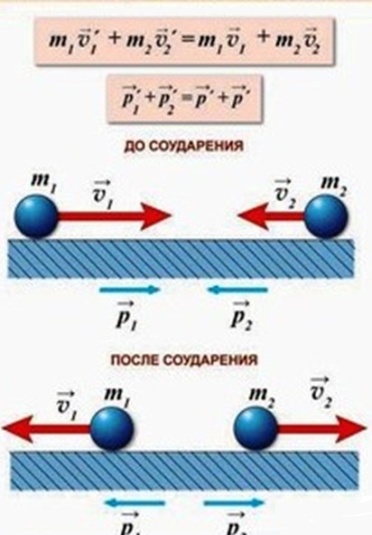                                                                                            p = 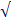 p₁² + p₂²

p = p₁ – p₂    

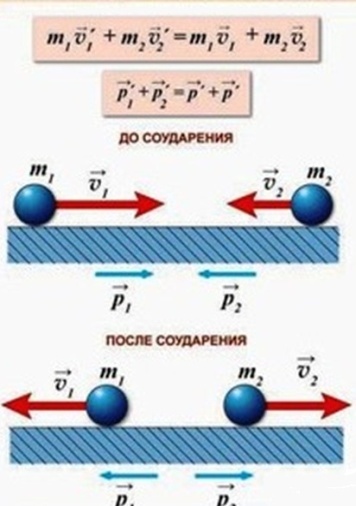p = p ₁ – p ₂

 Закон сохранения импульса: геометрическая сумма импульсов тел в замкнутой системе до взаимодействия равна сумме импульсов тел после взаимодействия       

Система тел называется замкнутой, если взаимодействующие между собой тела не взаимодействуют с другими телами.

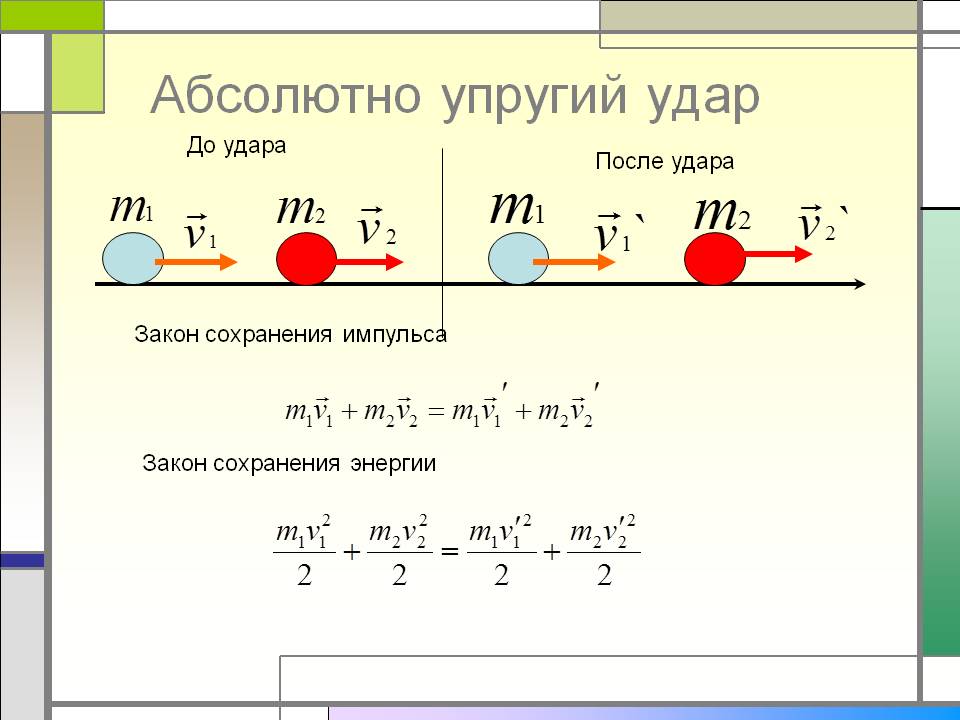
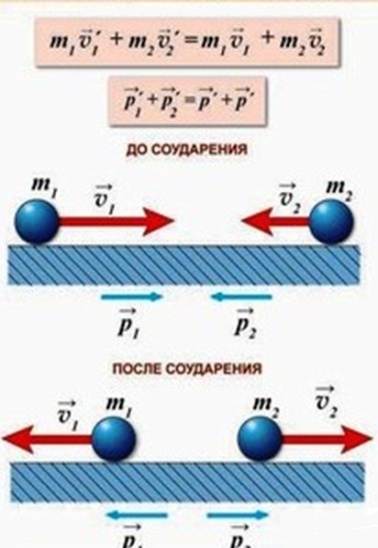
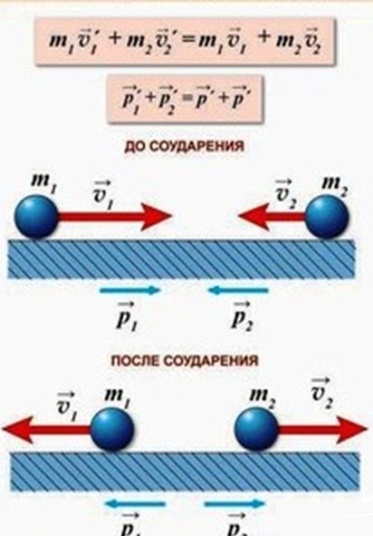 Упругое взаимодействие – столкновения тел, в результате которого они движутся в разные стороны, их внутренние энергии остаются неизменными. При абсолютно упругом ударе сохраняется не только импульс, но и механическая энергия системы тел.

· В результате упругого удара тела с одинаковой массой m₁ = m₂,  движущиеся навстречу друг другу, обмениваются скоростями

· Если шар, движущийся со скоростью υ_1, сталкивается с неподвижным шаром такой же массы, то первый шар остановится, а второй шар будет двигаться со скоростью υ₁.

Неупругий удар – столкновение тел, в результате которого они соединяются вместе и движутся дальше как единое целое.

При неупругом ударе часть механической энергии взаимодействующих тел переходит во внутреннюю, импульс системы сохраняется.

· При неупругом ударе тел, движущихся навстречу друг другу, скорость совместного движения тел будет направлена в сторону движения тела с большим импульсом.

 Механические колебания

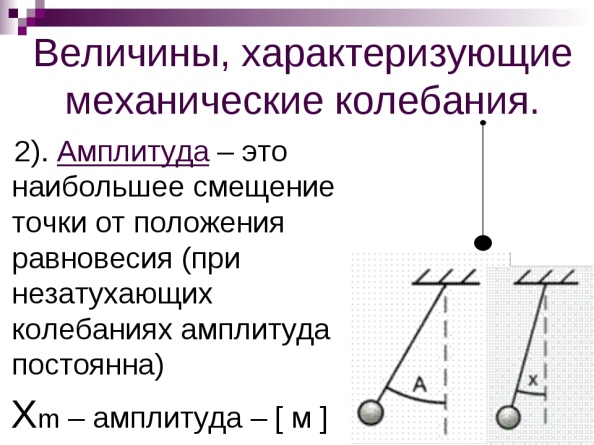Механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени. Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия. Период колебаний T — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды. Частота колебаний ν — это величина, обратная периоду: ν = 1/T. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону: x = A cos(ωt + α). Аргумент косинуса ωt+α называется фазой колебаний. Величина α, равная значению фазы при t = 0, называется начальной фазой. Начальная фаза отвечает начальной координате тела: x₀ = A cos α.

Величина ω называется циклической частотой.   Одному полному колебанию отвечает приращение фазы, равное 2π радиан: ωT = 2π, откуда ω = 2π/ T , ω = 2πν . Измеряется циклическая частота в рад/с (радиан в секунду).

· Путь, пройденный телом за 1 период, равен 4 амплитудам. S = 4A

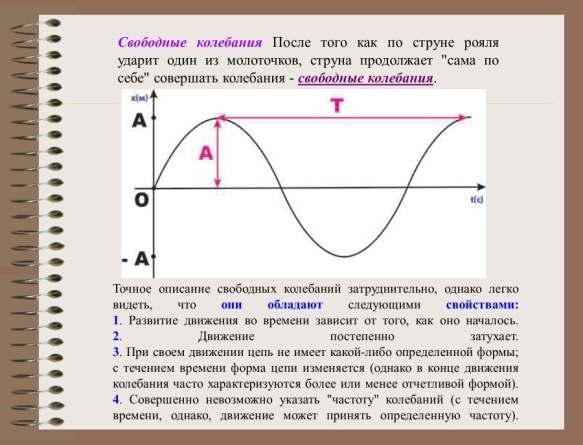
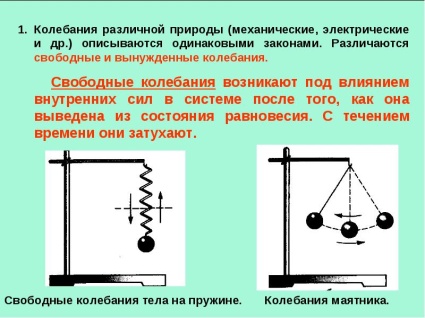
 Тело  совершает свободные колебания, если оно однократно выведено из положения равновесия и в дальнейшем предоставлено сама себе. Никаких периодических внешних воздействий  тело при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания,   нет.  

При отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует   трение, поэтому свободные колебания постепенно затухают.

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы F(t), периодически изменяющейся во времени (так называемой вынуждающей силы).

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити.   Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.   Циклическая частота колебаний математического маятника равна: ω= 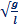.  Период колебаний математического маятника: T = 2π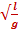

·  Период математического маятника не зависит от массы маятника и амплитуды колебаний.

· Чем короче длина маятника, тем меньше период колебаний.

·  T =2 π 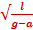 период маятника, движущегося вниз с ускорением а

· T =2 π 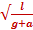 период маятника, движущегося вверх с ускорением а

· В невесомости математический маятник колебаться не будет, т.к сила тяжести равна нулю.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении Циклическая частота колебаний пружинного маятника, таким образом, равна: ω= 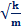   Отсюда и из соотношения T = 2π/ω находим период горизонтальных колебаний пружинного маятника: T = 2π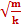    

· Если две пружины соединены параллельно, то k_общ =k₁ + k₂  ⇒ T = 2π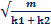

· Если две пружины соединяются последовательно, то 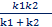    ⇒ T = 2π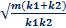

· Период пружинного маятника и на Земле, и в космическом корабле, летящем с постоянной скоростью, будет одинаков

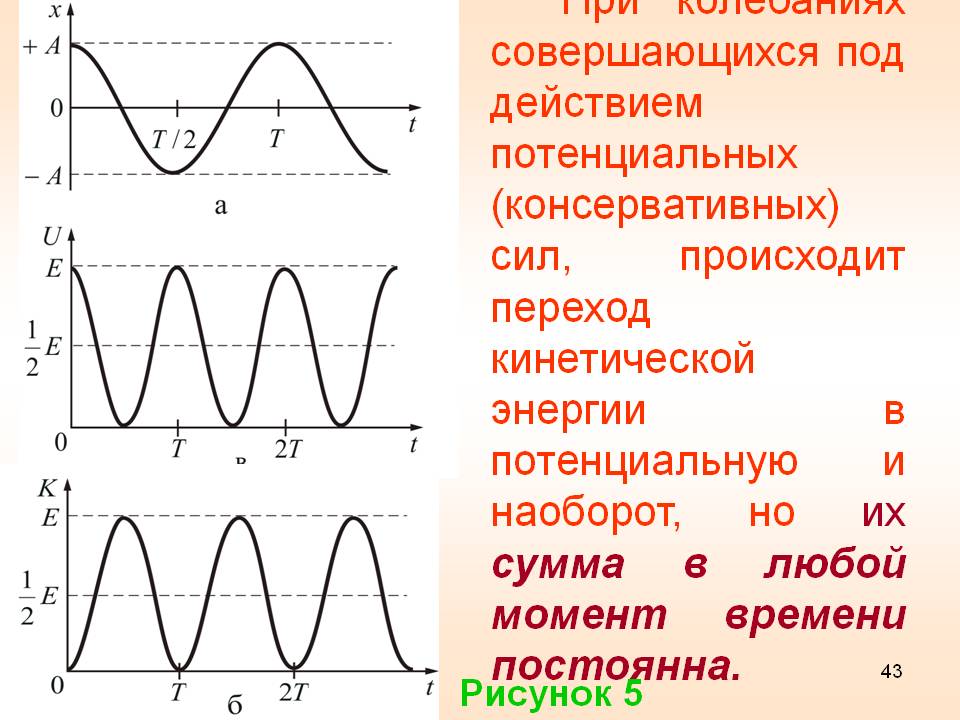Период колебаний энергии в два раза меньше периода колебаний координаты Т_эн =

Частота колебаний энергии в 2 раза больше частоты колебаний координаты ѵ_эн = 2ѵ_к

Полная энергия колебаний не зависит от времени, остаётся величиной постоянной Е = Е_к + Е_п = const

E = kx ² /2 + mυ ² /2 = kA ² /2 = mυ ² _мах /2

· Если нет сил трения и сопротивления, то полная энергия остаётся постоянной

· За период Е_к и Е_п 4 раза принимают равные значения.

· Через t = в первый раз Е_к = Е_п

· Период изменения энергии пропорционален периоду колебаний энергии, если период колебаний координаты увеличивается, то увеличивается период изменения энергии.

· Если пружина маятника всё время остаётся растянутой, то при движении груза вверх к положению равновесия потенциальная энергия в поле тяжести увеличивается (h- увеличивается), кинетическая энергия увеличивается (скорость увеличивается), потенциальная энергия пружины уменьшается (х – уменьшается)

· При движении вниз от положения равновесия скорость уменьшается ⇒ Е_к – уменьшается, высота уменьшается ⇒ Е_п – уменьшается, деформация пружины увеличивается, ⇒ Е_пруж увеличивается

· При движении вверх от положения равновесия скорость уменьшается ⇒ Е_к – уменьшается, высота увеличивается ⇒ Е_п – увеличивается, деформация пружины уменьшается ⇒ Е_пруж – уменьшается