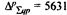Анализ динамики уровней качественных показателей по нескольким единицам означает анализ динамики уровней средних величин различных экономических показателей (средней себестоимости, средней цены, средней заработной платы и т. д.). Этот анализ выполняется с помощью системы взаимосвязанных индексов: индекса переменного состава, индекса фиксированного состава и индекса влияния структурных сдвигов.
Построение этой системы индексов показано на примере анализа себестоимости одного вида продукции А, выпускаемой несколькими предприятиями фирмы.
Изменение себестоимости продукта А по фирме (по группе предприятий) определяется следующим индексом:
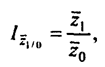
- средняя себестоимость единицы продукции по группе предприятии соответственно в отчетном и базисном периодах.
Средняя себестоимость единицы продукции в отчетном и базисном периодах исчисляется по формулам средней арифметической взвешенной:
- себестоимость единицы продукции каждого предприятия соответственно в базисном и отчетном периодах;
- выпуск продукции в натуральном выражении каждым предприятием соответственно в базисном и отчетном периодах.
Следовательно,
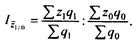
Этот индекс носит название индекса переменного состава. Это объясняется тем, что при исчислении средней себестоимости единицы продукции в отчетном периоде весами служило количество продукции отчетного периода. При определении средней себестоимости единицы продукции базисного периода весами было количество продукции базисного периода, т. е. исчислялись средние с меняющимися (переменными) весами.
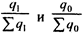
Величины отражают распределение продукции
по предприятиям, поэтому формула индекса себестоимости переменного состава может быть записана так:
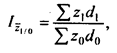
- удельный вес каждого предприятия в общем объеме выпуска продукта А соответственно в базисном и отчетном периодах.
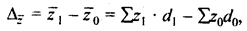
- абсолютное изменение средней себестоимости по группе предприятий.
Величина индекса переменного состава зависит от изменения уровня себестоимости по предприятиям и изменения в распределении физического объема продукции между предприятиями.
Чтобы устранить влияние изменений в структуре весов на показатель изменения уровня себестоимости, рассчитывается отношение средних с одними и теми же весами, т. е. исчисляется индекс себестоимости фиксированного состава. Для этого среднюю себестоимость определяют при структуре фактического объема продукции в текущем периоде.
Формула индекса себестоимости фиксированного состава записывается так:
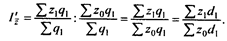
Полученный индекс себестоимости фиксированного состава отражает изменение уровня средней себестоимости в связи с изменениями значений себестоимости по отдельным предприятиям:
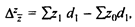
- абсолютное изменение средней себестоимости по группе предприятий за счет изменения уровня себестоимости по предприятиям.
Индекс влияния структурных сдвигов в объеме продукции определяется по формулам
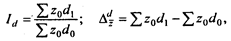
- абсолютное изменение средней себестоимости по группе предприятий за счет структурных сдвигов в объеме выпуска продукции.
Поскольку изменение средней себестоимости в целом по группе предприятий определяется изменением двух факторов, то
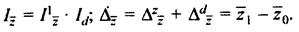
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Задача 1. Выпуск продукции по заводу почвообрабатывающих машин за два квартала следующий:
|
Вид продукции
| Выпуск, шт. | Отпускная цена за шт., тыс. д.е | ||
| 1 кв. (q0) | 2 кв. (q1) | 1 кв. (p0) | 2 кв. (p1) | |
| Плуги навесные 2500 | 2610 4,8 5,4 | |||
| Плуги прицепные 3000 | 2950 7,1 7,6 | |||
| Культиваторы навесные 3600 | 3700 5,0 5,7 | |||
Определить:
1) изменение (в %) выпуска каждого вида продукции, а также изменение выпуска продукции в целом по предприятию;
2) изменение цен (в %) по каждому виду продукции и среднее изменение цен по всему ассортименту продукции;
3) абсолютное изменение общей стоимости продукции, выделив из общей суммы изменение за счет изменения количества продукции и за счет изменения цен.
Решение
Для характеристики изменения выпуска продукции в целом по предприятию исчисляется агрегатный индекс физического объема продукции:
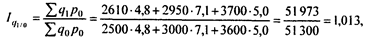
или 101,3%, т. е. в целом по предприятию выпуск продукции увеличился на 1,3%, в результате стоимость продукции увеличилась на 673 000 руб. (51 973 - 51 300).
Среднее изменение цен по всему ассортименту продукции определяется по формуле агрегатного индекса цен:
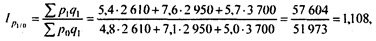
или 110,8%.
Таким образом, цены на продукцию предприятия повышены в среднем на 10,8%, за счет чего стоимость продукции повысилась на 5631 тыс. руб. (57 604-51 973).
3. Абсолютное изменение стоимости продукции определяется по формуле
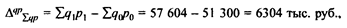
- абсолютное изменение стоимости продукции за счет изменения выпуска продукции
тыс. руб.;
- абсолютное изменение стоимости продукции за счет изменения цен;
|
|
тыс. руб;
что и соответствует ранее полученной цифре.
Задача 2. Определить, как изменились в среднем отпускные цены на продукцию, если количество произведенной продукции в отчетном периоде по сравнению с базисным увеличилось на 8,0%, а общая стоимость продукции уменьшилась на 5,0%.
Решение
Для определения индекса цен используется взаимосвязь между тремя индексами:
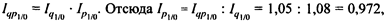
или 97,2%. Следовательно, отпускные цены на продукцию снижены в среднем на 2,8%.
6. ВОПРОСЫ К ЭКЗАМЕНУ (ЗАЧЕТУ) ПО СТАТИСТИКЕ
1. Современная организация статистики. Задачи органов статистики в условиях рыночных отношений.
2. Статистическое наблюдение. Основные организационные формы статистического наблюдения.
3. Виды статистического наблюдения.
4. Организация статистической отчетности. Специальные статистические наблюдения. Ошибки наблюдения.
5. Задачи группировок. Виды группировок: типологические, структурные, аналитические.
6. Группировочные признаки, их сущность и значение.
7. Важнейшие группировки и классификации, применяемые в статистике.
8. Ряды распределения. Их виды, назначение и использование.
9. Абсолютные величины и их значение в статистическом исследовании. Виды абсолютных величин, единицы измерения.
10.Виды относительных величин, способы их расчета и формы
выражения.
11.Виды средних и способы определения их величин.
12.Выборочное наблюдение - основные приема расчета ошибок.
13.Задачи статистического изучения вариации. Основные показатели
вариации.
14.Виды дисперсии. Правило сложения дисперсий.
15.Понятие о рядах динамики и их значение.
16.Основные правила построения рядов динамики.
17.Виды зависимостей между факторами. Показатели регрессии.
18.Аналитические модели зависимости между факторами.
19.Анализ рядов динамики.
20. Аналитические приемы обработки рядов динамики.
21.Понятие об индексах. Значение индексов в анализе социально-
экономических явлений.
22.Классификация индексов.
23.Индивидуальные и общие индексы.
24.Агрегатный индекс как основная форма общего индекса.
25.Средний арифметический и гармонический индексы.
26.Система взаимосвязей индексов.
27.Индексы постоянного, переменного состава и структурных
сдвигов.
28.Базисные и цепные индексы, их взаимосвязь.
Дата: 2019-05-28, просмотров: 214.
